REVIEW OF WAVE MECHANICS
... We can view all the other important equations concerning dynamical quantities in quantum mechanics from a similar perspective. Each dynamical variable is represented by an operator whose eigenvalues are the possible results of measurements of this dynamical variable. For example, measuring the energ ...
... We can view all the other important equations concerning dynamical quantities in quantum mechanics from a similar perspective. Each dynamical variable is represented by an operator whose eigenvalues are the possible results of measurements of this dynamical variable. For example, measuring the energ ...
Higher Order Gaussian Beams
... equation. We then plug in a suitable trial function (ansatz) and work to obtain a solution. ...
... equation. We then plug in a suitable trial function (ansatz) and work to obtain a solution. ...
IOSR Journal of Applied Physics (IOSR-JAP)
... In Newton’s theory of gravitation, gravitational force is assumed to be an action at a distance, implying that it can propagate instantaneously from one body to another. This assumption is in conflict with the special theory of relativity, according to which no interaction can propagate with a speed ...
... In Newton’s theory of gravitation, gravitational force is assumed to be an action at a distance, implying that it can propagate instantaneously from one body to another. This assumption is in conflict with the special theory of relativity, according to which no interaction can propagate with a speed ...
NMR SPECTROSCOPY
... 4) A Fourier transform is performed on the FID to produce an NMR spectrum with each signal represented by a peak at its relative Larmor frequency which is the frequency with which it wobbles as it spins. This is actually done several times and the results are added to increase the signal to noise ra ...
... 4) A Fourier transform is performed on the FID to produce an NMR spectrum with each signal represented by a peak at its relative Larmor frequency which is the frequency with which it wobbles as it spins. This is actually done several times and the results are added to increase the signal to noise ra ...
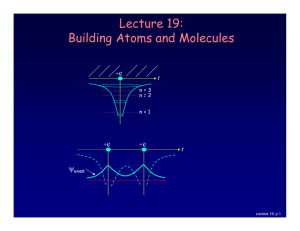
The Bohr model for the electrons
... We can predict the motion of a ball; But not an electron: problems locating small objects ...
... We can predict the motion of a ball; But not an electron: problems locating small objects ...
Lecture 17-PDF
... Similar to sodium atom, Hydrogen atom also shows doublet. Spectral lines of H found to be composed of closely spaced doublets. Splitting is due to interactions between electron spin s and the orbital angular momentum l Hα line is single line according to the Bohr or Schrödinger theory. occurs at 656 ...
... Similar to sodium atom, Hydrogen atom also shows doublet. Spectral lines of H found to be composed of closely spaced doublets. Splitting is due to interactions between electron spin s and the orbital angular momentum l Hα line is single line according to the Bohr or Schrödinger theory. occurs at 656 ...
Solutions - Illinois State Chemistry
... € and the population of the v=2 level is only 0.6% of the v=0 level. The intensity of a transition from an initial state to a final state is directly proportional to the population of the initial state. Thus, even though all the transitions mentioned, v=0→1, v=1→2, and v=2→3, are allowed by the sele ...
... € and the population of the v=2 level is only 0.6% of the v=0 level. The intensity of a transition from an initial state to a final state is directly proportional to the population of the initial state. Thus, even though all the transitions mentioned, v=0→1, v=1→2, and v=2→3, are allowed by the sele ...
Chapter 5
... Lowest energy to higher energy. Adding electrons can change the energy of the orbital. Half filled orbitals have a lower energy. ...
... Lowest energy to higher energy. Adding electrons can change the energy of the orbital. Half filled orbitals have a lower energy. ...