Download Studio Physics I

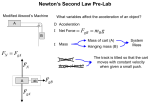
Studio Physics I
Design Activity #1-Forces and Motion in Coupled Systems
The Problem:
You are a volunteer in the city’s children’s summer program. One suggested activity is
for the children to build and race model cars along a level surface. To ensure that each
car has a fair start, your co-worker recommends a special launcher be built. The launcher
uses a string attached to the car at one end and (after passing over a pulley) the other end
of the string is tied to a mass hanging straight down. The car starts from rest and the
block is allowed to fall, launching the car along the track. After the block hits the
ground, the string no longer exerts a force on the car but the car continues moving along
the track. You want to know how the launch speed of the car depends on the parameters
of the system that you can adjust. You decide to calculate how the launch velocity of the
car depends on the mass of the car, the mass of the hanging mass and the distance the
hanging mass falls.
In terms of the underlined quantities above, what is the velocity of the
car after being pulled by a given mass for a known distance?
Equipment:
A cart is pulled along a level track by a string that passes over a pulley and is attached to
a mass that hangs down. The set-up is exactly the same as the one we have used in
previous activities. You will be able to vary the mass of hanging mass, the mass of cart
(above a minimum mass of 1 kg), and the length of the string. The mass will fall
through a distance that is much less than the length of the track. That is, the mass hits
the floor significantly before the cart hits the end of the track. You will also have a
motion detector and LoggerPro software to use in making measurements.
Homework/Preparation Questions:
All of the following questions should already be written out on paper. This paper is the
beginning of your activity write-up.
1. Make a sketch of the problem situation (equipment). Draw vectors which show
the direction and relative magnitude of the motion of the objects (both velocity
and acceleration) at the two interesting times in the problem: when the car stars
from rest and just before the block hits the floor. Draw vector to show all of the
forces on the hanging mass, the cart and the string. Assign appropriate symbols to
all of the quantities that describe the motion and the forces. If two quantities have
the same magnitude, use the same symbol but write down your justification for
doing so. For example, the car and the hanging mass have the same magnitude of
velocity. Explain why. Decide on your origin and coordinate system and draw it.
2. The known quantities in this problem are the mass of the hanging mass, the mass
of the car and the height of the hanging mass above the floor. Assign these
quantities symbols so that you can use them in algebra. The unknown quantity is
the velocity of the car and the hanging mass just before the block hits the floor.
There are other unknowns as well. List them. What is the relation between what
you really want to know (the velocity of the car after the block hits the floor) and
what you can calculate (the velocity of the car just before the block hits the
floor)?
3. Write down what principles of Physics you will use to solve this problem.
Because forces determine the motion of the car, using Newton’s 2nd Law to relate
the sum of the forces on each object and its motion is a good bet. We will do this
in class. For now, assume that you can find an algebraic expression for the
acceleration of the cart. Write down any kinematics equations that are
appropriate to this situation. You will have to decide if the acceleration each
object is constant or varies during the time interval for which your calculation is
valid. What is the time interval? Starting with the two basic equations of motion
with constant acceleration we have used in class so far, derive an expression for
the acceleration of the cart just after the hanging mass hits the ground in terms of
only the acceleration of the cart, the mass of the cart, the hanging mass, the
acceleration due to gravity and the distance that the hanging mass falls. Note that
you must have an expression that does not contain the time period.
In Class Work
The first thing that you should do is to compare everyone in your group’s expressions for
the launch (final) velocity of the cart in terms of the mass of the cart, the distance the
hanging mass falls, the acceleration of the cart and the mass of the hanging mass. The
expression should not contain the time variable. Do all of you agree on the expression?
If not, come to some consensus on what is correct.
1. Freebody Diagrams and Force Equations: Draw separate free-body diagrams
for the cart and hanging mass after they start accelerating. Check to see if any of
these forces are related by Newton’s 3rd law (Third law pairs). An example of a
third law pair is as follows: If you push the cart, there is a force from your hand
on the cart. There is also a force from the cart on your hand. These two forces
are a Newton’s third law pair. Newton’s third law pairs are forces between the
same two objects, but which object is exerting the force and which is being acted
on are exchanged. If there are any, list all Newton’s 3rd law pairs in this problem.
For easy reference, it is useful to draw the acceleration vector for the object next
to its free-body diagram. The origin (tail) of all vectors for one object should be at
the same place. For each object, write down Newton’s 2nd law along each of the
axis of the coordinate system ( x and y) . It is important to make sure that all of
your signs are correct. For example, if the acceleration of the car is in the +
direction, is the acceleration of the hanging mass + or -? Your answer will
depend on how you define your coordinate system.
2. Solving for acceleration: Use the relationships that you come up with in the step
above to solve for the acceleration of the cart during the time that the hanging
mass is falling. The acceleration expression should contain only the mass of the
cart, the hang mass and the acceleration due to gravity. You must eliminate all
other variables from the expression, because we cannot measure (and do not know
the value of) these other variables.
3. Solving for the velocity of the cart after the block hits the floor: Combine the
expression for acceleration that you derived above and the expression for the
velocity of the cart that you derived as part of your homework. The result should
be an expression for velocity of the cart after the hang mass hits the floor that is a
function of ONLY: the mass of the cart, the hanging mass, the distance the
hanging mass falls and the acceleration due to gravity.
4. Exploration: Adjust the starting point of the cart so that you start at least a half of
a meter away from the motion detector. You will be measuring the velocity of the
cart after the hanging mass hits the floor but before the cart hits the end of the
track. Is the velocity of the cart constant during this time period? Why or Why
Not? Choose a mass for the hanging mass that allows the cart to achieve a reliably
measurable velocity before the hanging mass hits the floor. Please don’t let the
cart smash into the end stop on the track too hard. Record the mass of the cart
(0.5 kg), the mass of the hanging mass you will use, and the distance through
which the mass will fall. There is a “meter stick” on the low friction tracks that
you are using. Use your expression for velocity of the cart to determine what you
think the resulting velocity of the cart should be with the set-up you are using.
Record that value here and show all of your work in determination of it. Draw a
sketch of what you predict the velocity versus time and acceleration versus time
graphs will look like.
5. Making Experimental Measurements: Get the file pos,vel,acc.MBL from the
webpage if you do not yet have it on your computer. Use LoggerPro to measure
the velocity of the cart after the hanging mass hits the ground. Record that value.
Repeat the measurement at least once and record the second value. Be as accurate
as you can in determining the velocity from the LoggerPro graphs.
6. Comparing your predicted value with the measured values. Do the two
values agree? If not, why not. What are the limitation on the accuracy of your
measurements and analysis?