Download Ratio of Charge to Mass (e/m) for the Electron

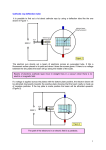
Ph 122
quark%/~bland/docs/manuals/ph122/eoverm/eoverm.doc
June 26, 2017
Ratio of Charge to Mass (e/m) for the Electron
In this experiment we observe the motion of free electrons in a vacuum tube.
From their response to electric and magnetic fields the ratio of charge to mass for
the electron can be determined.
At the turn of the century several crucial experiments were performed to demonstrate the
atomic structure of matter. In 1897 J.J. Thompson was able to observe the motion of single
electrons in electric and magnetic fields, and so determine the ratio of the electron’s charge, e, to
its mass, m. This demonstrated some interesting things about the atom. First of all, this ratio is
exactly the same for all electrons, suggesting that they are fundamental particles rather than just
fragments of matter. Secondly, since the typical charge on atomic particles was known
approximately at the time, the mass of the electron could be estimated, and it turns out to be very
tiny compared to the mass of an atom. This was the first suggestion that the electron in an atom
might be a small particle orbiting a larger one, like the Earth in the solar system.
I. Theory
A. The apparatus. This experiment is carried out in a special vacuum tube which contains a
small amount of mercury vapor. Electrons emitted by a heated cathode are accelerated by the
voltage applied between the cathode and anode. Some of the electrons come out in a narrow
beam through a circular hole in the center of the cylinder. This emission is then focused into a
narrow beam by the grid of the tube. When electrons of sufficiently high kinetic energy leaving
the cathode collide with mercury atoms a fraction of the atoms become ionized. Upon
recombination of the ions with stray electrons, a characteristic blue color is observed. This
makes the path of the beam of electrons visible as the electrons travel through the mercury
vapor.
A magnetic field is applied using a pair of coils of wire. Two coils, separated by a distance
equal to their radius, are referred to as Helmholz coils. The advantage of this configuration is
that it gives a rather uniform field over a rather large area around the centerpoint.
The magnetic field at the center of the tube is calculated from a relation given in its manual,
B = 7.7 x 10-4 I
where I is the current in amps, and B is in Teslas.
e/m - 1
B. Electrons in a magnetic field. A charged particle moving in a magnetic field experiences
a force which is to the side (perpendicular to the
particle’s motion) and perpendicular to the magnetic
B (out of
field. If the particle’s initial velocity is perpendicular to a
paper)
uniform magnetic field, it will move in a circle. This
situation is shown in figure 1.
The magnetic force, equal to evB, is the only force on
the electron; so, Newton’s second law (F=ma) gives
evB 
mv 2
r
F
The direction of the force on the electron is given by the
right-hand rule. Walker gives this rule as follows: "To
find the direction of the magnetic force on a positive
v
charge, start by pointing the fingers of your right hand in
the direction of the velocity, v. Now, curl your fingers
Figure 1. Force on an electron in a
toward the direction of B. Your thumb points in the
uniform magnetic field.
direction of F. If the charge is negative, the force points
opposite to the direction or your thumb." You should be able to use this rule to confirm that the
force on the electron shown in figure 1 is towards the center of the circle.
The velocity v of the electron can be related to the accelerating voltage, using energy
conservation:
Drop in potential energy  gain in kinetic energy
eV 
1 2
mv
2
Solving this expression for v, and substituting into eB = mv/r, gives us the relationship:
e
2V
 2 2 (1)
m Br
II. Experimental Procedure
Turn the apparatus on, and wait for warm-up (about one minute). Turn the voltage up to about
200 volts. A beam will now be observed on the glass envelope opposite the anode. Adjust the
current through the coils and observe how the beam curves up into the sphere of the tube and
eventually bends over to complete a full circle.
Measuring the sign of the electron’s charge:
First method: Using a compass, determine the direction of the magnetic field applied by the
coils. Then, from the direction the electrons bend, determine whether their charge is positive or
negative. Explain your reasoning.
e/m - 2
Second method: Turn off the current to the coils. Use a permanent magnet with known north
and south poles to apply a known magnetic field to the electron beam. From the direction of
deflection of the electrons, determine whether their sign is positive or negative. Explain your
reasoning.
Now turn the magnetic field back on, and bring one end of a bar magnet as close as you can to
the electrons' path and observe the spiral path which the electrons now follow. Can you explain
why the presence of the extra field distorts the electron's path? How will the Earth's field affect
the motion of the electrons? Predict the direction of the bar magnet so as to reduce the radius of
the electron's orbit; then try it.
r as a function of voltage. Here we plan to measure the radius r of the electron’s circular path
as a function of the accelerating voltage V. Note that equation (1) can be solved for V, giving
V = B2e/(2m) r2
or
y=ax,
where y = V, x = r2, and the slope a of the line is given by
a = B2e/(2m).
Thus if we plot V as a function of r2, the curve should be a straight line, whose slope is related to
e/m. Solving for e/m gives
e/m = 2a /B2.
Set I at 1.5 A. This determines the value of the magnetic field produced by the coils; the
relationship, from the equipment manual, is
B = k I, where k = 7.7 x 10-4 T/A .
Calculate the value of B corresponding to the current you have set.
Then vary the accelerating voltage V and measure r, the radius of the orbit, as a function of V,
over the widest range of voltages for which a measurement is feasible. The most convenient way
to analyze this data is to open an EXCEL spreadsheet, though plotting by hand is also quite
acceptable. See the first experiment, "Data Analysis on the IBM PC," for instructions on plotting
and linear fits. Plot V versus r2 and find the slope of the graph (linest is the easiest). Then use
your value of the slope to determine e/m, using the relation given above. Note: to get the slope
in the right units, r should be expressed in meters.
r as a function of current. Here we plan to measure the radius r of the electron’s circular path
as a function of the accelerating voltage I, at constant V. Note that if we substitute B = kI into
equation (1), it can be solved for I, giving
I = (2Vm/(k2e))1/2 (1/r)
Thus if we plot I as a function of 1/r, the curve should be a straight line, whose slope is related to
e/m. In this case the slope a is given by
a = (2Vm/(k2e))1/2,
and the charge-to-mass ratio is calculated from it using the relation
e/m - 3
e/m = 2V/(k2a2).
Now set V to a fixed value (200 V). Then determine r for various settings of I, the current
through the coils. Plot I against 1/r and find the slope of the graph. Then use your value of the
slope to determine e/m, using the relation given above. Note: to get the slope in the right units,
r should be expressed in meters.
Now you have two experimentally determined values for e/m. Use them to calculate a best
value (the average) and the error on the average value. [See the first experiment, "Data Analysis
on the IBM PC," for instructions on calculating averages and standard deviations.] State your
final result, complete with error.
What systematic errors might have been ignored in assigning the error?
Calculate the accepted value for e/m. (e = 1.6 x 10-19 C, m = 9.1 x 10-31 kg.) Compare it with
your measurement in the standard way (discrepancy, number of sigmas of discrepancy, quality of
agreement). Is your result credible? What systematic errors might have been ignored in
assigning the error? (What about the Earth's magnetic field?)
III. Equipment
Daedalon e/m apparatus
bar magnet
compass
e/m - 4