* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Conservation of Linear Momentum
Four-vector wikipedia , lookup
Atomic theory wikipedia , lookup
Routhian mechanics wikipedia , lookup
Symmetry in quantum mechanics wikipedia , lookup
Centripetal force wikipedia , lookup
Uncertainty principle wikipedia , lookup
Tensor operator wikipedia , lookup
Derivations of the Lorentz transformations wikipedia , lookup
Classical mechanics wikipedia , lookup
Specific impulse wikipedia , lookup
Quantum vacuum thruster wikipedia , lookup
Relativistic quantum mechanics wikipedia , lookup
Bra–ket notation wikipedia , lookup
Laplace–Runge–Lenz vector wikipedia , lookup
Accretion disk wikipedia , lookup
Electromagnetic mass wikipedia , lookup
Seismometer wikipedia , lookup
Equations of motion wikipedia , lookup
Classical central-force problem wikipedia , lookup
Angular momentum wikipedia , lookup
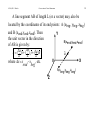
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Angular momentum operator wikipedia , lookup
Center of mass wikipedia , lookup
Photon polarization wikipedia , lookup
Rigid body dynamics wikipedia , lookup
Relativistic mechanics wikipedia , lookup
Newton's laws of motion wikipedia , lookup
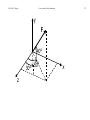
2000, W. E. Haisler Conservation of Linear Momentum ENGR 211 Principles of Engineering I (Conservation Principles in Engineering Mechanics) Conservation of Linear Momentum Introduction Conservation of Linear Momentum Equations Linear Momentum and Newton's Laws of Motion Steady State Other Special Cases Reference Frame 1 2000, W. E. Haisler 2 Conservation of Linear Momentum Introduction The linear momentum of a system is defined to be the product of the mass (m) and velocity ( v ) of the system. Since velocity is a vector, then linear momentum is a vector quantity (has three components). Because linear momentum is a conserved property, there is no generation or consumption. Therefore, the conservation statement becomes LM entering LM leaving system during - system during time period time period Accumulation of LM within system during time period Accumulation of LM LM in system LM in system at end of within system - at beginning of during dime period time period time period 2000, W. E. Haisler Conservation of Linear Momentum Linear Momentum Possessed by Mass Linear Momentum may enter or leave the system with mass. Linear Momentum may also enter or leave the system at a certain rate. When mass enters a system traveling at a velocity ( v ), it adds momentum to the system. The rate at which mass (m) enters the system is m (where in dm m in ) and therefore the rate at which linear momentum in dt enters the system is given by (m v ) . Similarly, rate at which in the linear momentum leaves the system is (m v )out . 3 2000, W. E. Haisler Conservation of Linear Momentum The proper way to look a momentum rate is as follows momentum momentum mass time mass time If p linear momentum mv , then the above can be written in (mv ) d p m m v m equation form: dt If there are multiple masses entering or leaving the system (say n of them), then we simply add them up: n mv i in i1 and n mv i out i1 Note that the velocity v of a mass can be thought of as it's linear momentum per mass. 4 2000, W. E. Haisler Conservation of Linear Momentum 5 Linear Momentum in Transit: Forces Why do we refer to "Forces" as "Linear Momentum in Transit?" Newton's 2nd Laws states that the external forces on a system are connected to the time rate of change of linear momentum within the system! f ext dp d (mv ) dt dt Linear momentum enters the system as the result of forces that act upon the mass in the system. By Newton's second law, an external force f ext acting on a system provides momentum to the system at rate fext . These forces may act as surface or contact forces on the system boundary (called tractions), or they may act as body forces on the entire mass of the system (for example, body forces due to gravity). 2000, W. E. Haisler 6 Conservation of Linear Momentum Schematic for Conservation of Linear Momentum Resultant External Forces Acting on System Surroundings Linear Momentum Entering System System Linear Momentum Surroundings Linear Momentum Leaving System System Boundary 2000, W. E. Haisler Conservation of Linear Momentum The external forces may be due to: pressure acting over the surface area of the system drag or frictional forces acting on the surface supporting structure which holds the system in place (cause forces acting on the surface) gravitational and electrostatic body forces acting on the system volume 7 2000, W. E. Haisler Conservation of Linear Momentum Conservation of Linear Momentum Equations We can now state the rate equation for conservation of linear momentum as: dpsys (m v ) (m v ) f out ext dt in The momentum of the system may change with time because of mass that enters and leaves, and because of external forces that act on the system. As mass enters the system, the amount of linear momentum that enters the system is this [mass flow rate] times the [momentum per unit mass (i.e., the velocity) of the mass]. 8 2000, W. E. Haisler Conservation of Linear Momentum 9 We must keep in mind that conservation of linear momentum is a vector equation! Consequently, we can write in component form. For a Cartesian coordinate system, we have x-direction: d ( px)sys (m v x ) (m v x ) ( f x ) out ext dt in y-direction: d ( p y)sys (m v y ) (m v y ) ( f y ) out ext dt in z-direction: d ( pz )sys (m v z ) (m v z ) ( f z ) out ext dt in 2000, W. E. Haisler Conservation of Linear Momentum Linear Momentum of the System The linear momentum of the system may be written (for n particles in the system) as n psys (mv ) i i 1 sys 10 2000, W. E. Haisler Conservation of Linear Momentum Rate of Change of Linear Momentum of the System Consider the time rate of change of linear momentum of the system (left side of conservation equation) and use the product rule for the derivative: dpsys d (mv )sys dmsys dvsys vsys msys dt dt dt dt If the mass of the system is constant with time, then the time rate of change of linear momentum reduces to dpsys dvsys msys dt dt Note that the time derivative of the velocity becomes the dvsys asys acceleration: dt 11 2000, W. E. Haisler Conservation of Linear Momentum 12 Velocity of the Center of Mass For rigid bodies and other closed systems, it is convenient to define a velocity that characterizes the system as a whole. This velocity is an average velocity for the system and acts at the center of mass. We define the velocity of the center of mass, v , such that the system mass times the velocity of the mass G center is equal to system linear momentum: n msysv (mv )i G i1 sys and solving for the velocity of the center of mass: 2000, W. E. Haisler Conservation of Linear Momentum n (mv )i sys v i 1 m G sys If the size of the elements mi becomes differentially small, the summation process becomes an integration and the velocity of the center of mass becomes v sys G m sys v dm This is sometimes called the mass-average velocity of the system. 13 2000, W. E. Haisler Conservation of Linear Momentum 14 Recall that the velocity of an element of mass is defined to be the time rate of change of the position vector describing it's location. For a particle with velocity vG whose position is refined by the position vector rG : _ vG y _ rG x z dr v G G dt r xi yj zk , x=x(t), etc. G dy d dx dz vG G (xi yj zk ) i j k vxi vy j vzk dt dt dt dt dt dr The center of mass can be determined in terms of the position vectors of all of the mass elements of the system: 2000, W. E. Haisler 15 Conservation of Linear Momentum y _ rG x n (mr )i i 1 sys r m G sys z As the size of mass particle becomes differentially small, we can replace the summation by an integration to obtain r sys G m sys r dm This definition of the center of mass applies only for a closed system (one in which there is no mass into or out of the system). 2000, W. E. Haisler Conservation of Linear Momentum When the system is closed (no mass in or out of system), the conservation of linear momentum becomes dv dpsys d (msys v ) G m ( G )m a f ext dt sys dt sys G dt 16 2000, W. E. Haisler 17 Conservation of Linear Momentum Integral (Finite Time Period) Equation The rate form of the conservation of linear momentum equation can be integrated over a finite time period to obtain dp t sys end dt t dt beg t end (m v) dt in t beg t end (m v) dt out t beg t end f dt ext t beg The above equation can also be written for a finite time period as ( psys) ( psys) (m v ) t (m v ) t ( f )t out ext end beg in or ( psys) ( psys) (mv ) (mv ) ( f )t out ext end beg in 2000, W. E. Haisler Conservation of Linear Momentum 18 Linear Momentum and Newton's Laws of Motion The concept of conservation of linear momentum applied to a rigid body, together with the realization that forces exchange momentum between the surroundings and the body, is actually a statement of Newton's three laws of motion. Newton's first law of motion - A body which is at rest will stay at rest unless acted upon by an external force. In other words, a body does not spontaneously generate momentum; momentum is conserved. 2000, W. E. Haisler Conservation of Linear Momentum 19 Newton's second law of motion - For a body (system) of constant mass, the sum of the external forces is equal to the mass times acceleration of the body. This is clearly a result of the conservation of linear momentum when m m out 0 so in dm sys that by conservation of mass 0 dt Newton's third law of motion - For every force there is an opposite and equal reaction force. This also implies conservation of linear momentum. A force acting on a system by the surroundings (boundary forces or body forces) provides an opposite and equal force exerted on the surroundings. Thus, momentum transferred to the system must have been provided or given up by the surroundings, implying conservation of linear momentum. 2000, W. E. Haisler Conservation of Linear Momentum Steady State The steady state condition for a system means that the system is not changing with time and hence the accumulation within the system is zero for any time period. ( psys) ( psys) 0 end beg dpsys 0 or, for any instant of time: dt For a finite time period: Through conservation of linear momentum, steady state implies: 0 (m v ) (m v )out f in ext dmsys Steady state also implies that the term 0 in the dt conservation of mass law. 20 2000, W. E. Haisler Conservation of Linear Momentum For rigid body statics (no mass enters or leaves the system and the body is at steady state), linear momentum reduces to 0 f ext 21 2000, W. E. Haisler 22 Conservation of Linear Momentum Reference Frame In order to define velocity and liner momentum, we must define a reference coordinate system. Position and velocity are then measured with respect to the origin of the coordinate system. For this purpose, we can choose any reference frame so long as it is an inertial reference frame, i.e., one that is not accelerating (has constant velocity and not rotating). v Consider a block sliding along a plane at a velocity of vref with an y attached pendulum as shown to the x right. The x-y frame is fixed. The x'-y' frame is attached to the block fixed so that it also has a velocity of vref. v (x, y) v v (x', y') ref y’ ref x’ 2000, W. E. Haisler 23 Conservation of Linear Momentum Now lets write COLM with respect to the stationary x-y reference frame (vxy v in x - y coordinate system) d[mvxy]sys (m v xy ) f ext dt in / out (x,y coords.) (1) Substitute the relation between the two coordinates systems into (1): d[m(v v )]sys ref x' y' [m (v v )] f ext dt ref x' y' in / out Taking the time derivative on the left side and rearranging, the above can be written: 2000, W. E. Haisler 24 Conservation of Linear Momentum dv d (mv )sys dm sys v x' y' msys ref v m dt dt ref dt ref in / out (m v ) x' y' in / out f ext The first underlined term is zero since v is constant. The ref dmsys m 0 since this is double underlined term in / out dt conservation of mass (for no mass gen/con). Thus, the COLM equation in the x'-y' frame reduces to d[mv ]sys x' y' (m v ) f ext dt x' y' in / out (x',y' coords.) (2) 2000, W. E. Haisler Conservation of Linear Momentum Note that equation (2) is identical to equation (1) except for the change in reference frame. Since (2) was derived from (1), we see that COLM is independent of coordinate system as long as we use an inertial reference frame for the velocities and the external forces f ext are independent of the reference frame. 25 2000, W. E. Haisler 26 Conservation of Linear Momentum Some notes on unit and radius vectors. Consider a line element OP of length L (or a vector L ) where L (x2 y2 z2)1/ 2. The vector L is given by L xi yj zk . Note: "O" is at the origin. Y P(x,y,z) y L x 0 Z z y X z x We define the following angles: x angle between x -axis and vector L y angle between y -axis and vector L z angle between z -axis and vector L 2000, W. E. Haisler Conservation of Linear Momentum 27 Now the cosine of each angle is: cos x x , cos y y , and L L cos z z . Note that x is an angle in the plane containing the L x-axis and the line segment OP. A unit vector u in the direction of L is given by u ( x )i ( y ) j ( z )k (cos x)i (cos y ) j (cos z )k L L L where L L (x2 y2 z2)1/ 2 . The cosines of the three angles are often referred to as the direction cosines of the line OP. From geometry and trigonometry, one can prove that cos2 x cos2 y cos2 z 1. Thus you only need to specify two of the angles – the third must satisfy the trig relation. This is similar to a unit vector – two of the components (say x and y) can be specified, but the third (say z) must satisfy x2 y2 z2 1!! 2000, W. E. Haisler 28 Conservation of Linear Momentum A line segment AB of length L (or a vector) may also be located by the coordinates of its end points: A (xbeg, ybeg, zbeg) and B (xend,yend,zend). Then the unit vector in the direction of AB is given by: u (x)i (y ) j (z )k L L L where x x x , etc. end beg Y B(xend,yend,zend ) _ u X 0 ) ,z ,y A(x beg beg beg Z 2000, W. E. Haisler 29 Conservation of Linear Momentum y F 40o o 30o 50 z x 2000, W. E. Haisler Conservation of Linear Momentum Example: Vectors P and P in x-y plane: 1 2 Y _ P 2 _ P 1 40o 0 Z 30o X u cos(30)i cos(60) j cos(90)k 1 P P u 1 1 1 u cos(140)i cos(50) j cos(90)k 2 P P u 2 2 2 30 2000, W. E. Haisler 31 Conservation of Linear Momentum lbm ft Note on conversion of lb f and in American Engineering sec 2 units. lbm ft 1 lb f 32.174 sec 2 lbm ft gc 32.174 lb sec 2 f lbm ft 2 F m(lb ) g (ft/sec ) m 2 sec 2) g ( ft/sec F (lb f ) m(lbm) g c lb f Note units: gg c lbm 2000, W. E. Haisler Conservation of Linear Momentum 32 Notes on determining the mass entering a system. The mass entering a system boundary (through an area) during a period of time may be determined or specified in many ways. 1. We can simple state that a certain amount of mass enters the system during a specified time period, i.e., m mass . in time 2. However, a more common situation is when one specifies that a fluid (of given density) flows through an area at a specified velocity normal to the area. In this case, consider the following dimensional analysis: m mass densityvolume m L31s m L2 Ls density area velocity in time time L3 L3 So the rate of mass entering a system for a mass with density and passing through an area A with a velocity Vn normal to the area is given by: m AVn . in 2000, W. E. Haisler Conservation of Linear Momentum 3. Another common way to describe mass flow is by the mass flux rate, or the mass per unit area per unit time. mass flux rate mass densityvolume densitylength densityvelocity . areatime areatime time To obtain the mass entering a system (in terms of mass flux rate) we write: mass entering mass flux rate area time ( mass )(area)(time period ) mass areatime m mass flux rate areatime period in 33