Download Planetary Fact Sheet – Metric

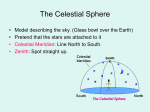
Astronomy Assignment #2
Text Problems:
Unit Number
5
6
7
Questions for Review
1, 2, 4, 5, 6
1, 4, 6, 7
1, 2, 3, 6
Problems
10, 11, 13, 14
15, 16
(10, 12, 14 not included in these solutions – sorry)
Unit 5
10. What are your latitude and longitude? What are the latitude and longitude at the point on the
Earth exactly opposite you? What geographic features are located there?
A Google search of “latitude and longitude of Syracuse, NY” yields our latitude is about 43
degrees N and longitude is about 76 degrees W.
Just opposite us on the globe implies that we (1) take the same latitude but opposite hemisphere
and (2) add 180 degrees to the longitude (and then play with the number so that it is between
zero and 180 degrees either E or W. So…the point opposite Syracuse, NY on the Earth has a
latitude of 43 degrees S and the longitude is (76 W + 180 = 256 W = ) 104 degrees E longitude.
On the map below the position of Syracuse, NY and its opposite point are marked with Xs. You
can see that our opposite point is in the middle of the ocean off the southwest corner of Australia.
X
X
11. Your observatory lies at a latitude of 45N and a longitude of 90W. You wish to observe
three celestial objects that have declinations of +87, -40, and -67. Which of these objects can
you observe?
This question requires a fairly complete understanding of the celestial coordinate system and the
celestial sphere model. According to the last sentence on page 43 “if a star’s declination
matches your latitude it will pass over through zenith”. This means that the declination of your
zenith is just your latitude. Observing from 45N will mean that 45 declination will be directly
over your head. Following Figure 5.4A on page 42, you can see that the horizon is 90 from the
zenith. Thus, any star that is within 90s from the declination of your zenith will be visible. As
seen from 45N, all stars between +90 declination and -45 declination will eventually be
visible over the horizon. So, you will be able to see the objects at +87 and -40 declination ,
but not the object at -67 declination..
13. Boston and Rome are at the same latitude, but Boston is at a longitude of 71W, while Rome
is at 12E. If M31 passes through the zenith at a particular time in Rome, how many hours later
will it pass through the zenith in Boston?
This question requires knowledge of the relationship between the celestial coordinate system and
the rotation of the Earth. As stated on page 43, “Each hour of RA equals 15;…if a star at RA
=2h is overhead now, a star at RA =5h will be overhead three hours from now.” Thus, if were to
calculate the number of degrees longitude between Boston and Rome, then divide that difference
by 15 per hour, we would have the time in hours between M31 passing over both cities.
Number of degrees longitude between Boston and Rome is 83. This divided by 15 per hour
gives a time difference between M31 over Rome than Boston as 5.53 hours or 5 hours and 32
minutes.
14. How far is the celestial equator from your zenith if your latitude is 42N? 34S?
This question requires a fairly complete understanding of the celestial coordinate system and the
celestial sphere model. According to the last sentence on page 43 “if a star’s declination
matches your latitude it will pass over through zenith”. This means that the declination of your
zenith is just your latitude. Observing from 42N will mean that 42 declination will be directly
over your head. Since 42 declination is 42 away from the celestial equator, the celestial
equator must be 42 away from your zenith at this location. Observing from 34S latitude, will
mean that the celestial equator is 34 away from your zenith at that location.
Draw a celestial sphere, as shown in Figure 5.3, as it would appear if you were standing at the
North Pole. What celestial object lies directly above you? What celestial object lies on the
horizon? Now draw a celestial sphere, as shown in Figure 5.3, as it would appear if you were
standing at the equator. What celestial object lies directly above you? What celestial object lies
on the horizon?
The following figures were obtained from Nick Strobel's Astronomy Notes. Go to his site at
www.astronomynotes.com for the updated and corrected version. (Dr. Jaquin’s personal note:
Nick Strobel does a fine job describing the celestial sphere and the apparent motion of the stars.
Check out his astronomy lecture notes. )
If you joined Santa last Christmas at the north pole (90 degrees latitude), you would have seen
Polaris straight overhead and the celestial equator on your horizon. The point straight overhead
on the celestial sphere for any observer is called the zenith and is always 90 degrees from the
horizon. The arc that goes through the north point on the horizon, zenith, and south point on the
horizon is called the meridian. The positions of the zenith and meridian with respect to the stars
will change as the celestial sphere rotates and if the observer changes locations on the Earth, but
those reference marks do not change with respect to the observer's horizon. Any celestial object
crossing the meridian is at its highest altitude (distance from the horizon) during that night (or
day). The angle the star paths make with respect to the horizon = 90 degrees - (observer's
latitude).
.
To warm Rudolph's frozen nose, Santa heads down to the equator (0 degrees latitude). At the
equator, you see the celestial equator arcing from exactly east to the zenith to exactly west. The
NCP is on your northern horizon. At the equator you see one-half of every star's total 24-hour
path around you so all stars are up for 12 hours. All of the stars rise and set perpendicular to the
horizon (at an angle = 90 - 0 = 90 degrees).
Here is a summary of the positions of the celestial reference marks (note that ``altitude'' means the
number of degrees above the horizon):

Meridian always goes through due North, zenith, and due South points.







Altitude of zenith = 90° (straight overhead) always.
Altitude of celestial pole = observer's latitude. Observers in northern hemisphere see NCP;
observers in southern hemisphere see SCP.
Altitude of celestial equator on meridian = 90 - observer's latitude.
Celestial equator always intercepts horizon at exactly East and exactly West points.
Angle celestial equator (and any star path) makes with horizon = 90 - observer's latitude.
Stars move parallel to the celestial equator.
Circumpolar object's distance from celestial pole = observer's latitude.
Select this link to show an animation of the celestial sphere changing with latitude.
(You'll want your web browser to fill most of your screen!)
Check out the Rotating Sky module from the University of Nebraska-Lincoln's Astronomy
Education program to explore the connection between your position on the Earth and the path of
the stars (link will appear in a new window---choose the "Rotating Sky" part).
Unit 6
1. If the shape of the Earth’s orbit was unaltered but its rotation axis was shifted so that it had no
tilt with respect to the orbit, how would the seasons be affected?
This requires you understand the relationship between the tilt of the Earth and its seasons. This
is summarized in unit 6.3 on pages 47 & 48. If the shape of the Earth’s orbit was unaltered but its
rotation axis was shifted so that it had no tilt with respect to the orbit, then each hemisphere of the Earth
would receive the same amount of sunlight all year long. There would be no variation in the amount of
sunlight or the length of day at any latitude. Thus seasons would not exist. There would be not summer
or winter, anywhere, anytime. As you can see form the table below, those planets that have a very small
tilt and, therefore, no seasons, include Mercury, Venus, the Moon and Jupiter.
Planetary Fact Sheet – Metric
http://nssdc.gsfc.nasa.gov/planetary/factsheet/
Axial
Tilt
MERCURY
VENUS
EARTH
MOON
MARS
JUPITER
SATURN
URANUS
NEPTUNE
PLUTO
0.01
-2.6
23.5
6.7
25.2
3.1
26.7
-87.8
28.3
-57.5
(degrees)
15. Describe the motion you would see on the solstices and the equinoxes if you were observing the
Sun from the Artic Circle at latitude of 66.5N.
This question requires you to understand the apparent motion of the Sun during the year it terms
of its declination and the celestial sphere. Recall that the declination of your zenith is equal to
your latitude. So observing from the Artic Circle at latitude of 66.5N, your zenith would be at
66.5 degrees declination. Looking south, you would be able to see stars down to (66.5- 90)
= -23.5 declination.
On the summer solstice, when the Sun has a declination of +23.5, the Sun would be only
(66.5- 23.5) = 42 from the zenith and would be up all day. The “all day” part follows form
knowing that the NCP will be 66.5 above the northern horizon at this location and all objects
between the NCP and (90- 66.5) = 24.5 in declination will be circumpolar.
On the equinoxes, when the Sun has a declination of 0, the Sun would be only (66.5- 0) =
66.5 from the zenith visible during the day. However, since the circumpolar region extends to
only 24.5 in declination, the Sun will rise and set after 12 hours of daylight.
. On the winter solstice, when the Sun has a declination of -23.5, the Sun would be only (66.5-23.5) = 90 from the zenith and would lie exactly on the horizon at noon. The Sun would
never rise that day.
16. If you wish to observe a star with a right ascension of 12h, what would be the best time of year
to observe it? What would be the best time to observe a star with a right ascension of 6h?
The answer to this type of question is best understood by using the Whole Sky Map that we drew
in class. See below.
Declination
Night
Day
Night
+23 ½ 

0
-23 ½ 
12h
6h
0h
18h
12h
Right Ascension
The star is best seen at night. That requires that the Sun be far away from the star on the celestial
sphere, since the area around the Sun will be daylight. For simplicity, lets that the sky is light 6 hours
either side of the Sun. So, the best time to observe the star will be when the Sun is as far away as
possible on the celestial sphere,or equivalently, 12 hours away. If the star has RA = 12h, then the Sun
should be at RA=0h for best viewing of the star. The diagram illustrates the concept by shading the area
beyond ±6 hours around the Sun as night. The Sun is at 0h RA on Mar 22 (Spring Equinox). So the best
time to view this star is on March 22.
For a star at 6h RA, the Sun should be a 12 hours of RA away or at RA = 18h. This corresponds to the
Sun being at the Winter Solstice on December 22. The diagram below illustrates the situation. The best
time to view this star is in late December.
Declination
Night
+23 ½ 
Day
0

-23 ½ 
12h
6h
0h
Right Ascension
18h
12h