* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Dynamics
Magnetic monopole wikipedia , lookup
Multiferroics wikipedia , lookup
Eddy current wikipedia , lookup
Electricity wikipedia , lookup
History of electromagnetic theory wikipedia , lookup
Electrostatics wikipedia , lookup
Faraday paradox wikipedia , lookup
Maxwell's equations wikipedia , lookup
Computational electromagnetics wikipedia , lookup
Welcome to Physics 321 My Name is Brett Fadem What is Electrodynamics and How Does it Fit Into The General Scheme of Physics? First, what is the distinction between kinematics and dynamics? The Distinction between Kinematics and Dynamics. Kinematics Kinematics is the study of motion without regard to the cause. Kinesis is the Greek word for motion. Dynamics Dynamics is the study of the causes of motion. Dunamis is the Greek word for power. We call the Causes of motion, “forces.” Source: The Dr. Physics Homepage. Please include attributions in your work. So, “electrodynamics” is the study of the electric and magnetic causes of motion (or, electric and magnetic forces). But what part of physics studies the resulting motion of objects When acted upon by a force? Mechanics! Describe the force and mechanics will tell you how things move. What do you remember from classical mechanics? 1st Law 2nd Law 3rd Law Newton’s Laws Objects in motion, remain in motion. Objects at rest remain at rest. 2 dp d r F ma m 2 dt dt F12 F21 1 Relativistic Corrections? 2 Special Relativity Galilean Transformations Lorentz Transformations x x vt y y x ( x vt) z z t t p mv 1 2 KE mv 2 y y z z t (t vx p mv KE ( 1)mc2 c 2 ) 1 1 (v c ) 2 Classical Mechanics (Newton: 1642-1727) Special Relativity (Einstein. 1905 was a big year.) Quantum Mechanics (Bohr, Heisenberg, Schrodinger, et al.) Quantum Field Theory (Dirac, Pauli, Feynman, Schwinger, et al.) The Four Forces to Which Mechanics is Applied: 1. Strong 2. Electromagnetic: complete theory in all 4 realms! 3. Weak 4. Gravitational So, electrodynamics is the study of the electromagnetic force, and mechanics tells us how a system will behave when subjected to that force. Unification? Electricity Magnetism Electromagnetism “QED” Electroweak Weak Force Strong Force? Gravity ?? Quantum Chromodynamics “QCD” General Relativity “In this Course, we are going to focus on classical electromagnetism, that is, electromagnetism in the context of classical physics.” Comparison of Strength of Electromagnetic vs. Gravitational Force FEM 1 q1q2 40 r 2 m1m2 FG G 2 r mp=1.67x10-27 Kg e =1.6x10-19 C εo=8.85x10-12 C2/(Nm2) G=6.67x10-11 (Nm2)/Kg2 1 1 FEM FG 2 (1.6 1019 C ) 2 2 e 1 2 C 12 e 4 (8.85 10 ) 2 2 4o r 4o Nm 2 2 2 mp Gmp 11 Nm 27 2 ( 6 . 67 10 )( 1 . 67 10 Kg ) G 2 Kg 2 r FEM 1.2 1036 Electromagnetism is much stronger! FG Maxwell’s Equations Qenc E da E B d a 0 B 0 S o S d E dl dt o B E t Gauss’s Law Faraday’s Law E B d l I B o J o o o enc t Ampere’s Law For Each of Maxwell’s Equations, you should have a simple picture in your mind. Gauss’s Law Qenc E da S o Ampere’s Law B d l I o enc Faraday’s Law d E dl dt B da Maxwell’s Equations in Vacuum B (i) (iii) E E 0 t E (iv) B o o B 0 (ii) t Take the curl of the curl, etc. B 2 ( E ) ( E ) E ( ) t E ( B) o o 2 t t 1 E 2 E 2 2 c t 2 And, you know who said, “Let There Be Light!” Introduction to Electrodynamics Chapter 1 Vector Analysis Chapter 2 Electrostatics Chapter 3 Special Techniques Vector Analysis Differential Calculus Integral Calculus Curvilinear Coordinates The Dirac Delta Function The Theory of Vector Fields The Electric Field Divergence and Curl of Electrostatic Fields Electric Potential Work and Energy in Electrostatics Conductors Laplace’s Equation The Method of Images Separation of Variables Multipole Expansions Chapter 4 Electric Fields in Matter Polarization The Field of a Polarized Object The Electric Displacement Linear Dielectrics Chapter 5 Magnetostatics The Lorentz Force Law The Biot Savart Law The Divergence and Curl of B Magnetic Vector Potential Chapter 6 Magnetic Fields in Matter Magnetization Field of a Magnetized Object Auxiliary Field H Linear and Nonlinear Media Chapter 7 Electrodynamics Electromotive Force Electromagnetic Induction Maxwell’s Equations











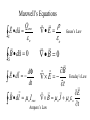







![Physics 431: Electricity and Magnetism [.pdf] (Dr. Tom Callcott)](http://s1.studyres.com/store/data/008774277_1-66222afe36519fd20b954143a2878995-150x150.png)









