* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Brief outline of types of construction:
Regular polytope wikipedia , lookup
Rational trigonometry wikipedia , lookup
Multilateration wikipedia , lookup
Golden ratio wikipedia , lookup
History of geometry wikipedia , lookup
Integer triangle wikipedia , lookup
Trigonometric functions wikipedia , lookup
Pythagorean theorem wikipedia , lookup
History of trigonometry wikipedia , lookup
Line (geometry) wikipedia , lookup
Area of a circle wikipedia , lookup
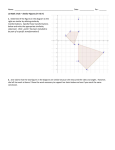
Carpenter’s Geometric Constructions Kevin Mirus Madison Area Technical College Madison East High School Math Week Monday, May 16, 2005 [email protected] http://www.matcmadison.edu/is/as/math/kmirus/ Page 1 of 17 1. The Pythagorean Theorem: a2 + b2 = c2 (for right triangles) Application: A triangle with sides of length 3, 4, and 5 (or multiples thereof) automatically forms a right triangle. This can be used to check that an angle is square, or to lay out a square angle. 2. Copying line lengths Problem: Construct a line segment congruent to a given segment. Given: Line segment AB Step 1: Choose any point C on line l. Step 2: Use a compass to measure the distance AB, then draw an arc centered at C with radius AB that intersects l at point D. Comments: This may seem overly simple, but it has a lot of practical uses. Application: Create an equilateral triangle, which has 60 angles. Problem: Construct an equilateral triangle. Comments: Application: You can use this to copy triangles, just by copying the lengths of each of the three sides. You can also use this to copy any polygon, since you can always divide it up into triangles. Page 2 of 17 3. Constructing Perpendicular Lines Application: To get the exact center of a distance without measuring, you can construct its perpendicular bisector: Problem: Construct the perpendicular bisector of a given line segment. Step 1: Draw arcs centered Step 2: Draw segment PQ . on A and B that have the Label its intersection with same radius greater than the AB as point M. distance to the midpoint. Label the intersections P and Q. Comments: Constructing the perpendicular bisector gives you both the midpoint and a right angle! Given: Line segment AB Problem: Construct a line perpendicular to a given line and through a given point. Starting with line segment AB and point C not on the line, strike an arc centered at C so that the arc intersects AB at two points (E and F). Construct the perpendicular bisector between EF, and it will pass through point C. Comments: Page 3 of 17 Application: This technique allows you to make squares and rectangles. Application: To find the center of a circle, pick any two random chords, then construct the perpendicular bisectors of the chords. The bisectors will intersect at the center of the circle. Problem: Locate the center of a given circle. Comments: Page 4 of 17 Application: Finding the center of an arch Page 5 of 17 Bisecting angles Problem: Construct the bisector of a given angle. Given: Angle BAC Step 1: Draw an arc of any radius centered at A. Label the points of intersection P and Q. Step 2: Draw arcs of equal radius from P and Q. The line from A through their intersection bisects BAC . Comments: Application: Making 45 and 22.5 angles from right angles, and making 30 and 15 angles from equilateral triangles. Page 6 of 17 4. Other regular polygons Application: Construct a regular pentagon. Problem: Construct a regular pentagon. Step 1 Step 2 Step 3 Step 4 Step 5 Step 6 Page 7 of 17 Step 7 Comments: s Problem: Construct a regular pentagon using a framing square. The distance from B to P is the length of each side of the pentagon. Comments: Page 8 of 17 Application: Construct a regular hexagon. Problem: Construct a regular hexagon. Just draw a circle, then mark the radius off six times around the circumference. Comments: This forms the basis for many a church window. Extending the pattern makes a pretty tiling. Application: Construct a regular Octagon… just make a square inside a circle, then bisect the angles. Or, construct 22.5 angles off of line segments until you get around the octagon. Page 9 of 17 5. Parallel Line construction Problem: Construct a line parallel to a given line through a point not on the given line. Given line AB, and point C not on the line, draw line AC. Then, strike a random-length arc centered at A that has intersection points D and E. Strike the same radius arc centered at C that has intersection point F. Use a compass to measure the distance from D to E, then mark off that same distance from point F to locate point G. The line through CG is parallel to AB. Comments: Problem: Construct a line parallel to a given line through a point not on the given line using the “draftsman's cheat”. Comments: Page 10 of 17 Problem: Partition a given line segment into a given number of congruent segments. To divide the original segment AB into 5 parts, draw a ray at any random angle, then mark it off in 5 equal parts until you get to point C. Draw a line through BC, then construct parallels to BC through each point on AC. The intersection points on AB will divide it into 5 equal parts. Comments: This is handy in carpentry for laying out stairs. Application: Use this construction to lay out evenly spaced stairs on a stringer. Page 11 of 17 Application: center line marking gauge Page 12 of 17 Application: corner round-over Page 13 of 17 Curves without strings Application: Construct a circle without a string or trammel. Problem: Draw a circle given its diameter using a framing square. Use the fact that an angle inscribed across a diameter is 90. Comments: This works better than a nail, string, and pencil. Application: An ellipse using a special trammel, and an approximate arc using a batten. Page 14 of 17 6. Special proportions Application: The Golden Ratio, as embodied in the Golden Rectangle, is the most pleasing rectangle and proportion to the human eye. The ratio of the length to 1 5 :1 1.618 :1 8 : 5 . Use it when designing the width of a Golden Rectangle is 2 furniture or buildings. Problem: Construct a Golden Rectangle. Start with square ABCD, then find the midpoint M of side CD. Strike an arc centered at M that starts at A and stops when it crosses ray CD (at point X). Construct point Y perpendicularly above point X, and the new rectangle BCXY is a golden rectangle. Comments: This is very useful in designing furniture with nice proportions. Page 15 of 17 Application: The Hambridge Progression is useful for designing chests of drawers where the drawers get shorter and shorter near the top of the dresser. Page 16 of 17 References 1. Tolpi, Jim, Measure Twice, Cut Once, Popular Woodworking Books, 1-55870428-0, 1996. 2. "Four Ways to Construct a Golden Rectangle," Fine Woodworking, Taunton Press, February 2004, No. 168, p. 50. 3. Isaacs, I. Martin, Geometry for College Students, Brooks/Cole Thomson Learning, 0-534-35179-4, 2001. 4. Posamentier, Alfred S. and William Wernick, Advanced Geometric Constructions, Dale Seymour Publications, 0-86651-429-5, 1988. 5. Martin, George E., Geometric Constructions, Springer, 0-387-98276-0, 1998. 6. Sykes, Mabel, Source Book of Problems for Geometry, Dale Seymour Publications, 0-86651-795-2, 1912. 7. Lundy, Miranda, Sacred Geometry, Wooden Books, 0-965-20578-9, 1998. 8. Bedford, John R., Graphic Engineering Geometry, Gulf Publishing Company, 087201-325-1, 1974. 9. Wingeom for Windows, website with freeware for geometric constructions (used to create all diagrams in this packet) http://math.exeter.edu/rparris/wingeom.html Page 17 of 17