Download Similar Polygons

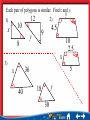
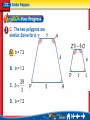
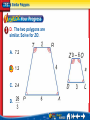
D. N. A.
1) Find the ratio of
BC to DG.
A B CD E F G
0
10
20
30
2) Solve each
proportion.
6 5
a) 
x 7
2x  3 4
b)

5x
3
Slides
Skills Practice
Practice
1, 4, 5
1-2
1-2
17, 21-27
3-6
3-6
Similar
Polygons
Chapter 7-2
• Identify similar figures.
• Solve problems involving scale factors.
• similar polygons
• scale factor
Standard 11.0 Students determine how changes in
dimensions affect the perimeter, area, and volume of
common geometric figures and solids.
Lesson 2 MI/Vocab
Similar Polygons
• Have congruent corresponding angles.
• Have proportional corresponding sides.
ABCD ~ EFGH
• “~” means “is similar to”
A  E
E
A
F
H
G
D
B
C
B  F
C  G
D  H
AB BC CD DA



EF FG GH HE
Writing Similarity Statements
• Decide if the polygons are similar. If they
are, write a similarity statement.
6
AB 6 3
A
A

W
 
WY 4 2
B  Y
15
BC 9 3
C  Z
 
YZ 6 2
D  X
12
CD 12 3
All corr. sides are D
 
4
ZX
8 2 proportionate and all W
DA 15 3
corr. angles are 
 
10
XW 10 2
ABCD ~ WYZX
X
8
B
9
C
Y
6
Z
Scale Factor
• The ratio of the lengths of two corresponding
sides.
• In the previous example the scale factor is 3:2.
Similar Polygons
A. Determine whether each pair of figures is similar.
Justify your answer.
The vertex angles are marked as 40º and 50º, so they
are not congruent.
Lesson 2 Ex1
Similar Polygons
Since both triangles are isosceles, the base angles in
each triangle are congruent. In the first triangle, the base
angles measure
and in the second
triangle, the base angles measure
Answer: None of the corresponding angles are
congruent, so the triangles are not similar.
Similar Polygons
B. Determine whether each pair of figures is similar.
Justify your answer.
All the corresponding angles are congruent.
Similar Polygons
Now determine whether corresponding sides are
proportional.
The ratios of the measures of the corresponding sides
are equal.
Answer: The ratio of the measures of the corresponding
sides are equal and the corresponding angles
are congruent, so ΔABC ~ ΔRST.
A. Determine whether the
pair of figures is similar.
A. Yes, ΔAXE ~ ΔWRT.
B. Yes, ΔAXE ~ ΔRWT.
C. No, the Δ's are not ~.
D. not enough information
B. Determine whether the
pair of figures is similar.
A. Yes, ΔTRS ~ ΔNGA.
B. Yes, ΔTRS ~ ΔGNA.
C. No, the Δ's are not ~.
D. not enough information
ARCHITECTURE An architect prepared a 12-inch
model of a skyscraper to look like a real 1100-foot
building. What is the scale factor of the model
compared to the real building?
Before finding the scale factor you must make sure that
both measurements use the same unit of measure.
1 foot = 12 inches
Answer: The ratio comparing the two heights is
or 1:1100. The scale factor is
means that the model is
, which
the height of the
real skyscraper.
Animation:
Similar Polygons
Each pair of polygons is similar. Find x and y.
1)
12
10
x
y
8
y
2)
4.5
9
10
2.5
x
3)
5
36
x
40
y
18
30
A space shuttle is about 122 feet in length. The
Science Club plans to make a model of the space
shuttle with a length of 24 inches. What is the scale
factor of the model compared to the real space
shuttle?
A.
B.
C.
D.
Proportional Parts and Scale Factor
A. The two polygons are similar.
Write a similarity statement. Then
find x, y, and UV.
Use the congruent angles
to write the corresponding
vertices in order.
polygon ABCDE ~ polygon RSTUV
Proportional Parts and Scale Factor
Now write proportions to find x and y.
To find x:
Similarity proportion
Cross products
Multiply.
Divide each side by 4.
Proportional Parts and Scale Factor
To find y:
Similarity proportion
AB = 6, RS = 4, DE = 8,
UV = y + 1
Cross products
Multiply.
Subtract 6 from each side.
Divide each side by 6 and
simplify.
Proportional Parts and Scale Factor
Proportional Parts and Scale Factor
B. The two polygons are similar.
Find the scale factor of polygon
ABCDE to polygon RSTUV.
The scale factor is the ratio
of the lengths of any two
corresponding sides.
Answer:
A. The two polygons are
similar. Write a similarity
statement.
A. TRAP ~ OZDL
B. TRAP ~ OLDZ
C. TRAP ~ ZDLO
D. TRAP ~ ZOLD
B. The two polygons are
similar. Solve for a.
A. a = 1.4
B. a = 3.75
C. a = 2.4
D. a = 2
C. The two polygons are
similar. Solve for b.
A. b = 7.2
B. b = 1.2
C.
D. b = 7.2
D. The two polygons are
similar. Solve for ZO.
A. 7.2
B. 1.2
C. 2.4
D.
E. The two polygons are
similar. What is the scale
factor of polygon TRAP to
polygon ZOLD?
A.
B.
C.
D.
1.
2.
3.
4.
A
B
C
D
Enlargement or Reduction of a Figure
Rectangle WXYZ is similar to rectangle PQRS with a
scale factor of 1.5. If the length and width of PQRS are
10 meters and 4 meters, respectively, what are the
length and width of rectangle WXYZ?
Write proportions for finding side measures. Let one long
side of each WXYZ and PQRS be
and one
short side of each WXYZ and PQRS be
Enlargement or Reduction of a Figure
WXYZ
PQRS
WXYZ
PQRS
Quadrilateral GCDE is similar to quadrilateral JKLM
with a scale factor of
. If two of the sides of GCDE
measure 7 inches and 14 inches, what are the lengths
of the corresponding sides of JKLM?
A. 9.8 in, 19.6 in
B. 7 in, 14 in
C. 6 in, 12 in
D. 5 in, 10 in
Scales on Maps
The scale on the map of a city is
inch equals 2
miles. On the map, the width of the city at its widest
point is
inches. The city hosts a bicycle race
across town at its widest point. Tashawna bikes at
10 miles per hour. How long will it take her to
complete the race?
Explore Every
equals 2 miles. The
distance across the city at its widest point is
Scales on Maps
Plan Create a proportion relating the measurements to
the scale to find the distance in miles. Then use
the formula
to find the time.
Solve
Cross products
Divide each side by 0.25.
The distance across the city is 30 miles.
Scales on Maps
Divide each side by 10.
It would take Tashawna 3 hours to bike across town.
Examine To determine whether the answer is
reasonable, reexamine the scale. If 0.25
inches = 2 miles, then 4 inches = 32 miles.
The distance across the city is approximately
32 miles. At 10 miles per hour, the ride would
take about 3 hours. The answer is reasonable.
Answer: 3 hours
An historic train ride is planned between two
landmarks on the Lewis and Clark Trail. The scale on
a map that includes the two landmarks is 3
centimeters = 125 miles. The distance between the
two landmarks on the map is 1.5 centimeters. If the
train travels at an average rate of 50 miles per hour,
how long will the trip between the landmarks take?
A. 3.75 hr
B. 1.25 hr
C. 5 hr
D. 2.5 hr
Forced Perspective
Using Ratios Example #1
• The Perimeter of a rectangle is 60 cm. The ratio of
AB:BC is 3:2. Find the length and width of the
A
B
rectangle.
3:2 is in lowest terms.
D
AB:BC could be
3:2, 6:4, 9:6, 12:8, etc.
AB = 3x Perimeter = l + w+ l + w
BC = 2x 60 = 3x + 2x + 3x + 2x
60 = 10x
L = 3(6) = 18
x=6
W = 2(6) = 12
C
Find the measures of the sides of each triangle.
12. The ratio of the measures of the sides of a
triangle is 3:5:7, and its perimeter is 450
centimeters.
13. The ratio of the measures of the sides of a
triangle is 5:6:9, and its perimeter is 220 meters.
14. The ratio of the measures of the sides of a
triangle is 4:6:8, and its perimeter is 126 feet.
Find the measures of the angles in each triangle.
15) The ratio of the measures of the angles is 4:5:6.
Using Ratios Example #2
• The angle measures in ABC are in the extended
ratio of 2:3:4. Find the measure of the three angles.
mA+ mB+ mC = 180o
Triangle Sum Thm.
2x + 3x + 4x = 180o
9x = 180o
B
4x
x = 20o
mA =
40o
mB = 60o
mC = 80o
A
2x
3x
C