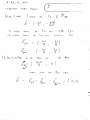Download .divxbhpi` ici lr dcyd z` aygp kdq d ~ E =

.divxbhpi` ici lr dcyd z` aygp
kdq
r̂
r2
dq = λdx
~ = kλ r̂dx
dE
r2
~ =
dE
.
z
oeeik ,il`icxd oeeika dcyd z` wxe j` epzi`n eywia
: `ed
r̂ẑ = cos θ =
r̂
ly
zd
aikxy ze`xdl xyt`
z
r
: okle
kλ z
kλz
kλz
dx = 3 dx =
3 dx
2
2
r r
r
(z + x2 ) 2
b
Z b
kλzx
√
dEz =
Ez =
z 2 z 2 + x2 −a
−a
b
a
kλ
√
+√
=
z
z 2 + b2
z 2 + a2
#
"
1
kλ
1
p
+p
=
z
1 + ( zb )2
1 + ( az )2
dEz =
:lawp ,seqpi`l mikled
Ez = 2
1
kλ
z
b
mbe
a
mb xnelk ,seqpi`l jled
L
y leaba
The electric field
Submitted by: I.D. 040460479
The problem:
An isolated electrical wire is charged uniformly with charge q and bent into a circular shape (radius
R) with a small hole b R (where b is the arc length).
What is the electrical field in the middle of the circle?
The solution:
The simple solution is to use superposition.
The electric field in the middle of a complete ring is, of course, zero.
Now we’ll sum up the field of a complete ring with the field of a very small wire of the same size
and shape as the hole but with a negative charge.
~ = kλb
x̂
Because b R the wire can be taken as a negative point charge and, therefore, the field is E
R2
q
(when we take the hole to be on the X axis and λ = 2πR ).
It is also possible to calculate the field directly. Taking ~r = (0, 0, 0) and ~r0 = (R cos θ, R sin θ, 0) we
have
kdq
(−R cos θ, −R sin θ, 0)
R3
dq = λRdθ
Z −α
kλ
kλRdθ0
~
(−R cos θ0 , −R sin θ0 , 0) =
(2 sin α, 0, 0)
E =
3
R
R
α
~ =
dE
(1)
(2)
(3)
where ±α are the angles of the edges of the bent wire (or, the upper and lower limits of the hole).
Since b R we can approximate tan α ' sin α = b/2
R .
Substituting into the expression for the field we obtain
~ = kλb x̂
E
R2
(4)
1
Energy of a disc and a rod
Submitted by: I.D. 040439358
The problem:
A disc of a radius R is charged uniformly with charge density σ. A rod of a length b is charged
uniformly with charge density λ. The rod is perpendicular to the disc (which is in the x − y plane)
and positioned on the axis of symmetry of the disc. The center of the rod is at z > 2b .
1. Calculate, from the direct integration of the field, the force between the objects.
The solution:
1. The force between the objects
Let ~r1 , ~r2 be the positions of charge elements on the disc and the rod, respectively.
~r1 = (r cos θ, r sin θ, 0)
(1)
~r2 = (0, 0, z)
(2)
~r = ~r2 − ~r1 = (−r cos θ, −r sin θ, z)
(3)
Because of the symmetry of the problem the force is in the z direction only. The electric field due
to the charge element dq on the disc is
dq z
r3
dq = σdA = σrdrdθ
(4)
dEz = k
(5)
The electric field of the disc is
Z R Z 2π
Z R
Z 2π
kσrdrdθz
rdr
Ez =
= kσz
dθ
3
3
0
0
0 (r 2 + z 2 ) 2 0
((r cos θ)2 + (r sin θ)2 + z 2 ) 2 )
Z R
z
rdr
1− √
= 2πkσz
3 = 2πkσ
R2 + z 2
0 (r 2 + z 2 ) 2
(6)
(7)
The force acting on the rod is
F~ =
Z
z+ 2b
z− 2b

Ez ẑλdz = 2πkσλ b +
s
R2 + z −
b
2
s
2
−
R2 + z +
The force acting on the disc is the same but in the opposite direction.
1
b
2
2

 ẑ
(8)