Download External reflections

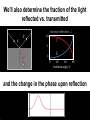
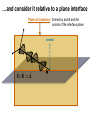
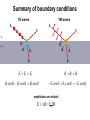
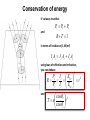
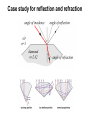
Chapter 23: Fresnel equations
Recall basic laws of optics
normal
i
Law of reflection:
i   r
Law of refraction
“Snell’s Law”:
sin  i  n2

sin  t  n1
r
n1
n2
t
Incident, reflected, refracted, and normal in same plane
Easy to derive on the basis of:
Huygens’ principle: every point on a wavefront may be regarded as a
secondary source of wavelets
Fermat’s principle:
the path a beam of light takes between two points is
the one which is traversed in the least time
Today, we’ll show how they can be derived
when we consider light to be an
electromagnetic wave
E and B are harmonic
 
 
E  E0 sin( k  r  t )
 
 
B  B0 sin( k  r  t )
Also, at any specified point in time and space,
E  cB
where c is the velocity of the propagating wave,
c
1
0 0
 2.998 108 m/s
We’ll also determine the fraction of the light
reflected vs. transmitted
external reflection, 
i
R
1.0
T
.5
T
R
0
0°
30°
60°
90°
Incidence angle, i
and the change in the phase upon reflection
Let’s start with polarization…
y
light is a 3-D vector field
z
x
linear polarization
circular polarization
…and consider it relative to a plane interface
Plane of incidence: formed by and k and the
normal of the interface plane
normal
 

E B  k
Polarization modes (= confusing nomenclature!)
always relative to plane of incidence
TE: transverse electric
s: senkrecht polarized
(E-field sticks in and out of the plane)
perpendicular (  ), horizontal
TM: transverse magnetic
p: plane polarized
(E-field in the plane)
parallel ( || ), vertical
Plane waves with k along z direction
oscillating electric field
y
y
x
x
Any polarization state can be described as linear combination of these two:

i kz t  y 
i  kz t  x 
ˆ
E  E0 x e
x  E0 y e
yˆ



i
E  E0 x eix xˆ  E0 y e y yˆ ei kz t 
“complex amplitude”
contains all polarization info
Derivation of laws of reflection and refraction
using diagram from Pedrotti3
boundary point
At the boundary point:
phases of the three waves must be equal:
 
 
 
(k i  r  it )  (k r  r  r t )  (k t  r  t t )
true for any boundary
point and time,

so let’s take r  0
 i t  r t  t t
or
i  r  t
hence, the frequencies are equal
t 0
 
 
 
ki  r  k r  r  kt  r
and if we now consider
which means all three propagation vectors lie
in the same plane
Reflection
 
 
 
ki  r  k r  r  kt  r
focus on first two terms:
 
 
ki  r  k r  r
ki r sin i  kr r sin  r
incident and reflected beams travel in
same medium; same l
ki  k r
hence we arrive at the law of reflection:
i   r
Refraction
 
 
 
ki  r  k r  r  kt  r
now the last two terms:
 
 
k r  r  kt  r
kr r sin  r  kt r sin t
reflected and transmitted beams travel in
different media (same frequencies;
different wavelengths!):
kr   / vr  n1 / c
kt   / vt  n2 / c
which leads to the law of refraction:
n1 sin  r  n2 sin t
Boundary conditions from Maxwell’s eqns
for both electric and magnetic fields, components parallel to
boundary plane must be continuous as boundary is passed
TE waves
electric fields: parallel to boundary plane

E 0i  Ei yˆ

E 0 r  Er yˆ

E 0t  Et yˆ
complex field
amplitudes
continuity requires:
Ei  Er  Et
Boundary conditions from Maxwell’s eqns
for both electric and magnetic fields, components parallel to
boundary plane must be continuous as boundary is passed
TE waves
magnetic fields:
 

i ( k i r t )
B i  ( B cos  i xˆ  B sin  i zˆ )e
 

i ( k r r t )
B r  ( B cos  r xˆ  B sin  r zˆ )e
 

i ( k t r t )
B t  ( B cos  t xˆ  B sin  t zˆ )e
continuity requires:
Bi cos  Br cos  Bt cos
same analysis can be performed for TM waves
Summary of boundary conditions

Ei
n1
n2
TE waves

Er

Bt

Bi

Ei
TM waves

Er

Bt 
Bi

Br

Et

Br

Et
Bi  Br  Bt
Ei  Er  Et
Bi cosi  Br cos r  Bt cost
 Ei cos i  Er cos  r   Et cos t
amplitudes are related:
E  vB   nc B
Fresnel equations
TE waves
TM waves
Get all in terms of E and apply law of reflection (i = r):
Ei  Er  Et
ni Ei  ni Er  nt Et
ni Ei cosi  ni Er cosi  nt Et cost
 Ei cosi  Er cosi   Et cost
For reflection: eliminate Et , separate Ei and Er , and take ratio:
cos  i  nnti cos  t
E
rTE  r 
Ei cos  i  nnti cos  t
rTM
E
 r 
Ei
nt
ni
nt
ni
cos  i  cos  t
cos  i  cos  t
Apply law of refraction ni sin i  nt sin t and let n 
rTE 
cos  i  n 2  sin 2  i
cos  i  n  sin  i
2
2
rTM 
nt
:
ni
n 2 cos  i  n 2  sin 2  i
n 2 cos  i  n 2  sin 2  i
Fresnel equations
TE waves
TM waves
For transmission: eliminate Er , separate Ei and Et , take ratio…
tTE
Et
2 cos  i


Ei cos  i  n 2  sin 2  i
tTM
Et
2n cos  i


Ei n 2 cos  i  n 2  sin 2  i
And together:
tTE  1  rTE
ntTM  1  rTE
Fresnel equations, graphically
External and internal reflections
External and internal reflections
occur when
external reflection:
n1  n2
internal reflection:
n1  n2
n2
n
1
n1
n2
n
1
n1
External reflections (i.e. air-glass)
n = n2/n1 = 1.5
RTM = 0
(here, reflected
light TE
polarized;
RTE = 15%)
at normal : 4%
1 n 
Rr 

1

n


2
normal
grazing
- at normal and grazing incidence, coefficients have same magnitude
2
- negative values of r indicate phase change


Pr
Er
2


R


r

- fraction of power in reflected wave = reflectance =

Pi
 Ei 
- fraction of power transmitted wave = transmittance = T 
 cos t  2
Pt
t
 n
Pi
 cos  i 
Note: R+T = 1
2
Glare
http://www.ray-ban.com/clarity/index.html?lang=uk
Internal reflections (i.e. glass-air)
n = n2/n1 = 1.5
total internal reflection
- incident angle where RTM = 0 is:  p
2
- both RTE  rTE2 and RTM  rTM
reach values of unity before =90°
 total internal reflection
 c  sin 1 (n)  sin 1
n2
n1
Internal reflections (i.e. glass-air)
Conservation of energy
it’s always true that
and
Pi  Pr  Pt
R T 1
in terms of irradiance (I, W/m2)
I i Ai  I r Ar  It At
using laws of reflection and refraction,
you can deduce
2
Pr I r  E0 r 
  r 2
R
  
Pi I i  E0i 
and
 cos t  2
t
T  n
 cos i 
Summary:
Reflectance and Transmittance for an
Air-to-Glass Interface
Perpendicular polarization
1.0
Parallel polarization
1.0
T
T
.5
.5
R
0
R
0
0°
30°
60°
Incidence angle, i
90°
0°
30°
60°
Incidence angle, i
90°
Summary:
Reflectance and Transmittance for a
Glass-to-Air Interface
Perpendicular polarization
1.0
Parallel polarization
1.0
R
R
.5
.5
T
T
0
0
0°
30°
60°
Incidence angle, i
90°
0°
30°
60°
Incidence angle, i
90°
Back to reflections
Brewster’s angle
or the polarizing angle
is the angle p, at which RTM = 0:  p  tan 1 n   tan 1
n2
n1
Brewster’s angle for internal and external reflections
at p, TM is perfectly transmitted
with no reflection
at Brewster’s angle, “s skips and p plunges”
s-polarized light (TE) skips off the surface; p-polarized light (TM) plunges in
Brewster’s angle
Punky Brewster
(1984-1986)
Sir David Brewster
(1781-1868)
Brewster’s other angles: the kaleidoscope
http://www.brewstersociety.com/cbs_sundaymorning_09.html
Phase changes upon reflection
-recall the negative reflection coefficients
-indicates that sometimes electric field
vector reverses direction upon reflection:
Er   r E
ip
  r E  e r E0e

i ( k r t )
 r E0e

i ( k r t p )
-p phase shift
external reflection: all angles for TE and at    p for TM
internal reflection: more complex…
Phase changes upon reflection: internal
in the region    c , r is complex
rTE 
rTM 
cos   i sin 2   n 2
cos   i sin 2   n 2
 n 2 cos   i sin 2   n 2
n 2 cos   i sin 2   n 2
reflection coefficients in polar form: r  r e
  phase shift on reflection
i
Phase changes upon reflection: internal
depending on angle of incidence, p    p
sin 2   n 2
 TE 
tan 

cos 
 2 
sin 2   n 2
 TM  p 
tan 

n 2 cos 
 2 
Exploiting the phase difference
circular polarization
-consists of equal amplitude components of
TE and TM linear polarized light, with
phases that differ by ±p/2
-can be created by internal reflections in a
Fresnel rhomb
each reflection
produces a π/4
phase delay
http://www.halbo.com/fr_rhmb.htm
Summary of phase shifts on reflection
external reflection
TE mode
TM mode
TE mode
TM mode
air
glass
internal reflection
air
glass
A lovely example
How do we quantify beauty?
Case study for reflection and refraction
Exercises
You are encouraged to solve
all problems in the textbook
(Pedrotti3).
The following may be
covered in the werkcollege
on 21 September 2011:
Chapter 23:
1, 2, 3, 5, 12, 16, 20