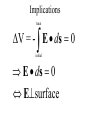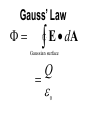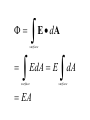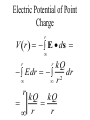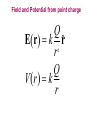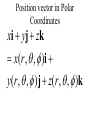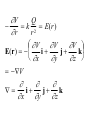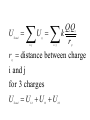Download r - Personal.psu.edu

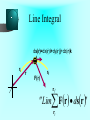
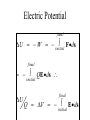
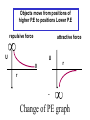
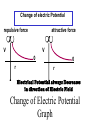
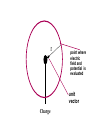
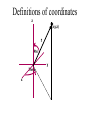
LESSON 25
Electric Potential
Definition
Comparison to Potential Energy
Equipotential Surfaces
Electric Potential due to point
charge
Electric Potential due to many
charge
Electric Potential Energy of
Interaction
Work done by a force F
on moving object from initial
point to final point
final
W
F

ds

initial
Line Integral
ds(r)=dx(r)i+dy(r)j+dz(r)k
ri
r
F(r)
rf
rf
"Lim Fr   dsr "
ri
Potential Energy
Work done by a conservative
force on an object is equal to
the negative of the change of
Potential Energy of the object
Thus equal to the change of
Kinetic Energy of the object
Capacitor
Electric Potential
final
 Fds
U   W   initial
final
 QEds 
  initial
U
final
 Eds
Q  V   initial
Electric Potential Difference
The change of electrical P.E.
per unit charge between an initial
point and a final point is called
the Potential Difference between
the points
It is the change of electric
potential between the two points.
Potentials at a point
By definition the P.E. at a
point infinite distance from the
source of a force is zero
Thus the electric potential at
a point infinite distance from
the source of an electric field
is zero
Electric
Potential
at
point
r
Formula
r
V r    E  ds

S.I. Units
[U]/[Q] = J/C= V (Volts)
Objects move from positions of
higher P.E to positions Lower P.E

repulsive force
U
attractive force
U
0
r
r
-

Change of PE graph
Change of electric Potential

repulsive force
V

attractive force
V
0
r
0
r
Electrical Potential always Decreases
in direction of Electric Field
Change of Electric Potential
Graph
Movement of Charge
Negative charge moves in
opposite direction to
electric field
Positive charge moves in
the same direction as an
electric field
Equipotential Surface
Equipotential Surface is
A connected set of points that
all have the same electric
potential
Potential Difference between
points is 0 volts.
Work done on Surface
No work is done when
moving charge from one to
point to another point on such
a surface
As change of P.E. between
points on surface is 0 Joules
Implications
final

V = - E  ds  0
initial
 E  ds  0
 Esurface
Field lines and Equipotential
Surfaces
+3C
-2C
Gauss’ Law
Review
of
Gauss'
Law
I
The Electric Flux through a surface
enclosing a charge is equal to the
Charge enclosed
divided by the
permittivity
The Electric Field outside of a
spherical charged object is the
same as if object were a point
charge
Gauss’
Law
Review of Gauss' Law II
E

dA


Gaussian surface

Q

0

Review of Gauss' Law III

E  dA
surface


EdA  E
surface
 EA

dA
surface
Implications
Surface of an isolated
conductor in electrostatic
equilibrium must be
an isopotential surface
Electric Potential of Point
Charge
r
V r     E  ds 

kQ
  Edr    2 dr
 r

r kQ
kQ


r
 r
r
r
Field and Potential from point charge
Electric Potential of Point
Charge IIQ
Er  k
r
Q
V r   k
r
2
rˆ
Picture
r
point where
electric
field and
potential is
evaluated
unit
vector
Charge
Polar Coordinates
V(r)  V(x, y, z) 
V(r,  ,  )  V(r)
Definitions of coordinates
z
(x,y,z)
r
Phi
y
Theta
x
Position vector in Polar
Coordinates
xi  yj  zk
 x(r,  ,  )i 
y(r,  ,  )j  z(r,  ,  )k
Electric Field and Potential
V
Q

for
k Point
 E(r
)
Charge
r
r2
 V
V
V 

E(r)  
i
j
k
 x
y
 z 
 V




i
j
k
x
y
z
radius of conductor
Graphs
= Electric
Potential
= Electric
Field
Magnitude
distance from center
of charged conductor
Spherical Charge
Electric Field and Electric
Potential outside of spherical
charged conductor is the
same as the field and
potential obtained from a
point charge that has the
same charge
Electric Potential due to
Electricmany
Potential
at a point due to
Sources
many source charges

r (r)
V(r )  V(r)dr= k
dr
  r
V(r0)  Vi (r0) 
i
i
Qi
k
r0 i
0
charged
body
charged
body
Potential Energy of
Potential Energy of
Interaction
Interaction I
Fixed source charge Q0 and fixed charge Q
F  QE
U  QV
Potential energy of interaction
between source charge of electric
field and the charge Q
Potential Energy of
Interaction II
P.E. of interaction between Q and Q0
(source charge) - positive work is done on
the charges in bringing them together if they
repel or negative work if they attract
If one brings another charge to a fixed
position work will be done (either positive or
negative) by the forces due to Q and Q0
U
Potential Energy of
Interaction III Q Q
Total


U 
ij
i j

i j
k
i
r
j
ij
r  distance between charge
ij
i and j
for 3 charges
U  U U U
Total
12
13
23