Download Lecture 08.v2.9-20-1..

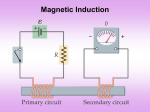
PHYS 1110
Lecture 8
Professor Stephen Thornton
September 20, 2012
Reading Quiz
A) move up
If there is a current in
B) move down
the loop in the direction
C) rotate clockwise
shown, the loop will:
D) rotate counterclockwise
E) both rotate and move
B field out of North
B field into South
N
S
N
S
Reading Quiz
A) move up
If there is a current in
B) move down
the loop in the direction
C) rotate clockwise
shown, the loop will:
D) rotate counterclockwise
E) both rotate and move
Look at the north pole: here the
F
magnetic field points to the right and
the current points out of the page.
N
S
The right-hand rule says that the force
must point up. At the south pole, the
same logic leads to a downward force.
Thus the loop rotates clockwise.
F
Discuss when Midterm Exam 1 will be.
Then determine homework 2 due date.
When would you prefer Exam 1?
A) Thursday, September 27
B) Tuesday, October 2
C) Thursday, October 4
Helical Motion
in a Magnetic
Field
Remember
F  qv  B
What happens if we form a loop
with the current carrying wire?
• Do demo with wire loop in magnetic field B.
(galvanometer demo)
• We find that the
loop rotates in
opposite directions
depending on the
direction of the
current!
Magnetic Forces on a Current Loop
F 0
I
I
F = IhB
Forces cause
a torque
F 0
Ftotal = 0
I
F  I LB
Magnetic Torque on a Current Loop
Top view


r
r

Wires affected
are into screen

F=IhB
Area = A = hw
Wire: width w
height h
F  I LB
Torque 
  r F
   left   right
  IhBw / 2  IhBw / 2
  IhwB  IAB
  IAB sin 
(if at angle)
Magnetic Force on Current Loops
• Consider a rectangular loop in a constant
magnetic field. Can also have N loops.
• Can easily find the force on each side of the loop
• Forces cancel but, depending on orientation,
there may be a torque
We define the magnetic
dipole moment of the
coil to be   IA  NIA.
Loop
Magnetic Torque on a Current Loop
We showed the torque to be   IAB sin 
We can rewrite this in vector form to be
B  N I A  B    B
where we have used N loops and the
magnetic dipole moment,   N I A.
Potential Energy of Magnetic Dipole
We can show (but not going to do) that
the potential energy of a magnetic dipole
moment in a magnetic field is
UB    B
Magnetic Torque on a Current Loop
Loop
of wire
A

B  N I A  B
 B  0
The torque rotates loop until
vectors A and  are parallel to B.
Galvanometer
A galvanometer takes
advantage of the
torque on a current
loop to measure
current; the spring
constant is calibrated
so the scale reads in
amperes. Remember
that all analog
ammeters use a
galvanometer.
Copyright © 2009 Pearson Education, Inc.
An electric motor uses the torque on a
current loop in a magnetic field to turn
magnetic energy into kinetic energy.
Do electric motor demo
Copyright © 2009 Pearson Education, Inc.
Conceptual Quiz
A) left
A vertical wire carries a current
B) right
and is in a vertical magnetic field.
C) zero
What is the direction of the force
D) into the page
on the wire?
E) out of the page
I
B
Conceptual Quiz
A vertical wire carries a current
and is in a vertical magnetic field.
What is the direction of the force
on the wire?
A) left
B) right
C) zero
D) into the page
E) out of the page
I
When the current is parallel to
the magnetic field lines, the force
on the wire is zero.
B
F= I ´ B
Hans Oersted, a Danish physicist, discovered this in
1820 while entertaining students and friends at
home. He was preparing a physics lecture.
Experimental observation
0I
shows B 
2 r
for a long straight wire
Now we can imagine combining
some of these effects.
• We know that a current carrying wire
produces a magnetic field.
• We also know that a current carrying
wire feels a force in a magnetic field.
• If we have two wires, can we use one
wire to produce a magnetic field at the
position of the second wire? Yes!
• If the second wire carries a current,
then it should feel a force!
• Do demo – next slide.
F2  I2  B1
We have to look closely at fields and
forces to see how the forces occur.
We do this
experiment to
show that
current
carrying wires
exert forces on
each other.
Magnetic field due to
current moving through
a coil of wire.
Note similarity between B of a bar magnet and B
of a coil of wire.
The Solenoid
B=0nI
MRI:
Magnetic
Resonance
Imaging
Induced EMF
Almost 200 years ago, Michael Faraday
looked for evidence that a magnetic field
would induce an electric current with this
apparatus:
Copyright © 2009 Pearson Education, Inc.
Do demos about induced currents.
Push and pull magnet in and out of coils
of wire to show current production.
Induced Current Produced by a Moving Magnet
v
v
Induced EMF
Therefore, a changing magnetic field induces
an emf/current.
Faraday’s experiment used a magnetic field
that was changing because the current
producing it was changing; the previous
graphic shows a magnetic field that is
changing because the magnet is moving.
Copyright © 2009 Pearson Education, Inc.
Magnetic Induction
B linked by
iron bar.
ind
We conclude that it is the change in magnetic
flux that causes induced current. F B = B A
Faraday’s Discovery and
the Law of Induction
There are many ways to change the
magnetic flux through a surface:
• Move the magnet
• Turning current on or off in one loop
induces current in another
• Move the loop
• Change the shape (and the area) of the
loop
The Magnetic Flux Through a Loop
Flux is maximum
Flux is zero.
 B  B  A magnetic flux
 B  BA cos
Look at the mathematics.
This is called Faraday’s Law of Induction
after Michael Faraday.
Induced emf 
 B
 N
t
N is number of turns
Don't worry about the sign. We will
have a better way to find this later.
Do some more demos.
1) Magnet through coil again.
2) Flash bulb
3) LED coil
Lenz’s Law
The induced current will
always be in the direction to
oppose the change that
produced it.
Induced emf Û Induced current
Applying Lenz’s Law to a Magnet Moving
Toward and Away From a Current Loop
Induced
current
v
v
Conceputal Quiz
In order to change
the magnetic flux
through the loop,
what would you
have to do?
A) drop the magnet
B) move the magnet upwards
C) move the magnet sideways a lot
D) Only A and B
E) A, B, and C
Conceptual Quiz
In order to change
the magnetic flux
through the loop,
what would you
have to do?
A) drop the magnet
B) move the magnet upwards
C) move the magnet sideways a lot
D) only A and B
E) A, B, and C
Moving the magnet in any direction would
change the magnetic field through the
loop and thus the magnetic flux.
Conceptual Quiz
If a North pole moves
toward the loop from above
the page, in what direction is
the induced current?
A) clockwise
B) counterclockwise
C) no induced current
Conceptual Quiz
If a North pole moves toward
the loop from above the page,
in what direction is the
induced current?
A) clockwise
B) counterclockwise
C) no induced current
The magnetic field of the moving bar
magnet is pointing into the page and
getting larger as the magnet moves
closer to the loop. Thus the induced
magnetic field has to point out of the
page. A counterclockwise induced
current will give just such an induced
magnetic field.
Follow-up: What happens if the magnet is stationary but the loop moves?
Motional emf
What
happens
when
we push
rod
down?
Determining the Direction of an Induced Current
We exert
force to push
bar down.
Motional emf
D F B = BD A = B vD t
e
DF B
B vD t
=
=
= B v
Dt
Dt
V = e= E
e= B v= E
E= B
e
B v
I= =
R
R
Find force and energy
2
B v
Bv
F I B
B
R
R
2 2 2
Bv
Pmechanical  Fv 
R
2
Pelectrical
2
Bv
 Bv 
 I R
 R
R
 R 
2
2 2 2
Conceputal Quiz
A wire loop is being
pulled through a
uniform magnetic field.
What is the direction of
the induced current?
A) clockwise
B) counterclockwise
C) no induced current
x x x x x x x x x x x x
x x x x x x x x x x x x
x x x x x x x x x x x x
x x x x x x x x x x x x
x x x x x x x x x x x x
x x x x x x x x x x x x
x x x x x x x x x x x x
Conceptual Quiz
A wire loop is being
pulled through a
uniform magnetic field.
What is the direction of
the induced current?
A) clockwise
B) counterclockwise
C) no induced current
x x x x x x x x x x x x
x x x x x x x x x x x x
Since the magnetic field is uniform, the
x x x x x x x x x x x x
magnetic flux through the loop is not
x x x x x x x x x x x x
changing. Thus no current is induced.
x x x x x x x x x x x x
x x x x x x x x x x x x
x x x x x x x x x x x x
Follow-up: What happens if the loop moves out of the page?
Conceptual Quiz
A conducting rod slides on a
conducting track in a constant
A) clockwise
B field directed into the page.
B) counterclockwise
What is the direction of the
C) no induced current
induced current?
x x x x x x x x x x x
x x x x x x x x x x x
x x x x x x x x x x x
x x x x x x x x x x x
v
Conceptual Quiz
A conducting rod slides on a
conducting track in a constant
A) clockwise
B field directed into the page.
B) counterclockwise
What is the direction of the
C) no induced current
induced current?
The B field points into the page.
The flux is increasing since the
area is increasing. The induced
B field opposes this change and
therefore points out of the page.
Thus, the induced current runs
counterclockwise, according to
the right-hand rule.
x x x x x x x x x x x
x x x x x x x x x x x
x x x x x x x x x x x
v
x x x x x x x x x x x
Follow-up: What direction is the magnetic force on the rod as it moves?
Electric Generators
A generator is the opposite of a motor – it
transforms mechanical energy into electrical
energy. This is an ac generator:
The axle is rotated by an
external force such as
falling water or steam.
The brushes are in
constant electrical
contact with the slip
rings. See next slide.
Copyright © 2009 Pearson Education, Inc.
An Electrical Generator
Current is
induced
Produces
AC power
Falling water,
steam
Magnetic flux
changes!
A Simple Electric Motor/Generator
Do demo
If the loop is rotating with constant angular
velocity ω, the induced emf is sinusoidal:
D
e = - BA D t (cos wt ) = BAw sin wt = e
For a coil of N loops,
e = NBAw sin wt
e = e sin wt
e = NBAw
0
0
Induced power:
e
P = eI =
R
Copyright © 2009 Pearson Education, Inc.
2
2
=
(NABw)
R
sin 2 wt
Conceptual Quiz
A generator has a coil of
wire rotating in a
magnetic field. If the
rotation rate increases,
how is the maximum
output voltage of the
generator affected?
A) increases
B) decreases
C) stays the same
D) varies sinusoidally
Conceptual Quiz
A generator has a coil of
wire rotating in a
magnetic field. If the
rotation rate increases,
how is the maximum
output voltage of the
generator affected?
The maximum voltage is the leading
term that multiplies sin(wt) and is
given by 0 = NBAw. Therefore, if
w increases, then 0 must increase
as well.
A) increases
B) decreases
C) stays the same
D) varies sinusoidally
  NBAw sin( wt )
Conceptual Quiz:
Look at the demonstration of the large
electromagnet. Observe what happens
(spark) when the switch is opened. What best
explains this?
A) The battery voltage is leaking through.
B) The steady current passing through the
magnet.
C) Induces a large back current (back emf).
D) V   in this case.
Answer: C
Nature doesn’t want the magnetic
flux to change, so it induces a large
current (back emf) to produce a
magnetic field. This emf results in
the spark across the switch.
Inductance and Inductors
• Faraday’s Law: Changing current
in a circuit will induce emf in that
circuit as well as others nearby
• Self-Inductance: Circuit induces
emf in itself (source of back emf)
• Mutual Inductance: Circuit
induces emf in second circuit
Inductance
 B  LI magnetic flux depends on current

 B
I

 L
t
t
L is called inductance (actually self inductance here).
The inductance L is a proportionality
constant that depends on the geometry
of the circuit
Changing Current
in an Inductor
Switch open. No current
flowing.
Switch closed. Inductor
opposes magnetic flux
change. Induces current
to oppose battery
current; current rises
more slowly.
Inductor
Magnetic field energy
We know that a battery has to do work to cause current
to flow. Similarly an inductor has to do work to cause
an induced current to flow from 0 to I in time T. This
energy comes from the magnetic field.
I LI
 L 
t T
1
1 LI 2
Pav  I avV  I  
2
2 T
1 2
U  PavT  LI  W
2
The work W done is the
energy U stored in the inductor
1 2
U  LI
2
There will be a magnetic flux in Loop 1 due to current I1
flowing in Loop 1 and due to current I2 flowing in Loop 2.
 B (1)  L1I1  M12I2
Similarly,
 B (2)  L2I2  M 21I1
Now it is clearer why we
call L self inductance and
M mutual inductance.
For example, two
nearby coils
Mutual Inductance
A long thin solenoid of length ℓ and cross-sectional area
A contains N1 closely packed turns of wire. Wrapped
around it is an insulated coil of N2 turns. All the flux from
coil 1 (the solenoid) passes through coil 2. The
magnetic flux between the two coils is linked. We call
this mutual inductance.
Copyright © 2009 Pearson Education, Inc.
Unit of inductance: the henry, H:
1 H = 1 V·s/A = 1 Ω·s.
A transformer is an
example of mutual
inductance.
Copyright © 2009 Pearson Education, Inc.
Area A
Solenoid Self-Induction
B  0 nI
 B  NBA  0 nNIA  0 An 2 I
 B  LI , so L  0 An 2
Only depends on geometry.
Consider an inductor
For a solenoid
L  0 n A
2
1 2 1
1
2
2
2 2 2
U  LI   0 n A  I 
( 0 n I ) A
2
2
2 0
1 2
1 2
But B  0 nI , so U B 
B A 
BV
2 0
2 0
2
magnetic energy B
uB 

volume
2 0
energy density
General energy density
2
1B
uB 
2 0
general result
1
2
uE   0 E
2
1 B
2
u  uB  uE  
 0E 
2  0

2
We can produce an emf by
using AC voltage and coils.
Show demo of AC coils and light bulb
Do transformer demo
Transformer equation
Primary coil:

Secondary coil:
P
 NP

S
 P
t
 S
 NS
t
For good transformer,  P   S

and

P
S

NP
NS
VP N P
If resistance is small,

VS N S
 NS 
VS  VP 

 NP 
step-up and step-down transformers
This is a step-up
transformer – the
emf in the secondary
coil is larger than the
emf in the primary:
Copyright © 2009 Pearson Education, Inc.
Lots of applications for transformers,
the bug zapper.
Power distribution
Transformers work only if the current is
changing; this is one reason why electricity is
transmitted as ac.
Conceptual Quiz
A) 30 V
What is the voltage
B) 60 V
across the lightbulb?
C) 120 V
D) 240 V
E) 480 V
120 V
Conceptual Quiz
A) 30 V
What is the voltage
B) 60 V
across the lightbulb?
C) 120 V
D) 240 V
E) 480 V
The first transformer has a 2:1 ratio
of turns, so the voltage doubles.
But the second transformer has a
1:2 ratio, so the voltage is halved
again. Therefore, the end result is
the same as the original voltage.
120 V
240 V
120 V
Conceptual Quiz
A 6 V battery is connected to one
A) greater than 6 V
side of a transformer. Compared
B) 6 V
to the voltage drop across coil A,
C) less than 6 V
the voltage across coil B is:
D) zero
A
6V
B
Conceptual Quiz
A 6 V battery is connected to one
A) greater than 6 V
side of a transformer. Compared
B) 6 V
to the voltage drop across coil A,
C) less than 6 V
the voltage across coil B is:
D) zero
The voltage across B is zero.
Only a changing magnetic flux
induces an emf. Batteries can
provide only dc current.
A
6V
B