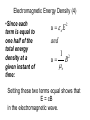Download 23.5 Semiconductor Devices

Semiconductors and Electromagnetic Waves
23.5 Semiconductor Devices
Semiconductor devices such as diodes and transistors are widely
used in modern electronics.
“Technology has clearly revolutionized society, but solid-state
electronics is revolutionizing technology itself”.
Semiconductors
•Silicon is the most
common material used
as a semiconductor
(germanium is also
used).
•It has 4 valence
electrons and forms a
stable lattice structure.
•All electrons are used in
the bonding process of
the lattice, there are none
free to move through the
lattice structure, therefore
pure Si is a poor
conductor.
23.5 Semiconductor Devices
SEMICONDUCTORS
The semiconducting materials (silicon and germanium)
used to make diodes and transistors are doped by
adding small amounts of an impurity element.
23.5 Semiconductor Devices
n-TYPE SEMICONDUCTORS
•Small amounts of a material
with 5 outer-shell electrons
added to the silicon (e.g
phosphorus).
•Extra electron which diffuses
through the silicon lattice
structure and increases overall
conductivity.
•The n-type semiconductor is
electrically neutral. Although the
phosphorus contributed an
electron that doesn’t fit into the
lattice structure, the phosphorus
atom is neutral.
23.5 Semiconductor Devices
p-TYPE SEMICONDUCTORS
•Small amounts of a material with 3 valence electrons are added to the
silicon (e.g boron). This leaves an electron “hole” which diffuses
through the silicon lattice structure and increases conductivity.
•Note that the p-type semiconductor is electrically neutral, just like the
n-type material.
23.5 Semiconductor Devices
What do you get when you put an p-type
and an n-type semiconductor together?
overall neutral
overall neutral
You get a p-n Junction
• Mobile electrons from the blue, n-type material move left to
fill the holes in the pink p-type material ( left, in Fig a). One
may think of the square electron holes as moving right.
•The layer at the end of p-type material becomes negative
and vice versa. This results in an electric field, pointing
from n-type material to p-type material (Fig b).
•The resulting structure is called a diode.
•No current flows because the diode is electrically neutral.
Connect a voltage source with a diode.
Consider attaching a battery so that positive terminal (gold) goes to the n-type
side and the negative terminal goes to the p-type side. What happens?
a. Current flows in the direction of the E field (left).
b. Current flows against the electric field (right)
c. Current doesn’t flow
Connect a voltage source with a diode.
Consider attaching a battery so that positive terminal (gold) goes to the n-type
side and the negative terminal goes to the p-type side. What happens?
a. Current flows in the direction of the E field (left).
b. Current flows against the electric field (right)
c. Current doesn’t flow, the positive charge is repelled by the positive layer
in the n-type material.
23.5 Semiconductor Devices
There is an appreciable current through the diode when the
diode is forward biased.
Under a reverse bias, there is almost no current through the
diode.
23.5 Semiconductor Devices
•The graph shows
dependence of current on
magnitude and polarity of
voltage applied across an
ideal p-n junction.
•the arrow/bar is the
symbol for diode (arrow
shows the direction the
diode allows conventional
current to flow).
•Reverse bias- regardless
of how much voltage
applied, no current flows.
•Forward bias – after
some “threshold” voltage
applied (here slightly
more than 0.5 volts),
current rises at an
exponential rate.
23.5 Semiconductor Devices
•A more realistic graph for a silicon
diode.
•When reverse-biased, a real diode
lets in a very small amount of current.
•If you apply enough reverse voltage
(V), the junction breaks down and lets
current through (shown at far-left
unlikely in normal circumstances).
•When forward-biased, the threshold
voltage for silicon is about 0.7 volts.
•A diode is a non-ohmic device; it does
not obey Ohm’s Law.
•If you apply more more voltage
(bigger battery), the current through
the diode will increase, but the voltage
drop will always remain at the
threshold value.
A solar cell is a diode.
•Photons in sunlight hit the
solar panel.
•The energy ionizes atoms in
the charge layers.
•Electrons are ejected from
their atoms, allowing them to
flow through the material to
produce electricity.
•Due to the composition of
solar cells, the electrons are
only allowed to move in a
single direction. As a result,
the solar cell develops a
positive and negative terminal,
much like a battery.
24.1 The Nature of Electromagnetic Waves
This picture shows an electromagnetic wave, such as a light wave, or
radio wave
An EM wave is a transverse wave that does not need a medium, e.g. air,
or water, to propagate.
• In 1865, long before the experiment, the English physicist
Maxwell correctly predicted that, in a vacuum:
ε0 = 8.85 x 10-12 C2/(N m2
μ0 = 4π x 10-7 T m/A.
c
1
 0 0
24.3 The Speed of Light
•The American physicist
Albert Michaelson
improved on attempts to
measure the speed of
light.
•By placing his mirrors on
top of 2 Southern
California mountains, he
obtained a value of c that
was less than 0.0014%
different that the currently
accepted value.
•He definitely got a A on
that lab.
c  3.00 10 m s
8
24.2 The Electromagnetic Spectrum
Like all waves, electromagnetic waves have a wavelength and
frequency, related by:
c  f
24.2 The Electromagnetic Spectrum
Example 1 The Wavelength of Visible Light
Find the range in wavelengths for visible light in the frequency range
between 4.0x1014Hz (red) and 7.9x1014Hz (violet).
c 3.00 108 m s
7
 

7
.
5

10
m  750 nm
14
f
4.0 10 Hz
c 3.00 108 m s
7
 

3
.
8

10
m  380 nm
14
f
7.9 10 Hz
The Crab Nebula is a remnant of a star that underwent a
supernova. This event was recorded in the year 1054 A.D (see
Anasazi pictograph, below). The Crab Nebula is located at a
distance of 6.0 x 1016 km away from the earth. How long ago did
the supernova happen?
The Crab Nebula is a remnant of a star that underwent a
supernova. This event was recorded in the year 1054 A.D (see
Anasazi pictograph, below). The Crab Nebula is located at a
distance of 6.0 x 1016 km away from the earth. How long ago did
the supernova happen? - 7300 years ago from 2010
24.4 The Energy Carried by Electromagnetic Waves
Electromagnetic waves, such as the microwaves
shown below, carry energy, much like sound waves
Light waves and infrared rays
also carry energy
Greenhouse gases
•A greenhouse gas
(sometimes abbreviated
GHG) is a gas in an
atmosphere that absorb and
emit radiation in the thermal
infrared part of the spectrum
•Greenhouse gases (CO2,
CH4 H2O) in the atmosphere
absorb infrared radiation and
then re-emit it in all directions
• Most solar energy is in the form of shortwave radiation (e.g. light, uv
rays)
• Earth absorbs this energy and re-emits as longwave radiation (infrared, “heat”)
• Greenhouse gases (CO2, CH4 H2O) in the atmosphere absorb
infrared radiation
• This natural process allows the Earth to maintain an average yearly
temperature of about 150 C (600 F).
Electromagnetic Energy Density (0)
•Electromagnetic waves fluctuate in a sinusoidal
manner. When the electric field has a maximum
strength, so does the magnetic field. Both are zero at
the same instant.
•The energy carried by the wave fluctuates in the
same manner.
•A way to quantify the energy of an electromagnetic
wave is to measure the total energy density carried by
an electromagnetic wave (energy per unit volume).
Electromagnetic Energy Density (1)
•This can be divided into electric energy density and
magnetic energy density:
electric energy 1
2
 oE
Volume
2
•where E is the magnitude of the electric field at some
instant, and ε0 = 8.85 x 10-12 C2/(N m2 )
Electromagnetic Energy Density (2)
•Similarly, the magnetic energy density is:
magnetic energy
1 2

B
Volume
2o
•where B is the magnitude of the magnetic field at
some instant and μ0 = 4π x 10-7 T m/A.
• In 1865, long before Michelson’s experiment, the
English physicist Maxwell correctly predicted that:
c
1
 0 0
Electromagnetic Energy Density (3)
•The total energy density is a combination of the
electrical energy stored in the electric field and the
magnetic energy stored in the magnetic field.
Total energy 1
1 2
2
u
 oE 
B
Volume
2
2o
•This value changes as the electric and magnetic
fields fluctuate.
Electromagnetic Energy Density (4)
•Since each
term is equal to
one half of the
total energy
density at a
given instant of
time:
u  oE
2
and
u
1
o
B
2
Setting these two terms equal shows that
E = cB
in the electromagnetic wave.
Average energy density and rms values
•The energy density fluctuates between zero and some
maximum value, when E and B are at their maximum
values.
•To obtain an average value of energy density, we use
rms (root mean square) values for E and B in the
calculations:
1
1
E0 and B =
B0
Erms =
rms
2
2
Example
The rms value of the magnetic field in an
electromagnetic wave is 3.3 x 10-6 T.
a. What is the maximum strength of the
wave’s electric field?
b. What is the average energy density, u, of
the wave?
Example
The rms value of the magnetic field in an
electromagnetic wave is 3.3 x 10-6 T.
a. What is the maximum strength of the
wave’s electric field? 1400 V/m
b. What is the average energy density, u, of
the wave? 8.67 x 10-6 J/m3.
EM Wave Intensity
•Intensity – defined
previously for sound
waves as power to area
ratio: Intensity = P/A.
•Intensity is inversely
proportional to the
square of the distance
from the source of the
wave.
•Recall power is the
amount of energy
transported per second.
EM Wave Intensity
Note the volume through which the energy passes is
ctA, and your book uses S for intensity
P Total energy uctA
S 

 cu
A
tA
tA
EXAMPLE The electric field of
a laser beam
Note that a laser sends out light in a fixed beam, not out in
all directions, so the appropriate area to use is the area of
the circular beam, and not the surface area of a sphere.
EXAMPLE The electric field of a laser
beam
I
u
c
and
u  oE
2
therefore
and
2
1270W/m
1 2
E
 x1012BC2 /Nm2 )
(3.0 x108 m/s )(u8.85
o
I
c 0
E
= 690 V/m
24.5 The Doppler Effect and Electromagnetic Waves
Electromagnetic waves also can exhibit a Dopper effect, but it
differs for two reasons:
a) Sound waves require a medium, whereas electromagnetic
waves do not.
b) For sound, it is the motion relative to the medium that is important.
For electromagnetic waves, only the relative motion of the source
and observer is important.
 vrel 
f o  f s 1 

c 

if vrel  c
c) use plus if observer and source are moving together, minus if they
are moving apart.
d) vrel is a magnitude and therefore always positive.
24.5 The Doppler Effect and Electromagnetic Waves
Example 6 Radar Guns and Speed Traps
The radar gun of a police car emits an electromagnetic wave with a
frequency of 8.0x109Hz. The approach is essentially head on. The
wave from the gun reflects from the speeding car and returns to the
police car, where on-board equipment measures its frequency to be
greater than the emitted wave by 2100 Hz. Find the speed of
the car with respect to the highway. The police car is stationary.
24.5 The Doppler Effect and Electromagnetic Waves
source frequency
fs = 8 x 109 Hz
frequency “observed”
by speeding car
vrel vrel 
2100 Hz  f o  f s  f o  ff s (1 f 1  ) f s
o
s c
  c 
reflected frequency observed
by police car
 v 
f o  f o 1  rel 
c 

Replace f’0 with term for f0 on the right side of equation:
v 
f o  f s  f o (1   rel )  f s
 c 
Replace f0 with fs on the right side of the equation and expand the square:
 vrel   vrel 
( f o  f s )  f s 1 
 1 
  fs
c 
c 


2


v
v


rel
rel

  fs
( fo  f s )  f s 1  2




c
c





24.5 The Doppler Effect and Electromagnetic Waves
Continuing:
2


v
v



rel
rel

( fo  f s )  f s  2


 c  c  


vrel 
vrel 
( fo  f s )  f s
2 

c 
c 

but we can make the assumption that vrel<< c, so the last term becomes 2:
v

( f o  f s )  2 f s rel
c
 f o  f s   2100 Hz 
8
c  
vrel  
3
.
0

10
m s  39 m s

9
 2 f s   2 8.0 10 Hz 




Doppler weather radar uses the Doppler shift of
reflected radar signals to measure wind speeds
and gauge the severity of a storm.
This picture is off the coast of Florida.
Red shifts and blue shifts: The Big Bang
 v 
f o  f s 1  rel 
c 

•
•
•
•
For light coming from astronomical objects,
this Doppler equation is no longer correct,
but it is still true that the light coming from
an object moving closer has a higher
frequency, while the light coming from a
receding object has a lower frequency.
We say light has been “blue-shifted” for an
object moving closer, and “red-shifted” for
an object moving away.
The light coming from the stars and
galaxies around us is red-shifted, leading
to our present belief that the galaxy is
expanding.
Extrapolating back in time brings us to a
point when the universe was contained in a
volumeless point that “exploded”, aka The
Big Bang.
if vrel  c