Download PHYS_3342_091511

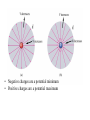
My office change was not reflected on the syllabus. It is now ESCN 2.206.
Our first exam is a week from next Tuesday - Sep 27. It will cover everything I have
covered in class including material covered next Thursday.
There will be two review sessions Monday, Sep 26 - at 12:30 PM and at 3:00 PM in
the same room as the problem solving session: FN 2.212.
I have put several (37) review questions/problems on Mastering Physics. These are
not for credit but for practice. I will review them at the review session Monday.
Potential of a point charge
Moving along the E-field lines means moving in the direction of
decreasing V.
As a charge is moved by the field, it loses potential energy, whereas if
the charge is moved by the external forces against the E-field, it
acquires potential energy
• Negative charges are a potential minimum
• Positive charges are a potential maximum
Positive Electric Charge Facts
• For a positive source charge
– Electric field points away from a positive source charge
– Electric potential is a maximum
– A positive object charge gains potential energy as it moves
toward the source
– A negative object charge loses potential energy as it moves
toward the source
Negative Electric Charge Facts
• For a negative source charge
– Electric field points toward a negative source charge
– Electric potential is a minimum
– A positive object charge loses potential energy as it moves
toward the source
– A negative object charge gains potential energy as it moves
toward the source
Electron Volts
Electron volts – units of energy
U  eVab
1 eV – energy a positron (charge +e) receives when it goes
through the potential difference Vab =1 V
Unit: 1 Volt= 1 Joule/Coulomb (V=J/C)
Field: N/C=V/m
1 eV= 1.6 x 10-19 J
Just as the electric field is the electric force
per unit charge, the electrostatic potential is
the potential energy per unit charge.
Clicker question
There is a 12 V potential difference between the positive and negative ends of a
set of jumper cables, which are a short distance apart. An electron at the
negative end ready to jump to the positive end has a certain amount of potential
energy. On what quantities does this electrical potential energy depend?
a. the distance and the potential difference between the ends of the cables
b. the distance and the charge on the electron
c. the potential difference and the charge
d. the potential difference, charge, and distance
Assume that two of the electrons at the negative terminal have attached
themselves to a nearby neutral atom. There is now a negative ion with a charge
at this terminal. What are the electric potential and electric potential energy of
the negative ion relative to the electron?
a. The electric potential and the electric potential energy are both twice as much.
b. The electric potential is twice as much and the electric potential energy is the
same.
c. The electric potential is the same and the electric potential energy is twice as
much.
d. The electric potential and the electric potential energy are both the same.
e. The electric potential is the same and the electric potential energy is increased
by the mass ratio of the oxygen ion to the electron.
Examples
A small particle has a charge -5.0 mC and mass 2*10-4 kg. It moves
from point A, where the electric potential is fa =200 V and its speed
is V0=5 m/s, to point B, where electric potential is fb =800 V. What
is the speed at point B? Is it moving faster or slower at B than at A?
E
2
2
A
B
F
mV0
mV
 qa 
 qb
2
2
Vb ~ 7.4 m / s
In Bohr’s model of a hydrogen atom, an electron is considered
moving around a stationary proton in a circle of radius r. Find
electron’s speed; obtain expression for electron’s energy; find total
energy.
11
e2
V2
r

5.3

10
m
U
Fe  ke 2  m
K
r
r
2
T  13.6 eV
T  K U
Calculating Potential from E field
• To calculate potential function from E field
V   
f
i
r r
E  ds

   (E x iˆ  E y ˆj  E z kˆ )  dxiˆ  dyˆj  dzkˆ
f
i


f
i
E x dx  E y dy  E z dz

When calculating potential due to charge distribution, we calculate potential explicitly
if the exact distribution is known.
If we know the electric field as a function of position, we integrate the field.
b

   E d l
a
Generally, in electrostatics it is easier to calculate a potential (scalar) and then find
electric field (vector). In certain situation, Gauss’s law and symmetry consideration
allow for direct field calculations.
Moreover, if applicable, use energy approach
rather than calculating forces directly
(dynamic approach)
Example: Solid conducting sphere
Outside: Potential of the point charge
1
q
V
4 0 r
Inside: E=0, V=const
Potential of Charged Isolated Conductor
• The excess charge on an isolated conductor will distribute itself
so all points of the conductor are the same potential (inside and
surface).
• The surface charge density (and E) is high where the radius of
curvature is small and the surface is convex
• At sharp points or edges  (and thus external E) may reach high
values.
• The potential in a cavity in a conductor is the same as the
potential throughout the conductor and its surface
At the sharp tip (r tends to zero), large
electric field is present even for small
charges.
Lightning rod – has blunt
end to allow larger charge
Corona – glow of air due to gas discharge built-up – higher probability
near the sharp tip. Voltage breakdown of of a lightning strike
the air
Vmax  3  10
6
V /m
Vmax  REmax
Example: Potential between oppositely charged parallel plates
From our previous examples
U ( y )  q0 Ey
V ( y )  Ey
Vab
E
d
Easy way to calculate surface
charge density

 0Vab
d
Remember! Zero potential doesn’t mean the conducting object has no
charge! We can assign zero potential to any place, only difference in
potential makes physical sense
Example: Charged wire
We already know E-field around the wire
only has a radial component
b
1 
rb

ln
Er 
;    E  dr 
2 0 ra
2 0 r
a
Vb = 0 – not a good choice as it follows
Va  
Why so?
We would want to set Vb = 0 at
some distance r0 from the wire
r - some distance from the wire
r0

V
ln
2 0 r
Example: Sphere, uniformly charged inside through volume
r
q  Q 
R
R
3
'
E
Q - volume density of charge

V

r
3 0
R
 (r  R)
r
 R  r   E dr
2
R
k eQ r r
R    3
|R
R 2
keQ
R 
R
Q - total charge
k eQ 
r2 
r 
3  2 
2R 
R 
This is given that at infinity  0
Potential Gradient
b

 a  b   E  d l
We can calculate potential
difference directly
a
a
 a  b   d
b




E  i Ex  j E y  k Ez
Ex  

d  Ex dx  E y dy  Ez dz



: Ey  
: Ez  
x
y
z
E  
Components of E in terms of 
  operator "del"
Frequently, potentials (scalars!) are easier to calculate:
So people would calculate potential and then the field
Superposition for potentials: V = V1 + V2 + …
Example: A positively charged (+q) metal sphere of radius ra is inside
of another metal sphere (-q) of radius rb. Find potential at different points
inside and outside of the sphere.
a) r  ra : b)ra  r  rb : c)r  rb
1
-q
a)
2
V2 (r ) 
V1 (r ) 
+q
q
4 0rb
q
4 0ra
Total V=V1+V2
b)
Electric field between spheres
q 1 1
V (r ) 
  
4 0  r rb 

E
r
V (r ) 
c)
q 1 1
  
4 0  ra rb 
V 0