Download Presentation 3

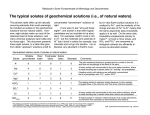
Soil Solution
Sampling
Soluble Complexes
Speciation
Thermodynamic Stability Constant
Extraction Methods
Collect drainage water in situ
Reaction with collection vessel
Must be at or near saturation
High variability
Displace with an immiscible liquid
As by F3Cl3C2 in centrifuge (ρ = 1.58 g cm-3)
Displace using air pressure (positive or vacuum)
Reaction with filter
Must be at or near saturation
Displace using centrifugal force
Generally, the extract cannot be identical to the true soil solution
Criticize this approach.
Particle density = 2.62 g cm-3 and bulk density = 1.32 g cm-3
so that porosity = 0.50. What is the composition of saturated
soil solution?
Equilibrate
10 g water + 1 g soil, centrifuge and analyze
5 g water + 1 g soil
5 g water + 5 g soil
10
5
1
0.37
Empirically model Ca2+, Mg2+, …, SO42-, … and extrapolate.
Soluble Complexes
Complex consists of a molecular unit (e.g., ion) as a center
to which other units are attracted to form a close association
Examples include Si(OH)4 and Al(OH)2+ with Si4+ and Al3+
as the central unit and OH- as ligands
If two or more functional groups of a ligand are coordinated
to a central metal, complex is called a chelate
If central unit and ligands are in direct contact, complex is inner-sphere
If one or more H2O in between, complex is outer-sphere
If ligands are H2Os, complex is solvation complex (e.g., Ca(H2O)62+)
What would be orientation of H2Os?
Mg2+(aq) + SO42-(aq) = MgSO4(aq)
Given that –COO- tends to form water bridges to soil minerals via
divalent cations adsorbed onto mineral surfaces, is the MgSO4
complex inner- or outer-sphere?
Kinetics of complex formation are fast
Assume described by rate of disappearance of the metal
as in the rate of its concentration decrease,
-d[Mg2+] / dt = Rf – Rr
where forward and reverse rates are affected by
the temperature, pressure and composition of the solution
Further, typically,
-d[Mg2+] / dt = kf [Mg2+]α[SO42-]β – kr[MgSO4]γ
αth order with respect to Mg2+
If tracked formation under conditions of excess SO42-,
could determine α
-d[A] / dt = kf [A]α
0th
- d[A] / dt = kf
and
1st
- d[A] / dt = kf[A]
and ln[A] = -kft + ln[Ao]
2nd
- d[A] / dt = kf[A]2
and 1/[A] = kft + 1/[Ao]
[A] = -kft + [Ao]
What if
-d[Mg2+] / dt = kf [Mg2+][SO42-] – kr[MgSO4]
at equilibrium
0 = kf [Mg2+][SO42-] – kr[MgSO4]
[MgSO4] / [Mg2+][SO42-] = kf / kr = cKs
Do problem 2.
Al3+ + F- = AlF2+
-d [Al3+] / dt = kf [Al3+][F-] – kr [AlF2+]
At early stage of reaction, ignore reverse rate and since initial concentrations
of Al3+ and F- are the same, [F-] = [Al3+], giving
-d [Al3+] / dt = kf [Al3+]2
or
-d [Al3+] / [Al3+]2 = kf dt
which integrates to
1 / [Al3+] – 1 / [Al3+]0 = kf t
Now what is the time when ½ of the Al3+ has reacted, i.e., the half life?
1 / ½ [Al3+]0 – 1/ [Al3+]0 = kf t½
t½ = (1 / kf) (1 / [Al3+]0)
or
= 909 s @ pH 3.9, given kf = 110 M-1 s-1
= 138 s @ pH 4.9, given kf = 726 M-1 s-1
Speciation Equilibria
Assumption of fast complex formation and slow redox / precipitation
Al speciation example
Limit possible ligands to SO42-, F- and fulvic acid (L-)
Set pH = 4.6 for which AlOH2+ is major hydroxide complex
Ignore polymeric forms of aluminum
[Al]T = [Al3+] + [AlOH2+] + [AlSO4+] + [AlF2+] + [AlL2+]
Use conditional stability constants to express concentrations in terms of
[Al3+], [OH-] or [H+] and concentrations of ligand species
[AlOH2+] = cK1 [Al3+][OH-]
[AlSO4+] = cK2 [Al3+][SO42-]
[AlF2+] = cK3 [Al3+][F-]
[AlL2+] = cK4 [Al3+][L-]

[Al]T = [Al3+] { 1 + cK1 [OH-] + cK2 [SO42-] + cK3 [F-] + cK4 [L-]}
Similarly,
[SO42-]T = [SO42-] { 1 + cK2 [Al3+]}
[F-]T = [F-] { 1 + cK3 [Al3+]}
[L-]T = [L-] { 1 + cK4 [Al3+]}
Now proceed iteratively,
Step 1 begin
[Al3+] = [Al]T / { cK1 [OH-] + cK2 [SO42-] + cK3 [F-] + cK4 [L-]}
where [OH-] is known from pH and concentration of other ligands
are assumed equal to their known total concentration
Concentrations of ligands other than OH- then calculated, as with
[SO42-] = [SO42-]T / { 1 + cK2 [Al3+]}
Step 1 end
Use revised concentrations of ligands to
improve estimate of [Al3+], beginning Step 2
Continue until convergence reached
Change in estimated concentrations from Stepi to Stepi + 1
< arbitrary criterion
Limitations to predicting speciation
Completeness –may ignore important reactions (redox and speciation)
Insufficient data –do not have conditional stability constants
Analytical methodology –short-comings as in failure to distinguish
between monomeric / polymeric or dissolved / particulate forms
Assumption of equilibrium –ignores kinetics
Field soils –conditions vary from those for which cKis determined;
spatial / temporal variability, particularly mass inputs / outputs
Spreadsheet calculation problem
[Al]T = 0.000010 M
[SO42-]T = 0.000050 M
[F-]T = 0.000002
[L-]T = 0.000010
pH = 4.60
cK
1
cK
2
cK
3
cK
4
= 109.00 M-1
= 103.20
= 107.00
= 108.60
Solve for all forms
See spreadsheet.
Also, do problem 6.
The distribution coefficients, αis, = [H2CO3] / [CO3T], etc., where
[CO3T] = [H2CO3] + [HCO3-] + [CO32-]
Using the given CKSs,
[HCO3-] = CK2 [H+] [CO3-2]
but
[CO32-] = [H2CO3] / (CK1 [H+]2)
so
[HCO3-] = (CK2 / CK1) ([H2CO3] / [H+])
and substituting in [1] gives
[CO3T] = [H2CO3] {1 + (CK2 / CK1) / [H+] + 1 / (CK1 [H+]2)}
and using [H+] = 10-pH the distribution coefficient for H2CO3 is
αH2CO3 = 1 / {1 + 10-6.4 10pH + 10-16.7 102pH}
[1]
Proceeding similarly,
αHCO3 = 1 / {106.4 10-pH + 1 + 10-10.3 10pH}
αCO3 = 1 / {10-16.7 10-2pH + 1010.3 10-pH +1}
Now, when is HCO3- dominant, i.e., αHCO3 ≥ 0.5?
This is the case when {106.4 10-pH + 1 + 10-10.3 10pH} ≤ 2, no?
This is almost the case when either pH = 6.4 or pH = 10.3 because
at either pH, {106.4 10-pH + 1 + 10-10.3 10pH} is only slightly greater than 2, e.g.,
{106.4 10-6.4 + 1 + 10-10.3 106.4} = 1 + 1 + 0.00013 = 2.00013
Thus, HCO3 is (approximately) dominant at 6.4 ≤ pH ≤ 10.3
The earlier [Al3+] speciation problem can be handled more efficiently.
Express the concentrations of ligands in terms of [Al3+] and total
concentration of each ligand to give,
[Al3+] = [Al]T / { (cK1 KW / [H+]) + (cK2 [SO42-]T / {1 + cK2 [Al3+]}) +
(cK3 [F-]T / {1 + cK3 [Al3+]}) + (cK4 [L-]T / {1 + cK4 [Al3+]})}
and approximate a solution for [Al3+] (below). In turn, the equilibrium
concentrations of all species are known from the relations,
[SO42-] = [SO42-]T / {1 + cK2 [Al3+]}, etc.
Of course, there remains the problem that the various cKis may be unknown.
This can be handled if the thermodynamic stability constants are known.
Note on Newton-Raphson Method
[Al3+] = [Al]T / { (cK1 KW / [H+]) + (cK2 [SO42-]T / {1 + cK2 [Al3+]}) +
(cK3 [F-]T / {1 + cK3 [Al3+]}) + (cK4 [L-]T / {1 + cK4 [Al3+]})}
can be quickly approximated using this technique.
As an example, solve the cubic, T = a1X +a2X2 + a3X3. First, write F(X) as
F = a1X + a2X2 + a3X3 – T
If guessed a value of X that gives F = 0, then T = a1X + a2X2 + a3X3 and no need
to go further, but likely F  0. In this case, differentiate F(X) to give,
dF / dX = a1 + 2a2X + 3a3X2
If the slope is evaluated at the initial guess, X1, an estimated solution, X2, is
calculated from the definition of slope as rise / run, i.e.,
(0 – F1) / (X2 – X1) = dF / dX
Repeat steps to estimate an arbitrarily accurate solution. Next figure illustrates.
0.4
guess
0.3
0.2
second
calculated X
F(X)
0.1
0.0
-0.1
-0.2
calculated X
based on guess
-0.3
-0.4
0.0
0.2
0.4
0.6
X
0.8
1.0
Thermodynamic Stability Constant
Activities instead of concentrations
[MgSO4] / [Mg2+][SO42-] = cKs
(MgSO4) / (Mg2+)(SO42-) = Ks
but activity coefficients, i, convert from cKs to Ks, as with
2+ [Mg2+] = (Mg2+)
So that if the ionic strength of the solution is known, the activity
coefficients can be calculated and the appropriate conditional
stability constant calculated as for this example,
cK
s
= (2+ 2+ / 0) Ks
Debye-Hückel
Notes on Chemical Potential
Recall
ΔG = ΔGo + RT ln K
Chemical potential of i, μi, = (∂G / ∂ni)T,P , is related to activity of i, ai, by
μi = μio + RT ln ai
For the reaction aA + bB = cC + dD,
(cμC + dμD – aμA – bμB) = (cμCo + dμDo – aμAo – bμBo) + RT ln (aAaaBb / aCcaDd)
So, ΔG = (cμC + dμD – aμA – bμB) and ΔGo = (cμCo + dμDo – aμAo – bμBo).
At equilibrium,
ΔG = Σviμi, that is, using the above reaction,
cμC + dμD = aμA + bμB
Development of Ion Activity Coefficient
Write chemical potential in terms of concentration and activity coefficient, a = γm,
and consider deviation from ideal behavior (γ < 1) is due to electrostatic interactions
among ions, i.e.,
μ = μEL + μ* = RT ln γ + RT ln m,
i.e.,
μEL = RT ln γ
The idea is to relate μEL = RT ln γ to electric potential, φ*, in the vicinity of an ion.
Take the single, central ion as a point charge for which the radial electric potential is
(1 / r2) d (r2 (dφ / dr)) / dr = - 4πρ / D
[2A]
where ρ is charge density and D is dielectric constant.
[2A], Poisson’s equation, arises in classical electromagnetic theory from relationships
among charge density, electric field and electric potential. The electric field is given
by the (-) potential gradient and the gradient of the electric field on the surface of
a volume containing charge depends directly on the charge contained. So, charge
can be expressed in terms of the (-) second derivative of potential. In this case,
the equation is one-dimensional (radially symmetric).
To solve [2A] ρ must be expressed in terms of potential, φ.
Since ρ = Σzieni, where zi is valance, e is single electronic charge and ni is concentration, ni can be related to potential by
ni = nioexp(-zieφ /kT)
[2B]
where nio is average, bulk concentration (ions per mL) , k is the Boltzmann constant
(R / NA) and T is absolute temperature.
[2B] arises in statistical mechanics, so it is probabilistic. The notion is for a given
total amount of energy in a system, the bodies (molecules, etc. ) that comprise the
system are distributed among the essentially infinite number of energy microstates
possible, but more commonly exist in lower energy states (-zieφ being energy).
The exponential arises from a logrithmic approximation for factorials (probability
calculations), and the denominator, kT (= RT / NA), comes from thermodynamic
calculations.
(1 / r2) d (r2 (dφ / dr)) / dr = -(4π / D) Σzienioexp(-zieφ /kT)
If the exponential is expressed as a series and truncated at the first two terms,
1 – zieφ / kT,
(1 / r2) d (r2 (dφ / dr)) / dr = -(4π / D) Σzienio + (4π / D) Σzi2e2nioφ / kT
Electrical neutrality results in the first term on the right hand side being zero, leaving
(1 / r2) d (r2 (dφ / dr)) / dr = (4π / D) Σzi2e2nioφ / kT
for which (4π / D) Σzi2e2nioφ / kT is written as κ2φ, i.e., κ2 = (4π / D) Σzi2e2nio / kT
(1 / r2) d (r2 (dφ / dr)) / dr = κ2φ
The final matter is to relate potential, φ* = - (zieκ / D), to chemical potential,
μEL (= RT ln γ).
The approach taken is to charge a mole of central ions, each within the potential
of its ion atmosphere, from zero to its actual charge,
μEL = NA  φ* d(zie) = NA -(zieκ / D) d(zie) = -NA zi2e2κ / 2D
If κ = [(4π / D) Σzi2e2nio / kT]1/2 is substituted,
μEL = -NA zi2e2 [(4π / D) Σzi2e2nio / kT]1/2 / 2D
and from μEL = RT ln γ
log γi = -NA zi2e2 [(4π / D) Σzi2e2nio / kT]1/2 / (2.303 2DRT)
Since the concentrations, nio, are in ions per mL and the final form of this model
for a single ion activity coefficient is written in terms of ionic strength
(I = ½ Σzi2mi, m is moles / kg),
log γi = - zi2 [NA2e3 / (2.303 (DRT)3/2)][2πρ /1000]1/2 I1/2
where ρ is solution density. For water at 25 oC, the two bracketed factors
multiply to 0.511, and
log γi = -0.511 zi2 I1/2
Debye-Hückel limiting –applicable for I < 0.01
If consider ion is not a point charge, the earlier constant A (= zie / D) is
expressed as,
A = zie / D [ exp (κa) / (1 + κa)]
where a is the minimum distance of approach.
This leads to an expression for the potential due to the ion atmosphere
about the central ion
φ* = - zieκ / (D [1 + κa])
Integrating to find μEL, relating μEL to the activity coefficient (μEL = RT ln γ)
and solving for γ gives
log γ = -A Zi2 {I0.5 / [ 1 + BaiI0.5 ]}
Applicable for I < 0.1
Models for ionic activity coefficients based on ionic strength, I
where I = 0.5  Zk2 [m]
Debye-Huckel Limiting
Log i = -0.511 zi2 I1/2
Debye-Huckel
log i = -A Zi2 {I0.5 / [ 1 + BaiI0.5 ]}
Davies
log i = -A Zi2 ( {I0.5 / [ 1 + I0.5]} – 0.3 I)
where A = 0.512
Semiempirical models for uncharged species are
log ML = -0.192 I / [ 0.0164 + I], for monvalent cations (M = Na+ etc.)
log ML = -0.300 I, for divalent cations (M = Ca2+ etc.)
log HL = 0.100 I, for proton complexes
A useful empirical relationship for soils is the Marion-Babcock model
which relates ionic strength to electrical conductivity
log I = 1.159 + 1.009 log 
where  is electrical conductivity in dS m-1
Do problem 15 (next slide).
Problems 4, 7 and 13
The equilibrium expressions in terms of CKS and KS are related by
KS = (AlSO4+) / (Al3+)(SO42-) = CKS + / 3+ 2-
Thus, CKS / KS = 3+ 2- / +
So since I increases with electrical conductivity, , through Marion-Babcock,
whether CKS increases or decreases with increasing I, depends on the
relative effect of increasing I on the ratio, 3+ 2- / +.
Using the Debye-Hückel limiting, log γi = -0.511 zi2 I1/2, to illustrate,
3+ 2- / + = 10-0.511 (9 + 4 - 1) I½ = 10-6.132 I½