Download Potential - Chabot College

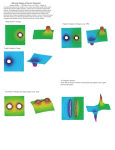
Chapter 23
Electric Potential
PowerPoint® Lectures for
University Physics, Thirteenth Edition
– Hugh D. Young and Roger A. Freedman
Lectures by Wayne Anderson
Copyright © 2012 Pearson Education Inc.modified Scott Hildreth Chabot College 2016
Goals for Chapter 23
• To calculate electric potential energy of a
group of charges
• To understand electric potential
• To calculate electric potential due to a
collection of charges
• To use equipotential surfaces to understand
electric potential
• To calculate E field using electric potential
Introduction
• How is electric potential related to
welding?|
• What is the difference between
electric potential and electric
potential energy?
• How is electric potential energy
related to charge & electric fields?
Electric potential energy in a uniform field
• Behavior of point charge in uniform electric field is
analogous to motion of a baseball in a uniform
gravitational field.
Electric potential energy in a uniform field
• Behavior of point charge in uniform electric field is
analogous to the motion of a baseball in a uniform
gravitational field.
g
Ball
speeds
up
Electric potential energy in a uniform field
• Behavior of point charge in uniform electric field is
analogous to the motion of a baseball in a uniform
gravitational field.
E
+
charge
speeds
up
A positive charge moving in a uniform field
• If positive charge moves in direction of field, KE
increases & potential energy decreases
A positive charge moving in a uniform field
• If +positive charge moves in direction of field,
potential energy decreases (KE increases!)
• If +positive charge moves opposite field,
potential energy increases.
Q23.1
When a positive charge moves in the
direction of the electric field,
A. the field does positive work on it
and the potential energy increases.
B. the field does positive work on it
and the potential energy decreases.
C. the field does negative work on it
and the potential energy increases.
D. the field does negative work on it
and the potential energy decreases.
E
+q
Motion
E
A23.1
When a positive charge moves in the
direction of the electric field,
A. the field does positive work on it and
the potential energy increases.
B. the field does positive work on it
and the potential energy decreases.
C. the field does negative work on it
and the potential energy increases.
D. the field does negative work on it
and the potential energy decreases.
E
+q
Motion
E
A negative charge moving in a uniform field
• Positive charge movement in an E field is like normal
mass moving in a uniform gravitational field.
– Move with the field direction, KE increases
– Move against the field direction, U increases
– Overall, total energy U + KE is constant.
• With negative charges, just reverse the sign! 
A negative charge moving in a uniform field
• If negative charge moves in direction of E field,
potential energy increases…
A negative charge moving in a uniform field
• If negative charge moves in direction of field,
potential energy increases, but if - charge moves
opposite field, potential energy decreases.
Q23.3
When a negative charge moves in the
direction of the electric field,
A. the field does positive work on it
and the potential energy increases.
B. the field does positive work on it
and the potential energy decreases.
C. the field does negative work on it
and the potential energy increases.
D. the field does negative work on it
and the potential energy decreases.
© 2012 Pearson Education, Inc.
E
–q
Motion
E
A23.3
When a negative charge moves in the
direction of the electric field,
A. the field does positive work on it and
the potential energy increases.
B. the field does positive work on it and
the potential energy decreases.
C. the field does negative work on it
and the potential energy increases.
D. the field does negative work on it
and the potential energy decreases.
© 2012 Pearson Education, Inc.
E
–q
Motion
E
A negative charge moving in a uniform field
• Positive charge movement in an E field:
–
Move with the field direction, KE increases
– Move against the field direction, U increases
– Overall, total energy U + KE is constant.
• Negative charges movement in an E field:
–
Move with the field direction, KE decreases
– Move against the field direction, U decreases
– Overall, total energy U + KE is constant.
Q23.2
When a positive charge moves opposite
to the direction of the electric field,
A. the field does positive work on it
and the potential energy increases.
B. the field does positive work on it
and the potential energy decreases.
C. the field does negative work on it
and the potential energy increases.
D. the field does negative work on it
and the potential energy decreases.
© 2012 Pearson Education, Inc.
E
Motion
+q
E
A23.2
When a positive charge moves opposite
to the direction of the electric field,
A. the field does positive work on it
and the potential energy increases.
B. the field does positive work on it
and the potential energy decreases.
C. the field does negative work on it
and the potential energy increases.
D. the field does negative work on it
and the potential energy decreases.
© 2012 Pearson Education, Inc.
E
Motion
+q
E
Q23.4
When a negative charge moves opposite
to the direction of the electric field,
A. the field does positive work on it
and the potential energy increases.
B. the field does positive work on it
and the potential energy decreases.
C. the field does negative work on it
and the potential energy increases.
D. the field does negative work on it
and the potential energy decreases.
© 2012 Pearson Education, Inc.
E
Motion
–q
E
A23.4
When a negative charge moves opposite
to the direction of the electric field,
A. the field does positive work on it
and the potential energy increases.
B. the field does positive work on it
and the potential energy decreases.
C. the field does negative work on it
and the potential energy increases.
D. the field does negative work on it
and the potential energy decreases.
© 2012 Pearson Education, Inc.
E
Motion
–q
E
Electric potential energy of two point charges
• What is the change in electric
potential energy of charge q0 moving
along a radial line?
b
a
+ q (fixed)
Test charge q0
moves from a to b
in the field created
by q
Electric potential energy of two point charges
•
The electric potential energy of
charge q0 moving along a radial
line
qq0
Fr 
40 r 2
1
•
b
Wab
NOTE!! This force is NOT
constant! It decreases with
distance away from +q !
You HAVE to integrate!
b
qq0 1 1
1 qq0
  Fr dr  
dr 
(  )
2
40 r
40 ra rb
a
a
Electric potential energy of two point charges
•
The electric potential energy of
charge q0 moving along a radial
line
qq0
Fr 
40 r 2
1
•
b
Wab
NOTE!! This force is NOT
constant! It decreases with
distance away from +q !
You HAVE to integrate!
b
qq0 1 1
1 qq0
  Fr dr  
dr 
(  )
2
40 r
40 ra rb
a
a
Electric potential energy of two point charges
•
The electric potential energy of
charge q0 moving along a radial
line
b
Wab
b
qq0 1 1
1 qq0
  Fr dr  
dr 
(  )
2
40 r
40 ra rb
a
a
Graphs of the potential energy
• Electrical Potential Energy
1 qq0
U
40 r
• Define U = 0 @ r = ∞
• Sign depends on charges
Gravity is a “conservative” force…
• Change in gravitational potential
energy is same whether mass
moves along an arbitrary path!
dl
mg
b
Wa b   F cos   dl
a
b
  mg cos   dl
a
Electricity is a “conservative” force…
• Electric potential is same whether q0
moves along an arbitrary path!
b
Wa b   F cos   dl
a
b
qq0

cos   dl
2
40 r
a
1
qq0 1 1

(  )
40 ra rb
Electric potential energy of two point charges
•
Electric potential is same whether
q0 moves along an arbitrary path!
b
Wa b   F cos   dl
a
b
qq0

cos   dl
2
40 r
a
1
qq0 1 1

(  )
40 ra rb
Example 23.1 – Conservation of Energy
• Positron (+ electron) moves near alpha particle
(+2e with mass m=6.64 x 10-27 kg)
• Interacts electrically; at r = 1.00 x 10-10 m
moving away at v = 3.00 x 106 m/s.
• What is positron speed when twice as far? At ∞ ?
• Assume a particle doesn’t move.
Example 23.1 – Conservation of Energy
• Positron moves near alpha particle (m=6.64 x 10-27 kg)
• Interacts electrically; at r = 1.00 x 10-10 m moving away at
v = 3.00 x 106 m/s.
• What is positron speed when twice as far? At ∞ ?
• Assume a particle doesn’t move.
• With no external forces doing work, energy is
conserved!
Kb  U b  K a  U a
1
1
2
31
6
2
K a  mva  (9.11x10 kg)(3.00 x10 m / s )
2
2
K a  4.10 x10 18 J
Example 23.1 – Conservation of Energy
• Positron moves near alpha particle (m=6.64 x 10-27 kg)
• Interacts electrically; at r = 1.00 x 10-10 m moving away at
v = 3.00 x 106 m/s.
• What is positron speed when twice as far? At ∞ ?
• Assume a particle doesn’t move.
qq0
Ua 
 (9 x109 Nm 2 / C 2 )(3.2 x10 19 C )(1.6 x10 19 C )
40 r
1
 4.61x10 18 J
Example 23.1 – Conservation of Energy
• Positron moves near alpha particle (m=6.64 x 10-27 kg)
• Interacts electrically; at r = 1.00 x 10-10 m moving away at
v = 3.00 x 106 m/s.
• What is positron speed when twice as far? At ∞ ?
• Assume a particle doesn’t move.
qq0
Ua 
 (9 x109 Nm 2 / C 2 )(3.2 x10 19 C )(1.6 x10 19 C )
40 r
1
 4.61x10 18 J
Problem 23. 1
A point charge with a charge q1 = 3.90μC is held
stationary at the origin. A second point charge with a
charge q2 = -4.80μC moves from the point
x= 0.170m , y=0
to the point
x= 0.230m , y= 0.270m .
How much work is done by Electric Force
from q1 on q2?
Electrical potential with several point charges
• Electrical PE associated with q0
depends on other charges and
distances from q0
• Key example 23.2:
•
Two point charges on x axis
•
q1 = -e at x = 0
•
q2 = +e at x = a
•
Work done to bring q3 = +e
from ∞ to x = 2a?
Q23.5
The electric potential energy of two
point charges approaches zero as the
two point charges move farther away
from each other.
If the three point charges shown here
lie at the vertices of an equilateral
triangle, the electric potential energy
of the system of three charges is
Charge #2
+q
Charge #1
+q
y
A. positive.
B. negative.
C. zero.
D. not enough information given to decide
© 2012 Pearson Education, Inc.
x
–q
Charge #3
A23.5
The electric potential energy of two
point charges approaches zero as the
two point charges move farther away
from each other.
If the three point charges shown here
lie at the vertices of an equilateral
triangle, the electric potential energy
of the system of three charges is
Charge #2
+q
Charge #1
+q
y
A. positive.
B. negative.
C. zero.
D. not enough information given to decide
© 2012 Pearson Education, Inc.
x
–q
Charge #3
Q23.6
The electric potential energy of two
point charges approaches zero as the
two point charges move farther away
from each other.
If the three point charges shown here
lie at the vertices of an equilateral
triangle, the electric potential energy
of the system of three charges is
Charge #2
–q
Charge #1
+q
y
x
A. positive.
B. negative.
C. zero.
D. not enough information given to decide
© 2012 Pearson Education, Inc.
–q
Charge #3
A23.6
The electric potential energy of two
point charges approaches zero as the
two point charges move farther away
from each other.
If the three point charges shown here
lie at the vertices of an equilateral
triangle, the electric potential energy
of the system of three charges is
Charge #2
–q
Charge #1
+q
y
x
A. positive.
B. negative.
C. zero.
D. not enough information given to decide
© 2012 Pearson Education, Inc.
–q
Charge #3
Q23.7
The electric potential due to a point
charge approaches zero as you move
farther away from the charge.
If the three point charges shown here
lie at the vertices of an equilateral
triangle, the electric potential at the
center of the triangle is
Charge #2
+q
Charge #1
+q
y
x
A. positive.
B. negative.
C. zero.
D. not enough information given to decide
© 2012 Pearson Education, Inc.
–q
Charge #3
A23.7
The electric potential due to a point
charge approaches zero as you move
farther away from the charge.
If the three point charges shown here
lie at the vertices of an equilateral
triangle, the electric potential at the
center of the triangle is
Charge #2
+q
Charge #1
+q
y
x
A. positive.
B. negative.
C. zero.
D. not enough information given to decide
© 2012 Pearson Education, Inc.
–q
Charge #3
Q23.8
The electric potential due to a point
charge approaches zero as you move
farther away from the charge.
If the three point charges shown here
lie at the vertices of an equilateral
triangle, the electric potential at the
center of the triangle is
Charge #2
–q
Charge #1
+q
y
x
A. positive.
B. negative.
C. zero.
D. not enough information given to decide
© 2012 Pearson Education, Inc.
–q
Charge #3
A23.8
The electric potential due to a point
charge approaches zero as you move
farther away from the charge.
If the three point charges shown here
lie at the vertices of an equilateral
triangle, the electric potential at the
center of the triangle is
Charge #2
–q
Charge #1
+q
y
x
A. positive.
B. negative.
C. zero.
D. not enough information given to decide
© 2012 Pearson Education, Inc.
–q
Charge #3
Problem 23. 8
Three equal 1.70-μC point charges are
placed at the corners of an equilateral
triangle whose sides are 0.600m long.
What is the potential energy of the system?
(Take as zero the potential energy of the
three charges when they are infinitely far
apart.)
© 2012 Pearson Education, Inc.
Electric potential
• Potential is potential energy per unit charge.
• Think of potential difference between points a and b in an
electric field in either of two ways.
a
b
Electric potential
• Potential is potential energy per unit charge.
• One Way: Potential of a with respect to b
(Vab = Va – Vb)
 work done by the electric force on a unit charge that moves
from a to b in the field.
 if b is at a lower potential than a, work done
moving + charge is positive (it speeds up!)
Electric potential
• Potential is potential energy per unit charge.
• Potential of a with respect to b (Vab = Va – Vb) equals:
 work done by the electric force on a positive unit charge that
moves from a to b in the field.
 Think of gravity doing positive work on a falling mass
Note limits of integration, and their order!
Electric potential analogy to gravity…
• Fg and dl vectors are in
the same direction
a
dl
g
• Work is positive
• Potential decreases
• Va > Vb
b
Electric potential analogy to gravity…
a
• Fe and dl vectors are in
the same direction
+
dl
E
• Work is positive
• Potential decreases
• Va > Vb
b
Electric potential
• Potential is potential energy per unit charge.
• Another Way: Potential of a with respect to b (Vab = Va – Vb)
 work done by you to move a unit charge slowly the other
way, from b to a against the electric force.
 Think of lifting a mass against gravitational force!
a
Va  Vb   E  dl
b
Electric potential analogy to gravity…
• Fg and dl vectors are in
opposite directions
a
dl
g
• Work is negative
• Potential increases
• Va > Vb
b
Electric potential
• Potential is potential energy per unit charge.
• Think of potential difference between points a and b in either
of two ways. Potential of a with respect to b
(Vab = Va – Vb) equals:
 work done by the electric force when a unit charge moves
from a to b.
 work done by you to move a unit charge slowly
from b to a against the electric force.
a
Va  Vb   E  dl
b
b
  E  dl
a
Potential due to charges
• Potential is a scalar
• Three “standard” forms
U
1 q
V

q0 4 0 r
 potential due to a point charge 
U
1
V

q0 4 0
qi
i r
i
1
dq
V
4 0  r
 potential due to a continuous distribution of charge 
 potential due to a collection of point charge 
Finding electric potential from the electric field
• Move in direction of E field
electric potential decreases,
but if you move opposite the
field, the potential increases.
• For EITHER + or – charge!
Potential due to two point charges
• Example 23.3:
• Proton moves .50 m in a straight line
between a and b.
• E = 1.5x107 V/m from a to b.
• Force on proton?
• Work done by field?
• Va – Vb?
Problem 23. 13
A small particle has charge -5.00μC and
mass 2.00×10−4kg . It moves from point A,
where the electric potential is VA = +200V , to
point B, where the electric potential VB =
+800V is greater than the potential at point A.
The electric force is the only force acting on
the particle. The particle has a speed of
5.00m/s at point A.
What is its speed at point B?
© 2012 Pearson Education, Inc.
Potential due to two point charges
• Example 23.4:
•
Dipole with q1 = +12 nC
& q2 = -12 nC
•
d = 10 cm
•
Va ? Vb ? Vc ?
Potential due to two point charges
• Example 23.4:
•
•
•
•
•
Dipole with q1 = +12 nC
& q2 = -12 nC
•
d = 10 cm
•
Va ? Vb ? Vc ?
Does this make sense???
Potential @a (relative to ) = Va: NEGATIVE
Vb: POSITIVE
Vc: ZERO!
Finding potential by integration
•
Example 23.6: Potential at a
distance r from a point charge?
ba

Va  Vb EEdl
dl
ab
•
Here a = r, b = 
Videos to help?
http://apphysicslectures.com/E_M_Videos.html#unit_K
Finding potential by integration
•
Example 23.6: Potential at a
distance r from a point charge?
b
Va  Vb   E  dl
a
Or equally
a
Va  Vb    E  dl
b
•
Here a = r, b = 
Moving through a potential difference
• Example 23.7 combines electric potential with energy
conservation.
• Dust particle m = 5.0 x 10-9 kg, charge +2.0 nC
• Starts at rest. Moves from a to b. Speed at b?
Moving through a potential difference
• Field is NOT constant!
Forces are NOT constant!!
• Use Energy Conservation instead…
• Ka+Ua= Kb+Ub where U = q0V & V = Skq/r
Calculating electric potential
• Example 23.8
(a charged conducting
sphere).
• Total charge q in
sphere of radius R
• V = ? everywhere
Calculating electric potential
• Example 23.8
(a charged conducting
sphere).
• Total charge q in
sphere of radius R
• Start with E field!
• E outside R looks like
pt charge!
• E inside = 0
(conductor!
Calculating electric potential
• Example 23.8
(a charged conducting
sphere).
• Total charge q in
sphere of radius R
• V = ? Everywhere
• V inside must be?
• NOT zero!
• Just CONSTANT!!
• V outside = point
charge!
Oppositely charged parallel plates
• Example 23.9: Find potential at any height y between 2
oppositely charged plates
Example 23.9: Oppositely charged parallel plates
b
Va  Vb   E  dl
a
Example 23.9: Oppositely charged parallel plates
b
b
a
a
Va  Vb   E  dl  E  dl  Ed
An infinite line charge or conducting cylinder
• Example 23.10 – Potential at
r away from line?
b
Va  Vb   E  dl
a
 
E (r ) 
r
20 r
An infinite line charge or conducting cylinder
• Example 23.10 – Potential at
r away from line?
b
Va  Vb   E  dl
a
 
E (r ) 
r
20 r
b
Va  Vb   E  dl
a
An infinite line charge or conducting cylinder
• Example 23.10 – Potential at
r away from line?
b
Va  Vb   E  dl
a
 
E (r ) 
r
20 r

dr
Va  Vb   E  dl 

20 ra r
a
b
rb
An infinite line charge or conducting cylinder
• Example 23.10 – Potential at
r away from line?
b
Va  Vb   E  dl
a
 
E (r ) 
r
20 r
rb

dr

Va  Vb   E  dl 

ln

20 ra r 20 ra
a
b
rb
An infinite line charge or conducting cylinder
• Example 23.10 – Potential at
r away from line?
rb

Va  Vb 
ln
20 ra
If Vb = 0 at infinite distance, won’t
Va go to infinity at r = 0??
Yes!
So define V= 0 elsewhere
ro

Vr 
ln
20 r
An infinite line charge or conducting cylinder
• Consider cylinder…
• Same result for r > R
• What about inside
conducting cylinder??
A ring of charge
• Charge Q uniformly around thin ring of radius a. VP=?
A finite line of charge
• Example 23.12 – Potential at P a distance x from ring?
Equipotential surfaces and field lines
• Equipotential surface is surface on which electric potential is
same at every point.
• Field lines & equipotential surfaces are always mutually
perpendicular.
Equipotential surfaces and field lines
• Equipotential surface is surface on which electric potential is
same at every point.
• Field lines & equipotential surfaces are always mutually
perpendicular.
Equipotential surfaces and field lines
• Equipotential surface is surface on which electric potential is
same at every point.
• Field lines & equipotential surfaces are always mutually
perpendicular.
Equipotentials and conductors
• When all charges are at rest:
 Surface of conductor is always an equipotential surface.
 E field just outside conductor is always perpendicular to surface
 Entire solid volume of conductor is at same potential.
Potential gradient
• Consider a uniform vector E field
• Consider moving a unit charge along x-axis a very small
distance from x to x+Δx (at constant y and z)
• Work done against field from x to x+Δx:
x  x
Work/unit  
charge
 E  dl   E x
x
x
Work against field by you
Potential gradient
• Consider a uniform vector E field
• Consider moving a unit charge along x-axis a very small
distance from x to x+Δx (at constant y and z) in this field
• YOU have to do work against field from x to x+Δx
• Remember Work by you against field = PE
•
You lift mass up against gravity = gain in grav. PE!
•
You push + charge against E field = gain in elec. PE!
• Your work against the field increases the potential energy.
Potential gradient
• Consider a uniform vector E field
• Consider moving a unit charge along x-axis a small
distance from x to x+Δx (at constant y and z)
• But Work (per unit charge) done against field =  V
Work
 V ( x  x, y, z )  V ( x, y, z )
unit q
Final position
Initial position
Potential gradient
• Consider a uniform vector E field
• Consider moving a unit charge along x-axis a small
distance from x to x+Δx (at constant y and z)
• But Work (per unit charge) done against field =  V!
• In the limit as Δx goes to 0…
W
V
 V ( x  x, y, z )  V ( x, y, z ) 
x
unit q
x
Potential gradient
• So uniform vector E field is the gradient of a scalar Potential
V
Work / unit q   Ex x 
x
x
so
V
Ex  
x
Potential gradient
• Create E as the gradient of the Potential
V
Ex  
x
V
Ey  
y
V
Ez  
z
  
E  ( , , )V  V
x y z
Potential gradient
• Create E as the gradient of the Potential
  
E  ( , , )V  V
x y z
  gradient vector operator
  " grad "
Potential gradient
• Analogy to Gravitational Potential Gradient = direction of
force along steepest slope
Top down
view
Lines of constant height =
constant “gh” =
(Potential Energy/unit mass)
Potential gradient
• Analogy to Gravitational Potential Gradient = direction of
force along steepest slope
Top down
view
Side view
Lines of equal
gravitational
potential
(regardless of
mass)
Potential gradient
• Analogy to Gravitational Potential Gradient = direction of
force along steepest slope
Top down
view
Biggest change in (m)gh for
small distance sideways
(m)gh decreases in y direction quickly
with small movement in x
Potential gradient
• Analogy to Gravitational Potential Gradient = direction of
force along steepest slope
Top down
view
Steepest slope means
largest net force in direction
of gravitational field
Largest negative change in (m)gh with
small change in horizontal direction
Potential gradient
• Analogy to Gravitational Potential Gradient = direction of
force along steepest slope
Top down
view
Steepest slope means
largest net force in direction
of gravitational field
 
F  ( , )U  U
x y
Largest negative change in (m)gh
with small change in xy direction
Potential gradient
• Create E as the gradient of the Potential
3V
4V
Lines of constant
electric potential (Volts)
(Potential Energy/unit
charge)
5V
6V
Potential gradient
• Create E as the gradient of the Potential
3V
4V
Lines of constant
electric potential (Volts)
(Potential Energy/unit
charge)
5V
6V
Largest negative change in Volts with
small change in horizontal direction =
direction of E field!
Potential gradient
• Create E as the gradient of the Potential
  
E  ( , , )V  V
x y z
•
Potential decreases in direction of + E field
•
Va – Vb is positive if E field points from a to b
•
“Grad V” is from final position – initial = Vb – Va <0
•
So
 V
is positive!