* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Lecture 9
Conservation of energy wikipedia , lookup
Elementary particle wikipedia , lookup
History of subatomic physics wikipedia , lookup
Electrostatics wikipedia , lookup
Electric charge wikipedia , lookup
Density of states wikipedia , lookup
Nuclear physics wikipedia , lookup
Neutron detection wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Electrical resistivity and conductivity wikipedia , lookup
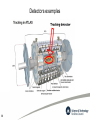
Introduction to Silicon Detectors E.G.Villani STFC Rutherford Appleton Laboratory Particle Physics Department 1 Outlook • Part I : Introduction to physics of Si and detection • Part II: Examples of detectors • Conclusions 2 Introduction The Si detection chain E Sensing/ Charge creation Charge transport and collection Si physical properties Conversion Si device properties Signal processing Data TX Si device topologies properties all the boxes of the detection chain process based upon Silicon 1 Silicon Detector physics: Silicon Physical and Electrical properties Charge Transport Mechanisms Detection principles 3 2 Detector system issues: Conversion - pn junction Detection efficiency Power Microstrips MAPS Detector examples: Silicon properties After Oxygen, Silicon is the 2nd most abundant element in Earth’s crust (>25% in mass) Element of IV group in the periodic table The crystalline structure is diamond cubic (FCC), with lattice spacing of 5.43 A Each atom is surrounded by 4 neighbors Si •Polysilicon consists of small Si crystals randomly oriented; in α-Si there is no long range order. 1.48A 4 Apart from its abundance, the key to success of Si is related to its oxide SiO2, an excellent insulator (BV ~ 107 V/cm). *Micro crystals but the flexible bond angles make SiO2 effectively an amorphous: its conductivity varies considerably (charge transport in SiO2 via polaron hopping between non-bonding oxygen 2p orbitals) Silicon electrical properties Silicon Band structure The electronic band structure can be obtained by solving many-body SE in presence of periodic potential of the crystal lattice: Bloch functions T U E n,k r un,k r e jkr En k ~ a wave associated with free motion of electrons modulated by the periodic solution un,k. The energy E is periodic in k so is specified just within the 1 st unit cell of the reciprocal lattice (the Brillouin zone). 5 VB * The appearance of Energy BAND GAP, separating CB and VB (semiconductor) CB * The 6 CB minima are not located at the center of 1st Brillouin zone, Indirect BAND GAP Silicon electrical properties Ph: DQ~107 m-1 DQ~1010 m-1 p/a The indirect BG of Si requires higher energy for charge excitation, because energy and momentum must be conserved (Phonon-assisted pair creation/recombination) In Si an average of 3.6 eV is required for pair creation 6 Silicon electrical properties The detailed band structure is complicated: usually quasi-equilibrium simplifications are sufficient to study the charge transport. Assuming that the carriers reside near an extremum, the dispersion relationship E(k) is almost parabolic: E k 2 k 2 2m0* 2m g E * 3/ 2 0 2 3 2p E Eo 2 2 k 1 k p E k v E k k 2m0* m0* m0* dk t d p rV F dt dt Under the assumptions of small variation of the electric field, the carrier dynamics resembles that one of a free particle, with appropriate simplifications. The effective mass approximation takes into account the periodic potential of the crystal by introducing an effective carrier mass ( averaged over different longitudinal and transverse masses) . The lower the mass, the higher mobility (µ 1/m*) Similar approach used to calculate the E(k) for phonons. 7 Silicon electrical properties The carrier density is calculated from: • The density of states g(E); • The Fermi distribution function F(E); CB At equilibrium the carrier density in CB and VB is obtained by integrating the product: VB nD g D E F E dE NC /V e EcEv / kT ni pi 3 F E 2 1 2 1 E EF 1 exp kT pn ni N C NV e Eg / kT 10 20 @ T 300 K *Fermi level: energy level @ 50% occupancy 0 In intrinsic Si a creation of e in CB leaves behind a hole in VB, that can be treated as an e with positive charge and mobility of the band where it resides In pure silicon @ room temperature about 1 every 1012 atoms is ionized The density of states gD(E) depends on the dimension 8 Silicon electrical properties Conduction of Si intrinsic @ T = 300K: σ = q(μn +μp) ni = 3.04x10-6mho-cm ->329 kOhm-cm By adding atoms of dopants, which require little energy to ionize( ~10’s mEV, so thermal energies @ ambient temp is enough) we can change by many orders of magnitude the carrier concentration. Doping concentration: 1012 to 1020 cm-3 In crystalline Si ~ 5*1022atoms cm-3 In equilibrium the relationship between carrier concentration and E is the same as in the intrinsic case: pn ni2 N C NV e E g / kT 1020 @ T 300K e.g . : N D 1017 pn pN D p 9 ni2 103 ND Charge transport Charge transport: The charge transport description relies on semi-classical Boltzmann Transport Equation (BTE, continuity equation in 6D phase space) f r , k , t 1 F f r , k , t k E k r f r , k , t k f r , k , t t t n r, t 1 V f r , k , t coll Q conservation q vk f r , k , t V k P conservation 1 E k f r , k , t V k E conservation W r, t S r , k , t k J r, t The distribution function f(r,k) can be approximated near equilibrium: Near equilibrium equilibrium 0 10 k f r , k , t t coll f f0 f Charge transport Under (many) simplifying assumptions the 1st moment of BTE gives the Drift Diffusion model (DD, in many textbooks ‘The semiconductor equations’): J n qn n E r qDnn Drift term Diffusion term J p qp p E r qDp p n 1 Jn Un t q p 1 J p U p t q V p n N D N A Even in low charge injection regime, a small E renders the drift term >> diffusion term DD expresses momentum conservation: it becomes invalid when sharp variation in energy of carriers occur (due to steep electric field gradient as in deep submicron devices) When feature size is 0.’sμm the DD model becomes invalid: higher moments required to express energy conservation (hydrodynamic/Quantum transport/MC…computational electronics) 11 Detection principles When a charged particle penetrates in matter, it will interact with the electrons and nuclei present in the material through the electromagnetic force: the charged particle feels the EM fields of nuclei and electrons and undergoes elastic collisions. If the particle has 1 MeV energy or more, like in nuclear phenomena, the energy is large compared to the binding energy of the electrons in the atom: to first approximation, matter can be seen as a mixture of free electrons and nuclei at rest. Maximum energy transfer in the elastic collision: • collisions with nucleus the particle loses little energy, its momentum can be changed remarkably • collisions with electrons the particle can transfer large energy to electrons (which can have enough energy to travel macroscopic distances) most of the energy loss due to collisions with electrons, most of change of direction due to collisions with nuclei 12 Detection principles Semiconductor detectors are mostly based on Ionization: the detection of electron–hole pairs created in the semiconductor material by ionising radiation. Advantage of semiconductors detectors compared to gas detectors: • The amount of energy needed to produce free pair of charge ( around 1/10th in semiconductors compared to gas) • Higher • High carrier mobility can improve radiation hardness; • Very well developed semiconductor technology implies higher reliability and lower cost; • Can be operated at room temperature; density of semiconductor means higher charge signal; Silicon detectors are commonly used in HEP (i.e. E > 1 GeV) used to localise charged particle trajectories by stacking them onto several layers 13 Detection processes A: Ionization: by imparting energy to break a bond, electrons are lifted from VB to CB then made available to conduction. Most exploited concept ( ionization chambers, microstrip, hybrid pixels, CCD, MAPS…) B: Excitation: Charge or lattice (acoustic or optical phonons) some IR detectors, bolometer CB Quantized levels VB 14 Detection principles Ionization energy loss (/ density) : Bethe formula for charged particles through matter due to interaction with electrons 0.2 < < 1 15 Detection principles Ionization energy loss (/ density) : Bethe formula + corrections Z: charge of particle : density of material : relativistic parameter Ar: relative atomic weight I: mean excitation potential Tmax: max energy transfer : density correction term c: speed of light Losses due to relativistic stretch, bremsstrahlung emissions Bethe formula valid if velocity of particle is larger than orbital electrons velocity Nuclear stopping dominates low energy collisions 16 Detection principles In Silicon a Minimum Ionization Particle releases <390> eV/m the average energy required to produce electrons /holes pairs in Silicon is 3.62 eV Approximately an average of 108 electrons / hole pairs generated in Silicon / m A typical wafer Silicon is 300 m thick -> 32,000 electrons / hole pairs on average generated in a standard thickness size Silicon detector by a MIP 17 Detection principles Whilst the Bethe formula describes the average energy loss of charged particles through matter, one has to consider also the fluctuations of such energy loss by ionization to estimate the most probable value of energy loss. These fluctuations in energy loss in thin (i.e. thin compared to the particle range) detectors, due to delta electrons, are described by a Landau probability density function In a typical 300 μm thick sensor: * 32000 electrons / holes pair generated on average * 21700 electrons / hole generated most probable 18 MPV of energy loss normalized to the mean loss of a MIP Detection principles As the particle penetrates in the medium, its energy loss per unit length will change. The energy loss increases towards the end of the range. Close to the end it reaches a maximum and then abruptly drops to zero. This maximum of the energy loss of charged particles close to the end of their range is referred to in the literature as the ‘Bragg peak’. For example, this is of particular importance for hadron therapy applications, where the aim is to maximise the energy deposited at a specific point within the human body and spare the neighbouring ones. 19 Detection principles Electromagnetic interactions of Charged Particles: Electrons: excitation and ionisation of atoms along the very irregular trajectory. At higher energies, bremsstrahlung loss mechanism becomes important. For energies > 100 keV, electrons will lose about 2 MeV/cm multiplied by the density; Muons: very high energy muons can travel kilometres in matter before losing all energy Positrons: same behaviour of electrons, but after coming to rest, a positron will annihilate with electrons that are always present. This annihilation gives rise to a pair of back-to-back gamma rays of 511 keV. Exploited in PET. Protons: higher ionisation compared to electrons but less than alpha particles. Straight trajectory. The range in solids is of the order of 1 mm. Alpha particles: The energy loss of alpha particles is of the order of 1000 MeV/cm times the density of the medium. Range of only tens of microns in solids and a few centimeters in gases. Straight trajectory. 20 Detection principles Interactions of photons X-rays: photons in the energy range of 1 – 100 keV Gamma rays: photons of energy > 100 keV Photoelectric process: a photon undergoes an interaction with an atom and completely disappears. The energy of the photon is used to increase the energy of one of the electrons in the atom. The electron becomes free or there is Auger emission. Compton scattering: elastic collision between a photon and an electron. Pair production: If the energy of the photon is at least two times larger than the mass of an electron, the energy of the photon can be used to create an electron and positron pair in the nucleus electric field. 21 Detection principles Interactions of photons 10 eV 22 1 keV 1 MeV 1 GeV .1 TeV Detection MIP charge density n Photoelectric charge density dE 1 1 3 1015 cm 3 2 dx i p R R v I 110nm A MIP forms an ionization trail of radius R when traversing Si, creating ~ 100 e-/μm I z I o e E z z n Pin z e 5.6 106 e / m h An optical power of -60dBm (= 1nW) of 1keV photons generates ~ 6*106e-/μm h 1015 cm 2m E L 0.5 1107 cm Low injection regime: The associated wavelength is much smaller than mean free path: Each charge is independent from each other; The dynamics of generated carriers does not require QM The generated charge is too small to affect the internal electric field 23 High injection regime: Plasma effects The internal electric field can be affected by the generated charge Half summary E Sensing/ Charge creation Charge transport and collection Si physical properties Physical characteristics: Quasi equilibrium; Homogeneity; ‘Room’ temperature; Non degenerate Si; Under conditions of • quasi stationary conditions • non degenerate semiconductor • not small feature size • low injection •… 24 Conversion Si device properties Charge transport: Charge generation: Big devices, DD adequate; Ionization: Small injection, QM not needed; Small injection, electric field as static; Stopping power, average ionization energy, fluctuations Outlook • Part I : Introduction to physics of Si and detection • Part II: Examples of detectors • Conclusions Detectors examples The working principle of almost all present-day electronic devices is based on the pn semiconductor junctions. The same principle is the basis of the use of semiconductors as detectors for ionising radiation. Strip / pixel detectors HEP, Scientific applications PN junction Monolithic Active Pixel Sensors (MAPS) Consumer and scientific applications Charge Coupled Devices (CCD) Imaging, scientific and consumer applications 26 Detectors examples Almost all HEP experiments use Si detectors: The high density track region usually covered by pixel detectors; by strip at larger radius (cost reason) 27 Signal conversion: The pn junction Homojunction: two pieces of same semiconductor materials with different doping levels: • In thermal equilibrium, the Fermi level equalizes throughout the structure F • thermal diffusion of charge across the junction leaves a depleted region, with the ionized dopants : an electric potential Φ, and a field F, develops • the charge concentration depends exponentially on Φ: 0 In equilibrium J = 0 0 qnn E r qDnn n n0e D Vt 0 qp p E r qDpp p p0e D Vt • by applying a small voltage to decrease the barrier, the charge increases exponentially • by applying a voltage to increase the barrier, the depleted region Increases Unidirectionality of current characteristics 28 Signal conversion: The pn junction • when charge is generated in the depleted region is swept across by the electric field sustained by the ionized dopants and the biasing. PN junction as signal converter: capacitor with a F across W • A device with a large depleted region can be used to efficiently collect radiation generated charge (Solid state ionization chamber) • the capacitance is a source of noise: lower capacitance (large depleted region) increases the S/N Depletion width W Capacitance 29 C= 2Vb N a N d q Na Nd qe N a × N d ×A 2Vb N a + N d The full depletion voltage is the minimum voltage at which the bulk of the sensor is fully depleted. Signal The operating voltage is usually chosen tojunction be slightly higher conversion: The pn (over depletion). To achieve large W high field region: • Low doping (high resistivity) • Large voltages • typical values: Na= 1015 cm-3,Nd= 1012 W (0V) ≈ 23 μm W(100V) ≈ 360 μm reverse bias voltage V [V] High-resistivity material (i.e. low doping) requires low depletion voltage. Depletion voltage as a function of the material resistivity for two different detector thicknesses (300 µm, 500 µm). resistivity r [kOhm cm] Depletion voltage vs. resistivity ay 2011 30 Thomas Bergauer (HEPHY Vienna) 40 Detectors examples Strip detectors (high res) F ≈ 300μm 80μm Q transversal diffusion Vbias ~100’sV Array of long silicon diodes on a high resistivity silicon substrate A strong F in the high resistivity Si region helps collect charge efficiently. The high resistivity Si is not usually used in mainstream semiconductor industry: Hybrid solution: detector (high resistivity) connected (wire/bump-bonded) to the readout electronic (low resistivity) 31 Detectors examples ATLAS SCT RO ASIC (ABCD3TA) 12 RO ASIC 768 Strip Sensors 128 channels/ASIC RAD-HARD DMILL technology ASICS glued to hybrid 40 MHz Ck ATLAS SCT 4 single-sided p-on-n sensors 2x2 sensors daisy chained Stereo angle 40 mrad Strip pitch 80 um 768 channels/side Binary RO Bias Voltage up to 500 V Operating temperature -2 C Space point resolution: rPhi 17um / z 50 um Power consumption: 5.6 W (initially ) to 10 W ( after 10y) Rad hard upto 2x10^14 1-MeV n eqv/cm2 32 Detectors examples ATLAS SCT 61 m2 of Si 6.3 * 106 channels 50 kW total power consumption 1 barrel - 4 layers - 2100 modules 2 endcaps - 9 disks/each - 988 modules 2 T solenoidal field 33 Detectors examples ATLAS Tracker overview Pixel: (n+ on n) 1.8m2, 80M channels SCT: 6.3M 61 m2 channels TRT: 0.4M channels 34 Detectors examples Barrel insertion in the ATLAS Cavern 35 Detectors examples 36 Detectors in operation 37 Detectors in operation 38 Detectors examples MAPS detectors ≈1’s m RO electronic RO electronic 3T ( 3MOS) MAPS structure 2 D array of pixels Monolithic solution: detector and readout integrated onto the same substrate 39 Detectors examples MAPS detectors Vbias ~V’s N++ (low res) Electronics 0.’s μm Active region P+ (low-med res) ‘s μm P++ (low res) Mechanical substrate 100’s μm The charge generated in the thin active region moves by diffusion mainly: ‘Long’ collection time Small signal Low radiation hardness Complex circuit topologies allow DSP on pixels for low noise 40 Detectors examples Example of MAPS detectors: 10-7 n l2 Dn 2 n U n tcoll t Dn Charge collection time (s) in MAPS vs. perpendicular MIP hit 41 TPAC 1 pixel size 50x50 μm2 Chip size ~1cm2 Total pixels 28k >8Meg Transistors approximately 2000 m2 of Silicon 1012 pixels 10 μW/pixel x 1012 = 107W Assuming Vcc=2V current 6 consumption: 5*10 A Radiation damage In HEP and space applications the detectors are exposed to high level of dose of radiation: LHC: 10’s Mrad (100kGy) over 10years of operation N.B.: 1 rad/cm3 Si ~1013e/h pairs Lethal dose: 500 rad Total Body Irradiation 42 Radiation damage Radiation environment in LHC experiment ATLAS Pixels ATLAS Strips CMS Pixels CMS Strips ALICE Pixel LHCb VELO TID Fluence 50 Mrad 7.9 Mrad ~24Mrad 7.5Mrad 250krad - 1.5 x 1015 2 x 1014 ~6 x 1014 * 1.6 x 1014 3 x 1012 1.3 x 1014/year** All values including safety factors. 43 1MeV n eq. [cm-2] @ 10 years Radiation damage Microscopic effects: Bulk damage to Silicon : Displacement of lattice atoms V EK>25 eV Atoms scattered by incoming particles leave behind vacancies or atoms in interstitial positions (Frenkel pairs). Low energy particle ~ point defects High energy particles ~ cluster defects 44 I Vacancy + Interstitial Radiation damage Energy deposition Atoms displacement altered Lattice periodicity generation recombination Donor levels +++ Band gap Spurious states trapping - Altered Electrical characteristics Conduction band compensation Band gap Acceptor levels Valence band The appearance of spurious band gap states affects the electro/optical characteristics of the device: • Thermal generation of carriers (increased leakage current) • Reduced recombination time ( quicker charge loss , reduced signal) • Charge trapping • Scattering • Type conversion 45 Radiation damage Macroscopic effects: Charge Collection Efficiency (CCE) is reduced by trapping Noise increases because of increase leakage current Depletion voltage increases because of type inversion Qe ,h (t ) Q0 e,h exp 1 eff e ,h t 1015 1MeV n-eq. 1 eff e,h 46 N defects Radiation damage To increase the Radiation Hardness of Sensors: • Operating conditions (cooler – lower leakage) • Material engineering ( OFZ - Diamond detectors) • Device engineering (n in n/p – 3D detectors) • Electrodes in the bulk – lateral collection reduces the drift distance • Lower depletion voltage – less power consumption • difficult to manufacture •3D DDTC similar to 3D but easier to manufacture; also Better mechanical strength. n+ F 47 p+ Conclusions The field of semiconductor detectors encompasses different fields: solid state physics, nuclear and particle physics, electrical engineering, … Some of the issues relevant to modern radiation semiconductor detectors: • Development of new detection techniques based on novel and well established semiconductor material: ( phonon-based detectors, quantum detectors, compounds, low dimensional) • Integration with electronics (monolithic solution to achieve more compactness and reduce cost) 3D structures • Topologies optimization (power reduction is crucial for future large HEP experiments) • Radiation hardness 48