Download week 5 part 1

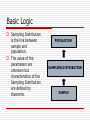
Chapter 7
Estimation Procedures
Basic Logic
 In estimation procedures, statistics
calculated from random samples are
used to estimate the value of
population parameters.
 Example:
 If we know 42% of a random sample
drawn from a city are Conservatives, we
can estimate the percentage of all city
residents who are Conservatives.
Basic Logic
 Information from
samples is used to
estimate
information about
the population.
 Statistics are used
to estimate
parameters.
POPULATION
SAMPLE
PARAMETER
STATISTIC
Basic Logic
 Sampling Distribution
is the link between
sample and
population.
 The value of the
parameters are
unknown but
characteristics of the
Sampling Distribution
are defined by
theorems.
POPULATION
SAMPLING DISTRIBUTION
SAMPLE
Two Estimation Procedures
 A point estimate is a sample statistic used
to estimate a population value.
 A newspaper story reports that 74% of a sample
of randomly selected British Conservative voters
support David Cameron as the new
Conservative party leader
 Confidence intervals consist of a range of
values.
 ”between 71% and 77% of British Conservative
voters approve of David Cameron as leader .”
Constructing Confidence
Intervals For Means
 Set the alpha (probability that the interval
will be wrong).
 Setting alpha equal to 0.05, a 95% confidence
level, means the researcher is willing to be
wrong 5% of the time.
 Find the Z score associated with alpha.
 If alpha is equal to 0.05, we would place half
(0.025) of this probability in the lower tail and
half in the upper tail of the distribution.
 Substitute values into formula 7.1.
Confidence Intervals For Means
 For a random sample of 178
households, average TV viewing was
6 hours/day with s = 3. Alpha = .05.
 See formula 7.2




c.i.
c.i.
c.i.
c.i.
=
=
=
=
6.0
6.0
6.0
6.0
±1.96(3/√177)
±1.96(3/13.30)
±1.96(.23)
± .44
Confidence Intervals For Means
 We can estimate that households in this
community average 6.0±.44 hours of TV
watching each day.
 Another way to state the interval:
 5.56≤μ≤6.44
 We estimate that the population mean is greater
than or equal to 5.56 and less than or equal to
6.44.
 This interval has a .05 chance of being wrong.
 So: With a probability of 95%, we can state
that the households in this community watch
on average between 5.56 and 6.44 hours of TV
each day
Confidence Intervals For Means
 Even if the statistic is as much as
±1.96 standard deviations from the
mean of the sampling distribution the
confidence interval will still include
the value of μ.
 Only rarely (5 times out of 100) will
the interval not include μ.
Constructing Confidence Intervals
For Proportions
 Procedures:
 Set alpha.
 Find the associated Z score.
 Substitute the sample information into
Formula 7.3.
See Healey’s book for more information