Download E - Read

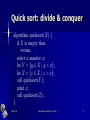
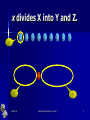
隨機演算法
Randomized Algorithms
呂學一 (Hsueh-I Lu)
http://www.iis.sinica.edu.tw/~hil/
2004/2/25
Randomized Algorithms, Lecture 1
1
Today


Randomized quick sort
Randomized maximum cut
2004/2/25
Randomized Algorithms, Lecture 1
2
Sorting


Input: n distinct numbers x1, x2, …, xn .
Output: a sorted list of x1, x2, …, xn .
4
2004/2/25
3
5
8
1
9
2
Randomized Algorithms, Lecture 1
6
7
3
Quick sort: divide & conquer
algorithm quicksort(X) f
if X is empty then
return;
select a number x;
let Y = fy 2 X j y < xg;
let Z = fz 2 X j z > xg;
call quicksort(Y );
print x;
call quicksort(Z);
g
2004/2/25
Randomized Algorithms, Lecture 1
4
x divides X into Y and Z.
4
2
7
8
1
9
3
6
5
x
4
Y
2004/2/25
Z
Randomized Algorithms, Lecture 1
5
The whole process
4
2
7
8
1
9
3
6
5
2
1
3
4
7
8
9
6
5
1
2
3
6
5
7
8
9
3
5
6
8
9
1
5
2004/2/25
Randomized Algorithms, Lecture 1
9
6
Efficiency depends on …
algorithm quicksort(X) f
if X is empty then
return;
select a number x;
let Y = fy 2 X j y < xg;
let Z = fz 2 X j z > xg;
call quicksort(Y );
print x;
call quicksort(Z);
g
2004/2/25
Randomized Algorithms, Lecture 1
Critical step
7
A bad case
9
8
7
6
5
4
3
2
1
8
7
6
5
4
3
2
1
9
7
6
5
4
3
2
1
8
6
5
4
3
2
1
7
5
4
3
2
1
6
4
3
2
1
5
3
2
1
4
2
1
3
1
2
(n)
1
2004/2/25
Randomized Algorithms, Lecture 1
8
A good case


Each x divides X evenly into Y and Z, i.e.,
when –1· |Y| – |Z| · 1.
The running time is O(n log n).
O(log n)
2004/2/25
Randomized Algorithms, Lecture 1
9
Median selection
F Input: a (multiple) set X of n numbers.
F Output: a number x in X with
¡1 · jfy 2 X j y < xgj ¡ jfz 2 X j z > xgj · 1.

If the median-selection problem can be
solved in O(n) time, then algorithm
quicksort runs in O(n log n) time.
2004/2/25
Randomized Algorithms, Lecture 1
10
How hard is median
selection?

[Blum et al. STOC’72 & JCSS’73]
– A “shining” paper by five authors:
Manuel Blum (Turing Award 1995)
 Robert W. Floyd (Turing Award 1978)
 Vaughan R. Pratt
 Ronald L. Rivest (Turing Award 2002)
 Robert E. Tarjan (Turing Award 1986)

– The number of comparisons required to find a
median is between 1.5n and 5.43n.
2004/2/25
Randomized Algorithms, Lecture 1
11
Number of comparisonss

Upper bound:
– 3n + o(n) by Schonhage, Paterson, and
Pippenger (JCSS 1975).
– 2.95n by Dor and Zwick (SODA 1995, SIAM
Journal on Computing 1999).

Lower bound:
– 2n+o(n) by Bent and John (STOC 1985)
– (2+2-80)n by Dor and Zwick (FOCS 1996,
SIAM Journal on Discrete Math 2001).
2004/2/25
Randomized Algorithms, Lecture 1
12
Question:
Perhaps not!
Do we really need all the
complication of median selection to
obtain an O(n log n)-time quicksort?
2004/2/25
Randomized Algorithms, Lecture 1
13
For example, x does not
have to be a median.
As long as
jY j
jZ j
= £(1), the resulting quicksort runs in O(n log n) time.
O(log n)
2004/2/25
Randomized Algorithms, Lecture 1
14
How many good choices for x?
Observation For example, if we only aim for
jY j
1
·
· 3;
jZj
3
then at least half of the elements x in X are good.
2004/2/25
Randomized Algorithms, Lecture 1
15
This leads to RandQS
隨機快排法
2004/2/25
Randomized Algorithms, Lecture 1
16
Randomized quicksort
algorithm RandQS(X) f
if X is empty then
randomization
return;
select x uniformly at random from X;
let Y = fy 2 X j y < xg;
let Z = fz 2 X j z > xg;
call RandQS(Y );
print x;
call RandQS(Z);
g
2004/2/25
Randomized Algorithms, Lecture 1
17
2 Questions for RandQS
Is RandQS correct?

–
That is, does RandQS “always” output a
sorted list of X?
What is the time complexity of RandQS?

–
–
2004/2/25
Due to the randomization for selecting x, the
running time for RandQS becomes a
random variable.
We are interested in the expected time
complexity for RandQS.
Randomized Algorithms, Lecture 1
18
Features for many
randomized algorithms

Implementation is relatively simple,
– compared to their deterministic counterparts.

The challenge for designing randomized
algorithms are usually in (asymptotic)
analysis for (time and space) complexity.
2004/2/25
Randomized Algorithms, Lecture 1
19
Let C = #comparision.



When we choose x uniformly at random from X,
the probability for each element of X being
chosen as x is exactly 1/|X|.
The values of C for two independent executions
of RandQS are very likely to be different.
So, C is a random variable. We are interested in
determining E[C], since the expected running
time is clearly O(E[C]).
2004/2/25
Randomized Algorithms, Lecture 1
20
Computing E[C] from E[Ci;j ]
Suppose X consists of x1 ; : : : ; xn with x1 < ¢ ¢ ¢ < xn .
Let Ci;j denote the number of times that xi and xj
are compared during the execution of RandQS. By
the linearity of E[¢], we have
2
3
X
X
n
4
5
E[C] = E
Ci;j
i=1 j>i
=
X
X
n
E[Ci;j ]:
i=1 j>i
2004/2/25
Randomized Algorithms, Lecture 1
21
Ci;j can only be 0 or 1.
4
2
7
8
1
9
3
6
5
2
1
3
4
7
8
9
6
5
1
2
3
6
5
7
8
9
3
5
6
8
9
1
5
2004/2/25
Randomized Algorithms, Lecture 1
9
22
Therefore,
E[Ci;j ]
=
=
Pr[Ci;j = 1] ¢ 1 + Pr[Ci;j = 0] ¢ 0
Pr[Ci;j = 1]:
Q: What is the value of Pr[Ci;j = 1]?
Do you think Pr[Ci;j = 1] has a ¯xed value in di®erent executions of RandQS(X)?
2004/2/25
Randomized Algorithms, Lecture 1
23
CLAIM
Pr[Ci;j
2
= 1] =
:
j¡i+1
For example,
Pr[C1;n
2
2
= 1] =
= :
n¡1+1
n
Reason: x1 and xn are compared (once) if and
only if the ¯rst choice of x is either x1 or xn .
2004/2/25
Randomized Algorithms, Lecture 1
24
Another example
For example,
Pr[C2;n
2
2
= 1] =
=
:
n¡2+1
n¡1
?
Yes: x1 and xn are compared (once) if and only if (a) the
¯rst choice of x is either x2 or xn , or (b) the ¯rst choice
of x is x1 and the second choice of x is either x2 or xn .
Therefore,
Pr[C2;n
2
1
2
2
= 1] = + £
=
:
n n n¡1
n¡1
Wow!
2004/2/25
Randomized Algorithms, Lecture 1
25
It seems hard to further
generalize the argument …
We need a more general approach to
prove the amazingly simple claim.
2004/2/25
Randomized Algorithms, Lecture 1
26
The subset Xi,j of X
Let Xi;j be the subset of X such that RandQS(Xi;j ) is
the ¯rst subroutine call such that its x belongs to the set
fxi ; xi+1 ; : : : ; xj g. Clearly, fxi ; : : : ; xj g µ Xi;j .
This speci¯c choice of x determines whether xi and xj will
ever be compared to each other throughout the execution
In particular, Ci;j = 1 if and only if this choice of x among
fxi ; xi+1 ; : : : ; xj g is either xi or xj . Therefore,
Pr[Ci;j
2004/2/25
2
= 1] =
:
j¡i+1
Randomized Algorithms, Lecture 1
27
For example,
X3,6 = X2,4 = X1,9
X1,3 = X1,2 = X2,3
2
7
4
8
1
9
3
6
5
3
1
2
4
8
9
7
6
5
1
2
3
5
6
7
8
9
3
5
6
8
9
1
5
2004/2/25
Randomized Algorithms, Lecture 1
X8,9
9
28
Comments about Xi,j


For each execution of RandQS(X), Xi,j is
well defined.
However, the Xi,j for two independent
execution of RandQS(X) are (very likely
to be) different.
2004/2/25
Randomized Algorithms, Lecture 1
29
So, E[C] = O(n log n)
E[C] =
X
X
n
E[Ci;j ]
i=1 j>i
=
=
X
X
n
i=1 j>i
X
X
n n¡ i
i=1µ
k=1
2
j¡i+1
2
k+1
1 1
1
· 2n 1 + + + ¢ ¢ ¢ +
2 3
n
= O(n log n)
2004/2/25
¶
Randomized Algorithms, Lecture 1
30
In summary,
The expected running time of RandQS is O(E[C]) =
O(n log n).
algorithm RandQS(X) f
if X is empty then
return;
select x uniformly at random from X;
let Y = fy 2 X j y · xg;
let Z = fz 2 X j z > xg;
call RandQS(Y );
print x;
call RandQS(Z);
g
2004/2/25
Randomized Algorithms, Lecture 1
31
Features for many
randomized algorithms

Implementation is relatively simple,
– compared to their deterministic counterparts.

The challenge for designing randomized
algorithms are usually in (asymptotic)
analysis for (time and space) complexity.
2004/2/25
Randomized Algorithms, Lecture 1
32
A misunderstanding


“The performance of randomized
algorithms depends on the distribution of
the input.”
Clarification: Not at all (for this course)
– For example, our analysis for RandQS did not
assume that n! possible permutations for the
input are given to RandQS with probability
1/(n!). More precisely, the expected running
time for RandQS is O(n log n) on ANY input.
2004/2/25
Randomized Algorithms, Lecture 1
33
RA  probabilistic analysis

Probabilistic analysis for a (deterministic
or randomized) algorithm assumes a
particular probability distribution on the
input and then studies the expected
performance of the algorithm.
2004/2/25
Randomized Algorithms, Lecture 1
34
Achilles’ heel of RA

Is there a random number generator? (That
is, can computer throw a die?)
2004/2/25
Randomized Algorithms, Lecture 1
35
Related to CMI’s
Millennium Problems



Pseudo-random generator exists if and only if
one-way function exists.
If one-way function exists, then P NP.
Anybody proving or disproving P  NP gets
US$1,000,000 from Clay Math Institute, which
raised 7 open questions in year 2000, imitating
Hilbert’s 23 open questions raised in year 1900.
2004/2/25
Randomized Algorithms, Lecture 1
36
CMI Millennium Prize

Clay Mathematics Institute (Cambridge,
MA, USA) offered US$100,000 for each
of seven open problems on May 24, 2000
at Paris.
– | Birch and Swinnerton-Dyer Conjecture |
Hodge Conjecture | Navier-Stokes Equations |
P vs NP | Poincare Conjecture | Riemann
Hypothesis | Yang-Mills Theory |
2004/2/25
Randomized Algorithms, Lecture 1
37
Simulate a fair coin
by a biased coin.

By von Neumann (1951):
– biased “head” + biased “tail”  fair “head”.
– biased “tail” + biased “head”  fair “tail”.
– Otherwise, repeat the above procedure.
2004/2/25
Randomized Algorithms, Lecture 1
38
Part 2
掃黑的藝術 (maximum cut)
2004/2/25
Randomized Algorithms, Lecture 1
39
Maximum Cut Problem

Input:
– A graph G

Output:
– A partition of G’s
nodes into A and B
that maximizes the
number of edges
between A and B.
2004/2/25
Randomized Algorithms, Lecture 1
40
Illustration
2004/2/25
Randomized Algorithms, Lecture 1
41
Intractability

The problem is NP-hard even if each node
in the input graph has no more than 3
neighbors.
Bad News
2004/2/25
Randomized Algorithms, Lecture 1
42
How “hard” is NP-hard?

So far, scientist only
knows how to solve
such a problem on an
n-node graph in O(cn)
time for some
constant c.
2004/2/25
Randomized Algorithms, Lecture 1
43
That is, …

“Impossible” to find an optimal solution
for all graphs with, say, 10000 nodes.
2004/2/25
Randomized Algorithms, Lecture 1
44
On the bright side…

If you can come up with an algorithm for
such a problem that runs in O(n1000000)
time, then you will be awarded Turing
Award for sure plus US$1,000,000 from
CMI.
2004/2/25
Randomized Algorithms, Lecture 1
45
NP-completeness
= Dead end ?
2004/2/25
Randomized Algorithms, Lecture 1
46
退一步 海闊天空
Approximation Algorithms
(近似演算法)
2004/2/25
Randomized Algorithms, Lecture 1
47
近似演算法的哲學
放下對完美的堅持,
往往就可以找到新的出路。
知所進退, 則近道矣!
2004/2/25
Randomized Algorithms, Lecture 1
48
A extremely simple
randomized approximation
For each node v of G, put v into A
with probability ½.
2004/2/25
Randomized Algorithms, Lecture 1
49
Approximation Algorithm

Criterion 1: feasibility
– output a feasible solution.

Criterion 2: tractability
– runs in polynomial time.

Criterion 3: quality
– The solution’s quality is provably not too far
from that of an optimal solution.
2004/2/25
Randomized Algorithms, Lecture 1
50
Q1: feasibility

Any partition is a feasible solution.
2004/2/25
Randomized Algorithms, Lecture 1
51
Q2: tractability

Runs in (deterministic) linear time, with
the help of a random number generator.
2004/2/25
Randomized Algorithms, Lecture 1
52
Q3: quality?


The expected approximation ratio is 2.
More precisely, we can prove that the
expected cardinality of the output cut is at
least 0.5 times that of an optimal cut.
– Note that the proof for the expected
approximation ratio does not require knowing
the cardinality of an optimal in advance.
2004/2/25
Randomized Algorithms, Lecture 1
53
Let C = the cardinality of
the output cut.
Let m be the number of edges in the input graph. Clearly,
the size of any cut, including any maximum cut, is at most
m.
We have
E[C] =
X
Pr[e is in the output cut]
edge e of G
=
m
:
2
So, the expected approximation ratio is at most 2.
2004/2/25
Randomized Algorithms, Lecture 1
54
Interesting enough,
this simple algorithm was
the best previously known
approximation until…
M. Goemans and D. Williamson,
[ACM STOC 1994]
2004/2/25
Randomized Algorithms, Lecture 1
55
A seminal paper


1/0.878-randomized approximation for
MAXCUT.
Initiate a series of research in Operations
Research, Scientific Computing, and
Approximation Algorithms.
2004/2/25
Randomized Algorithms, Lecture 1
56
Traditional approach
relaxation
Integer Linear Program
Linear Program
Approximation
Solver
Integral solution
Fractional solution
Rounding
2004/2/25
Randomized Algorithms, Lecture 1
57
SDP-based approach
relaxation
Quadratic Program
Semi-definite Program
Approximation
Solver
Scalar solution
Vector solution
Rounding
2004/2/25
Randomized Algorithms, Lecture 1
58
Remarks
勇於嘗試, 努力創新
 一篇好作品的影響, 往往遠甚於許
多普通的論文. (跳高)

2004/2/25
Randomized Algorithms, Lecture 1
59