Download Lecture 15 Randomized algorithms

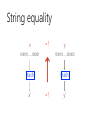
Lecture 14 Randomized algorithms
•
Introduction to Randomized algorithms
•
Primality test
Randomized algorithms
God does NOT play dice.
But
Algorithms do.
Randomized algorithm
Definition: RandomizedAlgorithm
A randomized algorithm is an algorithm which
employs a degree of randomness as part of its logic.
It may give different results when applied to the
same input in different runs.
It’s running time may be different for the same
input in different runs.
It may give wrong answers.
Example
Problem: Polynomial
Input: a polynomial expression f(x1,x2,...,xn) with n
variables.
Output: Yes, if f=0; No, otherwise.
1. Randomly choose <v1,v2,...,vn>
2. compute v = f(v1,v2,...,vn)
3. if (v==0) return ‘yes’
4.
else return ‘no’
Las Vegas v.s. Monte Carlo
Always give a correct answer.
Running time is random.
May occasionally produces
an incorrect answer.
Running time is fixed.
Las Vegas: Random sampling
Problem: RandomSampling
Input: a set of n elements
Output: randomly select m elements out of n
Analysis
• Assume we have select k-1 elements
• The probability of pick a new element:
pk = n-k+1/n, qk = 1 - pk
• Xk: the number of picks before getting a new element. Pr[Xk
= i] = pk*qki-1
• E[Xk] = pk(1+2qk+3qk2+…) = 1/pk
• T(n) = E(X1+X2+…+Xm) = n(1/n+1/(n-1)+…+1/(n-m+1)) < 1.69n
Monte Carlo: String equality
I have x.
x =? y
I have y.
String equality
x
=?
y
1010111.......100101
1010111.......100100
Hash
Hash
x’
=?
y’
String equality
Monte Carlo algorithm
Las Vegas algorithm
If x’ ≠ y’, then x ≠ y else x = y.
If x’ ≠ y’, then x ≠ y
else check x == y
x’ = x mod p, p is a prime.
String equality
1. Randomly choose a prime p < M
2. compute x’ = x mod p
3. send x’ and p to another party
x =? y
1. on receiving x’ and p
2. compute y’ = y mod p
3. if (x’ = y’) then return ‘yes’
4.
else return ‘no’
Analysis
Proposition
Let π(n) be the number of primes less than n.
1. π(n) is asymptotic to n/lnn.
2. If k < 2n and n is not very small, then the number of
distinct primes that divide k is less than π(n).
M = 2n2
Analysis
20
2
Assume x,y have
bits.
M = 2n2 = 2*240
Each finger print has 41 bits.
Pr[failure] = 1/220
M = 2n2
Where are we?
• Introduction to Randomized algorithms
• Primality test
Primality test
Problem: Primality
Input: a positive integer p
Output: ‘prime’ if p is a prime, ‘composite’ otherwise
A naive algorithm takes
Factoring an integer is a much harder problem
than primality test.
A Monte Carlo algorithm
a la Fermat’s theorem
Fermat’s Little Theorem
If n is prime, then for all a ≢0 (mod n), we have
an−1 ≡ 1 (mod n)
Carmichael number is a composite but satisfying
∀a≢0 (mod n), an-1≡ 1 (mod n)
341, 561, 1105, 1387, 1729, 1905
Pierre de Fermat (1601-1665)
source from wikipedia
Performance
It takes O(log3n).
There are only 255 Carmichael numbers less than 108.
However, there are infinite Carmichael numbers
A further improvement
Fact
If n is prime and x2 ≡ 1 (mod n). Then
x ≡ 1 (mod n) or x ≡ n − 1 (mod n)
If n is prime, am = 1, or ∃i<q, am2^i ≡ -1.
If n is composite, Pr[am = 1, or ∃i<q, am2^i ≡ -1] ≤ 1/2
A further improvement
O(log3n)
Pr[failure] ≤ 1/2
Repeat logn times, Pr[failure] ≤ 1/n
Conclusion:
Randomness helps when …
• simple deterministic heuristic with good
performance "most of the time”. (median, quicksort)
• we don't know how to do deterministically, or the
deterministic algorithms are too complex. (primality
testing, linear-time min-spanning tree.)
• we need to do things provably impossible
deterministically, or that seem impossible… (protocol
or oracle problems)
Quick sort, randomized
Expected running time: Θ(nlogn)
Selection, randomized
Expect running time: Θ(n)
References
Randomized Algorithms,
Motwani and Raghavan,
Cambridge Univ Press, 1995.
Probability and Computing:
Randomized Algorithms and
Probabilistic Analysis, Mitzenmacher
and Upfal, Cambridge Univ Press,
2005.