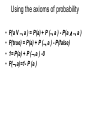Download Uncertainty

Uncertainty
Chapter 13
Outline
•
•
•
•
•
Uncertainty
Probability
Syntax and Semantics
Inference
Independence and Bayes' Rule
Uncertainty
• Lack of access to the whole truth about their
environment , an agent can’t use logical
approach only to derive plans to work.
• Agents must, therefore, act under uncertainty.
• Typical applications
– Diagnosis
• medicine, automobile repair etc
– decision-making
• Eg. Should I take my umbrella when I go out?
• handwriting recognition, law, business, design, automobile
repair, gardening, dating, and so on.
Example: wumpus world
• For example, an agent in the wumpus world of
has sensors that report only local information,
most of the world is not immediately observable.
• A wumpus agent often will find itself unable to
discover which of two squares contains a pit.
• If those squares are en route to the gold, then
the agent might have to take a chance and enter
one of the two squares.
Section 13.1. Acting under Uncertainty
Example: Catch the flight
Let action At = leave for airport t minutes before flight
Will At get me there on time?
Problems:
1.
2.
2.
3.
3.
4.
4.
5.
partial observability (road state, other drivers' plans, etc.)
noisy sensors (traffic reports)
uncertainty in action outcomes (flat tire, etc.)
immense complexity of modeling and predicting traffic
Hence a purely logical approach either
1.
2.
risks falsehood: “A25 will get me there on time”, or
leads to conclusions that are too weak for decision making:
“A25 will get me there on time if there's no accident on the bridge and it doesn't
rain and my tires remain intact etc etc.”
Handling uncertain knowledge
• Try to write rules for dental diagnosis using firstorder logic
• Wrong!
– Not all patients with toothaches have cavities; some
of them have gum disease, an abscess, or one of
several other problems:
• An almost unlimited list of possible causes is
required to make the rule true
Handling uncertain knowledge
• try turning the rule into a causal rule:
• Wrong again!
– not all cavities cause pain
• The only way to fix the rule is to make it logically
exhaustive
– to augment the left-hand side with all the qualifications required
for a cavity to cause a toothache
– must also take into account the possibility that the patient might
have a toothache and a cavity that are unconnected.
Handling uncertain knowledge
• First-order logic fails to cope with a domain like
diagnosis for three main reasons:
– Laziness
• It is too much work to list the complete set of antecedents or
consequents needed to ensure an exceptionless rule and too
hard to use such rules.
– Theoretical ignorance
• Medical science has no complete theory for the domain.
– Practical ignorance
• Even if we know all the rules, we might be uncertain
about a particular patient because not all the necessary
tests have been or can be run.
Methods for handling uncertainty
• Default or nonmonotonic非单调logic:
•
– Assume my car does not have a flat tire
–
– Assume A25 works unless contradicted by
evidence
• Issues: What assumptions are reasonable?
How to handle contradiction?
•
• Rules with fudge factors:
•
– A25 |→0.3 get there on time
–
Methods for handling uncertainty
• Probability
•
– Main method to handle uncertainty
– Model agent's degree of belief
• assigns to each sentence a numerical degree of
belief between 0 and 1.
• 0:false 1:true
• The sentence itself is in fact either true or false.
– Given the available evidence,
–
– A25 will get me there on time with
probability 0.04
Note
• A degree of belief is different from a
degree of truth.
– A probability of 0.8 does not mean "80% true"
but rather an 80% degree of belief-that is, a
fairly strong expectation.
• facts either do or do not hold in the world as logic
– Degree of truth, as opposed to degree of
belief, is the subject of fuzzy logic
Probability
Probabilistic assertions summarize effects of
– laziness: failure to enumerate exceptions, qualifications, etc.
–
– ignorance: lack of relevant facts, initial conditions, etc.
–
Subjective probability:
• Probabilities relate propositions to agent's own state
of knowledge
e.g., P(A25 | no reported accidents) = 0.06
These are not assertions about the world
Making decisions under
uncertainty（不确定）
Suppose I believe the following:
P(A25 gets me there on time | …) = 0.04
P(A90 gets me there on time | …) = 0.70
P(A120 gets me there on time | …) = 0.95
P(A1440 gets me there on time | …)
= 0.9999
• Which action to choose?
•
Depends on my preferences for missing flight vs.
time spent waiting, etc.
– Utility theory is used to represent and infer preferences
Utility theory
• Utility
—the quality of being useful
– every state has a degree of usefulness, or
utility, to an agent
– the agent will prefer states with higher utility
– The utility of a state is relative to the agent
whose preferences the utility function is
supposed to represent
• Eg. The utility of a state in which White has won a
game of chess is obviously high for the agent
playing White, but low for the agent playing Black.
Fundamental idea of decision
theory
• An agent is rational if and only if it chooses
the action that yields the highest expected
utility, averaged over all the possible
outcomes of the action.
• This is called the principle of Maximum
Expected Utility (MEU).
Design for a decision-theoretic
agent
Section 13.2. Basic Probability Notation
Syntax
• Basic element: random variable随机变量
• Similar to propositional logic: possible worlds defined by
assignment of values to random variables.
• Boolean random variables
•
e.g., Cavity (do I have a cavity?)
• Discrete random variables
•
e.g., Weather is one of <sunny,rainy,cloudy,snow>
• Domain values must be exhaustive and mutually exclusive
• Elementary proposition constructed by assignment of a value
to a random variable: e.g., Weather = sunny, Cavity = false
• (abbreviated as cavity)
Syntax
• Atomic event: A complete specification of the
state of the world about which the agent is
uncertain
•
E.g., if the world consists of only two Boolean
variables Cavity and Toothache, then there are 4
distinct atomic events:
Cavity = false Toothache = false
Cavity = false  Toothache = true
Cavity = true  Toothache = false
Cavity = true  Toothache = true
• Atomic events are mutually exclusive（互斥
Section 13.2. Basic Probability Notation
Prior probability（先验概率）
•
•
Prior or unconditional probabilities of propositions
e.g., P(Cavity = true) = 0.1 and P(Weather = sunny) = 0.72 correspond to belief
prior to arrival of any (new) evidence
•
•
Probability distribution gives values for all possible assignments:
P(Weather) = <0.72,0.1,0.08,0.1> (normalized, i.e., sums to 1，Statistic
results)
•
Joint probability distribution(联合概率分布） for a set of random
variables gives the probability of every atomic event on those random
variables
•
P(Weather,Cavity) = a 4 × 2 matrix of values:
Weather =
Cavity = true
Cavity = false
sunny
0.144
0.576
rainy
0.02
0.08
cloudy snow
0.016
0.02
0.064
0.08
probability density functions
• Probability distributions for continuous variables are
called probability density functions.
• For continuous variables, it is not possible to write out
the entire distribution as a table. (infinitely many values!)
• defines the probability that a random variable takes on
some value x as a parameterized function of x
– For example, let the random variable X denote tomorrow's
maximum temperature in Berkeley.
– Then the sentence
• P(X = x ) = U[18,26] ( x )
expresses the belief that X is distributed uniformly between 18
and 26 degrees Celsius.
– P ( X = 20.5) = U[18,26] (20.5) == 0.125/C.
• The probability that the temperature is in a small region around 20.5
degrees is equal, in the limit, to 0.125 divided by the width of the
region in degrees Celsius:
Conditional probability（条件概率）
• Conditional or posterior probabilities（后验概率）
•
e.g., P(cavity | toothache) = 0.8
i.e., given that all I know is toothache
• If we know more, e.g., cavity is also given, then we
have
•
P(cavity | toothache,cavity) = 1
• New evidence may be irrelevant, allowing
simplification, e.g.,
•
P(cavity | toothache, sunny) = P(cavity | toothache) = 0.8
Conditional probability
• Definition of conditional probability:
•
P(a | b) = P(a  b) / P(b) if P(b) > 0
• Product rule gives an alternative formulation:
•
P(a  b) = P(a | b) P(b) = P(b | a) P(a)
• A general version holds for whole distributions, e.g.,
•
P(Weather,Cavity) = P(Weather | Cavity) P(Cavity)
• (View as a set of 4 × 2 equations, not matrix mult.)
•
• Chain rule is derived by successive application of product rule:
•
Section 13.3. The Axioms of Probability
Axioms of probability（概率公理）
• For any propositions A, B
•
– 0 ≤ P(A) ≤ 1
– P(true) = 1 and P(false) = 0
– P(A  B) = P(A) + P(B) - P(A  B)
–
Using the axioms of probability
•
•
•
•
P(a V  a ) = P(a) + P ( a ) - P(a ∧  a )
P(true) = P(a) + P ( a ) - P(false)
1= P(a) + P ( a ) -0
P( a)=1- P (a )
Using the axioms of probability
• Let the discrete variable D have the
domain (d1, . . . , dn,).
Section 13.4. Inference Using Full Joint Distributions
Inference by enumeration
• example: a domain consisting of three Boolean
variables Toothache, Cavity, and Catch (the dentist's
nasty steel probe catches in my tooth).
• Start with the joint probability distribution:
•
• For any proposition φ, sum the atomic events where
it is true: P(φ) = Σω:ω╞φ P(ω)
Inference by enumeration
• Start with the joint probability distribution:
•
• For any proposition φ, sum the atomic events where
it is true: P(φ) = Σω:ω╞φ P(ω)
•
• P(toothache) = 0.108 + 0.012 + 0.016 + 0.064 = 0.2
•
Inference by enumeration
• Start with the joint probability distribution:
•
• For any proposition φ, sum the atomic events where
it is true: P(φ) = Σω:ω╞φ P(ω)
•
• P(toothacheV cavity ) = 0.108 + 0.012 + 0.016 +
0.064+0.072+ 0.008= 0.28
•
Inference by enumeration
• Start with the joint probability distribution:
•
• Can also compute conditional probabilities:
•
P(cavity | toothache) = P(cavity  toothache)
P(toothache)
=
0.016+0.064
0.108 + 0.012 + 0.016 + 0.064
= 0.4
Inference by enumeration
• Start with the joint probability distribution:
•
• Another way to calculate P(cavity | toothache) :
•
P(cavity | toothache) = P(cavity  toothache)
P(toothache)
=
0.108+0.012
0.108 + 0.012 + 0.016 + 0.064
= 0.6
P(cavity | toothache) =1-P(cavity | toothache)=0.4
Normalization
• In previous examples, 1/P(toothache) can be viewed as a
normalization constant αfor the distribution P( Cavity /
toothache), ensuring that it adds up to 1.
•
P(Cavity | toothache) = αP(Cavity,toothache)
= α[P(Cavity,toothache,catch) + P(Cavity,toothache, catch)]
= α[<0.108,0.016> + <0.012,0.064>]
= α <0.12,0.08> = <0.6,0.4>
General idea: compute distribution on query variable by fixing
evidence variables and summing over hidden variables(not
Inference by enumeration,
contd.
Typically, we are interested in
the posterior joint distribution of the query variables
X
given specific values e for the evidence variables E
Let the hidden variables be Y (remain unobserved
variables)
Then the required summation of joint entries is done
by summing out the hidden variables:
P(X| e) = αP(X,e) = αΣyP(X, e, y)
Section 13.5. Independence
Independence
• A and B are independent iff
P(A|B) = P(A) or P(B|A) = P(B)
P(B)
or P(A, B) = P(A)
P(Toothache, Catch, Cavity, Weather)
= P(Toothache, Catch, Cavity) P(Weather)
• 32 entries reduced to 12;
• (32=2*2*2*4,12=2*2*2+4)
Independence
• Independence assertions are usually
based on knowledge of the domain.
• can dramatically reduce the amount of
information necessary to specify the full
joint distribution
• If the complete set of variables can be
divided into independent subsets, then the
full joint can be factored into separate joint
distributions on those subsets.
Section 13.5. Independence
Independence
• for n independent biased coins
O(2n) →O(n)
• Absolute independence powerful but rare
•
• Dentistry is a large field with hundreds of variables,
none of which are independent. What to do?
•
13.6 BA.YES' RULE AND ITS USE
Bayes' Rule
• Product rule P(ab) = P(a | b) P(b) = P(b | a) P(a)
•
 Bayes' rule: P(a | b) = P(b | a) P(a) / P(b)
• or in distribution form
•
P(Y|X) = P(X|Y) P(Y) / P(X) = αP(X|Y) P(Y)
• Useful for assessing diagnostic probability from
causal probability:
•
– P(Cause|Effect) = P(Effect|Cause) P(Cause) / P(Effect)
–
– E.g., let M be meningitis, S be stiff neck:
Bayes' Rule and conditional
independence
P(Cavity | toothache  catch)
= αP(toothache  catch | Cavity) P(Cavity)
= αP(toothache | Cavity) P(catch | Cavity) P(Cavity)
• This is an example of a naïve Bayes model(Bayesian
classifier):
•
P(Cause,Effect1, … ,Effectn) = P(Cause) πiP(Effecti|Cause)
naïve Bayes model
• The model is called "naive" because it is
often used (as a simplifying assumption) in
cases where the "effect" variables are not
conditionally independent given the cause
variable.
• In practice, naive Bayes systems can work
surprisingly well, even when the
independence assumption is not true.
13.6 BA.YES' RULE AND ITS USE
Conditional independence
•
P(Toothache, Cavity, Catch) has 23 – 1 = 7 independent entries
• (because the numbers must sum to 1)
•
•
•
If I have a cavity, the probability that the probe catches in it doesn't
depend on whether I have a toothache:
•
(1) P(catch | toothache, cavity) = P(catch | cavity)
•
•
The same independence holds if I haven't got a cavity:
•
•
Catch is conditionally independent of Toothache given Cavity:
(2) P(catch | toothache,cavity) = P(catch | cavity)
P(Catch | Toothache,Cavity) = P(Catch | Cavity)
•
Equivalent statements:
Conditional independence
contd.
• Write out full joint distribution using chain rule:
•
P(Toothache, Catch, Cavity)
= P(Toothache | Catch, Cavity) P(Catch, Cavity)
= P(Toothache | Catch, Cavity) P(Catch | Cavity) P(Cavity)
= P(Toothache | Cavity) P(Catch | Cavity) P(Cavity)
• In most cases, the use of conditional independence
reduces the size of the representation of the joint
distribution from exponential in n to linear in n.
•
Summary
• Probability is a rigorous formalism for
uncertain knowledge
•
• Joint probability distribution specifies
probability of every atomic event
• Queries can be answered by summing over
atomic events
•
• For nontrivial domains, we must find a way
to reduce the joint size
•
• Independence and conditional independence