* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download 235_lecture6_080219
Birthday problem wikipedia , lookup
Corecursion wikipedia , lookup
Generalized linear model wikipedia , lookup
Regression analysis wikipedia , lookup
Least squares wikipedia , lookup
Fisher–Yates shuffle wikipedia , lookup
Hardware random number generator wikipedia , lookup
Probability box wikipedia , lookup
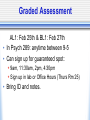
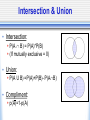
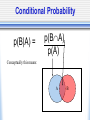
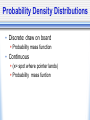
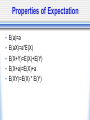
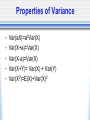
Psyc 235: Introduction to Statistics DON’T FORGET TO SIGN IN FOR CREDIT! (and check out the lunar eclipse on Thursday from about 9-10) Graded Assessment AL1: Feb 25th & BL1: Feb 27th • In Psych 289: anytime between 9-5 • Can sign up for guaranteed spot: 9am, 11:30am, 2pm, 4:30pm Sign up in lab or Office Hours (Thurs Rm 25) • Bring ID and notes. Graded Assessment • ALEKS will be unavailable: AL1: 8am Mon - 11:59pm Wed BL1: 8am Wed - 11:59pm Fri • Conflict/Makeup exams: must be within that window let us know ASAP (as in TODAY) Quiz on this Thursday • Use this quiz as practice exam for the assessment. • Get your notes ready beforehand. • Complete like an assessment • Make note of trouble areas, additional notes you would like, etc. • Can do the quiz in office hours and then ask Jason questions Questions? Intersection & Union • Intersection: P(A B) = P(A)*P(B) (If mutually exclusive = 0) • Union: P(A U B) =P(A)+P(B)- P(AB) • Compliment: p(A)=1-p(A) Independent vs. Dependent Events • Independent Events: unrelated events that intersect at chance levels given relative probabilities of each event • Dependent Events: events that are related in some way Concepts of union and intersection are the same However, P(AB) P(A)*P(B) • Do you think mutually exclusive events are dependent or independent? Conditional Probability p(B|A) = p(BA) p(A) Conceptually this means: A B Baye’s Theorem p(B|A) = p(A|B)p(B) p(A|B)p(B) + p(A|B)p(B) • Can we break this down a little to understand it better? • p(A|B)*p(B)=p(AB) A • p(A|B)*p(B) + p(A|B)*p(B) = p(AB) + p(AB) = p(A) p(B|A) = •So, this is just: p(BA) p(A) B Law of Total Probabilities A B • p(A) = p(AB) + p(AB) • p(A) = p(A|B)p(B) + p(A|B)p(B) _ B Random Variables • Where are we? • In set theory, we were talking about theoretical variables that only took on two values: either a 0 or 1. They were in the group or not. • Now we’re going to talk about variables that can take on multiple values. Random Variables • But wait, didn’t we already talk about variables that had multiple values? • When we were talking about central tendancy and dispersion, we were talking about specific distributions of data…now we’re going to start discussing theoretical distributions. Data World vs. Theory World • Theory World: Idealization of reality (idealization of what you might expect from a simple experiment) Theoretical probability distribution • Data World: data that results from an actual simple experiment Frequency distribution But First… • Before we get into random variables, we need to spend a little bit of time thinking about: the kinds of values variables can take on what those values mean how we can combine them 4 Standard Scales • Categorical (Nominal) Scale Numbers serve only as labels Only relevant info is frequency • Ordinal Scale Things that are ranked Numbers give you order of items, but not distance between/relation between • Interval Scale Scale with arbitrary 0 point and arbitrary units However, units give you proportional relationship between values • Ratio Scale Scale has an absolute 0 point Intervals between units is constant What kind of scale is this? • • • • • • Temperature Grades Number Scale Terror Alert Scale Class Rank What are other scales you are familiar with? Discrete vs. Continuous Random Variables • Discrete Finite number of outcomes (x = sum of dice) Countable infinite number of outcomes Numbers from 1 to infinity • Continuous Uncountably Infinite (x=number of flips to get a head) (Convergent series: the sum of 1-infinity approaches some value) Probability Density Distributions • Discrete: draw on board Probability mass function • Continuous (x= spot where pointer lands) Probability mass funtion Next: • Now that we know more about random variables, we can apply everything that we’ve learned so far. • Graphing and displaying data • Central tendency & dispersion • Transformations of mean and variance • Contingency Tables Central Tendency in Random Variables • E(x)=∑(X*p(x)) • Var(x)=∑((X-E(x))2*p(x)) Properties of Expectation • • • • • E(a)=a E(aX)=a*E(X) E(X+Y)=E(X)+E(Y) E(X+a)=E(X)+a E(XY)=E(X) * E(Y) Properties of Variance • • • • • Var(aX)=a2Var(X) Var(X+a)=Var(X) Var(X-a)=Var(X) Var(X+Y)= Var(X) + Var(Y) Var(X2)=E(X)+Var(X)2 Contingency Tables for 2 random variables A(yes) not A (no) B (yes) p(a) p(b) p(a+b) not B(no) p(c) p(d) p(c+d) p(a+c) p(b+d) 1 • A is facilitative of B when p(B|A)>P(B) • A is inhibitory for B when p(B|A)<P(B) Remember • 1st Exam Feb 25/27 Sign up for exam timeslots in lab Wed or Office Hours Thurs (or also first-come-first-served on exam day) • Quiz on Thursday