Computational Methods in Finance
... Problem: generate random variables from specific distribution Matlab, Excel,… provide the uniform random number generator This selects uniformly a number between 0 and 1 We use the inverse cumulative function of the distribution ...
... Problem: generate random variables from specific distribution Matlab, Excel,… provide the uniform random number generator This selects uniformly a number between 0 and 1 We use the inverse cumulative function of the distribution ...
Investor Sentiment and the Mean
... perhaps the fundamental risk-return tradeoff in finance – exhibits a strong two-regime pattern and that investor sentiment has a unique capacity to distinguish these two regimes. It is hard to explain these results within the traditional asset pricing theories. Early models such as Merton’s ICAPM gen ...
... perhaps the fundamental risk-return tradeoff in finance – exhibits a strong two-regime pattern and that investor sentiment has a unique capacity to distinguish these two regimes. It is hard to explain these results within the traditional asset pricing theories. Early models such as Merton’s ICAPM gen ...
Dividend yields, dividend growth, and return predictability
... There is a generalized conviction that variation in dividend yields is exclusively related to expected returns and not to expected dividend growth—e.g. Cochrane’s presidential address (Cochrane (2011)). We extend the analysis conducted in Cochrane (2008, 2011) to equity portfolios sorted on size and ...
... There is a generalized conviction that variation in dividend yields is exclusively related to expected returns and not to expected dividend growth—e.g. Cochrane’s presidential address (Cochrane (2011)). We extend the analysis conducted in Cochrane (2008, 2011) to equity portfolios sorted on size and ...
Implied expected returns and the choice of a mean-variance
... known and a covariance matrix has been accurately estimated, the above-mentioned linear relation can be exploited to create implied expected returns which have a higher accuracy than sample means. The idea of reverse engineering for expected returns was first advocated by Best and Grauer (1985), and ...
... known and a covariance matrix has been accurately estimated, the above-mentioned linear relation can be exploited to create implied expected returns which have a higher accuracy than sample means. The idea of reverse engineering for expected returns was first advocated by Best and Grauer (1985), and ...
ISE Option Traders Statistics with Applications to Options
... What is Value-at-Risk? Value-at-risk (abbreviated either VAR or VaR) is a measure of risk that boils risk down to a single easy-to-understand number. Simply put, an option trader’s VAR is the maximum number of dollars that the trader might lose over a specified period of time (called the risk horizo ...
... What is Value-at-Risk? Value-at-risk (abbreviated either VAR or VaR) is a measure of risk that boils risk down to a single easy-to-understand number. Simply put, an option trader’s VAR is the maximum number of dollars that the trader might lose over a specified period of time (called the risk horizo ...
Optimal strategies of hedging portfolio of unit
... risky. However, they will be inclined to change their choice if an additional amount is proposed to them. This amount is the risk premium. Fair value must integrate this risk premium as this is what reflects the risk adverse character of investors on the markets. The incorporation of this risk premi ...
... risky. However, they will be inclined to change their choice if an additional amount is proposed to them. This amount is the risk premium. Fair value must integrate this risk premium as this is what reflects the risk adverse character of investors on the markets. The incorporation of this risk premi ...
Downside Risk Neutral Probabilities
... to work directly with the utility function u, and to use the stochastic discount factor formula. The price of an asset is then the expectation of its payoff, as weighted state-by-state by the relative marginal utility of wealth in this state. Another (equivalent) approach is to adjust the probabilit ...
... to work directly with the utility function u, and to use the stochastic discount factor formula. The price of an asset is then the expectation of its payoff, as weighted state-by-state by the relative marginal utility of wealth in this state. Another (equivalent) approach is to adjust the probabilit ...
On the pricing and hedging of volatility derivatives 1 Introduction
... where Wt is Brownian motion. For the rest of the paper we fix notation as follows: the conditional expectation at time t is denoted by Et = E[·|Ft ] where Ft is the filtration up to time t and E0 is thus the initial value of the expectation. All expectations are considered with respect to the risk-n ...
... where Wt is Brownian motion. For the rest of the paper we fix notation as follows: the conditional expectation at time t is denoted by Et = E[·|Ft ] where Ft is the filtration up to time t and E0 is thus the initial value of the expectation. All expectations are considered with respect to the risk-n ...
CHAPTER 11
... OVERVIEW In the index model, the return on the market portfolio summarized the broad impact of macro factors. Sometimes, however, rather than using a market proxy, it is more useful to focus directly on the ultimate sources of risk. This can be useful in risk assessment, for example, when measurin ...
... OVERVIEW In the index model, the return on the market portfolio summarized the broad impact of macro factors. Sometimes, however, rather than using a market proxy, it is more useful to focus directly on the ultimate sources of risk. This can be useful in risk assessment, for example, when measurin ...
Dual characterization of properties of risk measures on Orlicz hearts
... The purpose of this paper is to give characterizations of properties of risk measures that can be used to analyze particular examples. We first extend earlier representation results for risk measures on Orlicz hearts. Then we give general conditions for monetary risk measures to be Gâteaux-differen ...
... The purpose of this paper is to give characterizations of properties of risk measures that can be used to analyze particular examples. We first extend earlier representation results for risk measures on Orlicz hearts. Then we give general conditions for monetary risk measures to be Gâteaux-differen ...
Robust Growth-Optimal Portfolios
... of Roll’s insight that a number of mean-variance efficient portfolios lead to almost sure ruin if the available capital is infinitely often reinvested and returns are serially independent (Roll 1973, p. 551). The Markowitz approach also burdens investors with specifying their utility functions, whic ...
... of Roll’s insight that a number of mean-variance efficient portfolios lead to almost sure ruin if the available capital is infinitely often reinvested and returns are serially independent (Roll 1973, p. 551). The Markowitz approach also burdens investors with specifying their utility functions, whic ...
The Proper Use of Risk Measures in Portfolio Theory
... and wealth under risk. For example, convexity is a property that identifies the importance of diversification. Undiversified portfolios present a greater grade of uncertainty and a larger wealth under risk. Similarly, positive homogeneity implies that when wealth under risk is multiplied by a positi ...
... and wealth under risk. For example, convexity is a property that identifies the importance of diversification. Undiversified portfolios present a greater grade of uncertainty and a larger wealth under risk. Similarly, positive homogeneity implies that when wealth under risk is multiplied by a positi ...
Portfolio Value-at-Risk Using Regular Vine Copulas
... There are several methods that allow modeling joint distributions and a large fraction of them are using linear correlation. However, linear correlation can be misleading and it is important to know a dependence structure between the assets of interest. In this case copulas can be a very useful conc ...
... There are several methods that allow modeling joint distributions and a large fraction of them are using linear correlation. However, linear correlation can be misleading and it is important to know a dependence structure between the assets of interest. In this case copulas can be a very useful conc ...
Components of Target Capital for Life Companies
... “For our risk and investment strategy we need to be able to quantify the cash flow structure and the risk bearing capacity of our portfolios. For this the SST is a good (although in many aspects still to be modified and enhanced) basis. In addition, we can use the SST to test capital requirements fo ...
... “For our risk and investment strategy we need to be able to quantify the cash flow structure and the risk bearing capacity of our portfolios. For this the SST is a good (although in many aspects still to be modified and enhanced) basis. In addition, we can use the SST to test capital requirements fo ...
Stock Return Serial Dependence and Out-of
... with high (low) returns over the last twelve months tend to have high (low) returns for the next six months, and that “strategies which buy stocks that have performed well in the past and sell stocks that have performed poorly in the past generate significant positive returns over 3- to 12-month hol ...
... with high (low) returns over the last twelve months tend to have high (low) returns for the next six months, and that “strategies which buy stocks that have performed well in the past and sell stocks that have performed poorly in the past generate significant positive returns over 3- to 12-month hol ...
Financial Applications of Copula Functions
... As noted by Embrechts, McNeil and Straumann [2002], the correlation is a special case through all measures that are available to understand the relationships between all the risks. If we assume a Normal copula3 , the empirical correlation is a good measure of the dependence only if the margins are G ...
... As noted by Embrechts, McNeil and Straumann [2002], the correlation is a special case through all measures that are available to understand the relationships between all the risks. If we assume a Normal copula3 , the empirical correlation is a good measure of the dependence only if the margins are G ...
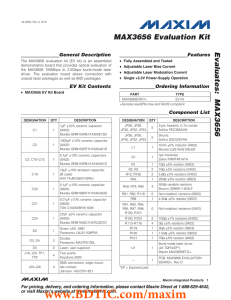
MAX3656 Evaluation Kit Evaluates: General Description Features
... external resistance between the APCSET pin and GND when a shunt is installed on the VAR side of jumper JP33. Turning the variable resistor clockwise increases the average optical power. This jumper connects a fixed resistance (R61, not installed) or a variable resistance (R119 + R59) between the MOD ...
... external resistance between the APCSET pin and GND when a shunt is installed on the VAR side of jumper JP33. Turning the variable resistor clockwise increases the average optical power. This jumper connects a fixed resistance (R61, not installed) or a variable resistance (R119 + R59) between the MOD ...
Bank Indonesia Jakarta
... This paper will discuss market risk in banks as the basis for determining capital adequacy, focusing on the variety of bank risks associated with volatility of market rates and prices. The purpose of the paper is to identify the best approach to calculating market risk for Indonesian banks and to pr ...
... This paper will discuss market risk in banks as the basis for determining capital adequacy, focusing on the variety of bank risks associated with volatility of market rates and prices. The purpose of the paper is to identify the best approach to calculating market risk for Indonesian banks and to pr ...
es09 Smets 11171430 en
... most of the variability in implied volatility, whereas both uncertainty and risk aversion determine credit spreads. In this paper, we will not do a formal decomposition using an asset pricing model. Instead, we use a simple VAR to better understand the e¤ects of innovations in uncertainty and …nanci ...
... most of the variability in implied volatility, whereas both uncertainty and risk aversion determine credit spreads. In this paper, we will not do a formal decomposition using an asset pricing model. Instead, we use a simple VAR to better understand the e¤ects of innovations in uncertainty and …nanci ...
Chapter 20
... What are the differences and similarities between the various portfolio performance measures? When we evaluate a sample of portfolios, how do we determine how well diversified they are? How do the various performance measures relate to each other in terms of rankings? ...
... What are the differences and similarities between the various portfolio performance measures? When we evaluate a sample of portfolios, how do we determine how well diversified they are? How do the various performance measures relate to each other in terms of rankings? ...
2. Return
... investors prefer the lowest possible risk, that is, investors are risk averse, (ii) for a given level of risk, investors always prefer the highest possible return. This property is referred to as nonsatiation, and (iii) the first two moments of the distribution of an asset’s return are sufficient to ...
... investors prefer the lowest possible risk, that is, investors are risk averse, (ii) for a given level of risk, investors always prefer the highest possible return. This property is referred to as nonsatiation, and (iii) the first two moments of the distribution of an asset’s return are sufficient to ...
Value at risk
VaR redirects here. For the statistical technique VAR, see Vector autoregression. For the statistic denoted Var or var, see Variance.In financial mathematics and financial risk management, value at risk (VaR) is a widely used risk measure of the risk of loss on a specific portfolio of financial exposures. For a given portfolio, time horizon, and probability p, the p VaR is defined as a threshold loss value, such that the probability that the loss on the portfolio over the given time horizon exceeds this value is p. This assumes mark-to-market pricing, and no trading in the portfolio.For example, if a portfolio of stocks has a one-day 5% VaR of $1 million, there is a 0.05 probability that the portfolio will fall in value by more than $1 million over a one day period if there is no trading. Informally, a loss of $1 million or more on this portfolio is expected on 1 day out of 20 days (because of 5% probability). A loss which exceeds the VaR threshold is termed a ""VaR break.""VaR has four main uses in finance: risk management, financial control, financial reporting and computing regulatory capital. VaR is sometimes used in non-financial applications as well.Important related ideas are economic capital, backtesting, stress testing, expected shortfall, and tail conditional expectation.