Download Week 13

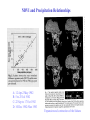
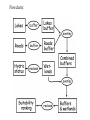
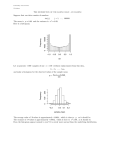
1. Simple statistical measures
• Estimating Mean and Variance
• Histogram
• Simple Linear Regression
2. Cartographic modeling
Simple statistical measures
• Estimating Mean and Variance
• Histogram
• Simple Linear Regression
Estimating Mean and Variance
The formulae given before to calculate the mean and variance requires to know
all the probability mass function or probability density function for all possible
measurements (or the entire population). In reality we often do not know them
a priori because the size of the population may be very big or infinite. The way
to get information about the mean and variance for a population is to take a
sample and infer from there.
Given a sample of x1,x2, …, xn randomly taken from a population, the population
mean and variance are estimated from the sample as in the following
1 n
ˆ   xi
n i 1
n
1
2
ˆ
ˆ 2 
(
x


)
 i
n  1 i 1
Why Squared?
The variance is the average squared difference of an individual
value from the population mean. Why squared?
Example cases: Suppose we want to evaluate two GPS receivers for their accuracy.
We take the receivers out to measure the distance between two points that are
exactly 100.00 meters. We take 5 reading using each GPS and the following are
the distance:
Receiver1: 103, 97, 105 93 102
Receiver 2: 101, 100, 99, 98 103
They both give an average distance of 100.00 m. Are there
difference in their accuracy?
What are the variances for each receiver?
Answer
Receiver 1:

1 N
1
2
s 
(
x

x
)

(103  100) 2  (97  100) 2  (105  100) 2  (93  100) 2  (102  100) 2

i
N  1 i 1
4
2




1
(3) 2  (3) 2  (5) 2  (7) 2  (2) 2  24.0
4
Receiver 2:

1 N
1
2
s 
(
x


)

(101  100) 2  (100  100) 2  (99  100) 2  (98  100) 2  (103  100) 2

i
N  1 i 1
4
2



1 2
(1)  (0) 2  (1) 2  (2) 2  (3) 2  3.75
4

Histogram
The mean and variance tell us the overall magnitude and variation of
data in a sample. An graphic view about the same information is
called a histogram. A Histogram is a graph that shows the frequency
for all the data observed in a sample. For Example, the following table
shows the frequency distribution for a Geog370 midterm. The graph to
the right is the histogram showing the frequency distribution.
Frequency
Ratings
80s
70s
60s
50s
20s
Frequency
10
14
7
3
1
14
10
7
3
20
50 60 70 80
Grades
Histogram Shapes
Bell Shape
Bimodal
Mode: value with highest frequency
Range: largest value-smallest value
Skewed
Random
The definition of relative frequency probability tells that if we increase the number
of observations for the random variable, the relative frequency of the histogram
gets increasingly closer to its probability distribution.
Histogram
Landsat TM 1993
Landsat ETM 2002
Mode
Mode is defined as the peak of the frequency distribution or the
most frequent class.
Median
The median of a set of n observations, x1, x2, …, xn is defined
to be the central value when the observations are arranged in
order of magnitude. If there is an even number of observations,
the median value is the midpoint between the two center
observations
Standard Deviation
Square root of variance, which express the variability in measurement
of the original units.
Skewness:
measure the degree of asymmetry about the mean of the data.
Simple Linear Regression
In the previous slides, we only focus on one random variable. In many
applications, we often work with a pair of variables. For example the
distance travels and the time spent driving; one’s age and height.
Generally, there are two types of relationships between a pair of variable:
deterministic relationship and probabilistic relationship.
Deterministic relationship
s  s0  vt
S: distance travel
S0: initial distance
v: speed
t: traveled
distance
slope
S0
v
intercept
time
Probabilistic Relationship
In many occasions we are facing a different situation. One variable is
related to another variable as in the following.
height
age
Here we can not definitely to predict one’s height from his age as we did
in
s  s0  vt
Linear Regression
Statistically, the way to characterize the relationship between two variables
as we shown before is to use a linear model as in the following:
y  a  bx  
Here, x is called independent variable
y is called dependent variable
 is the error term
y
a is intercept
b is slope
Error: 
b
a
x
Least Square Lines
Given some pairs of data for independent and dependent variables,
we may draw many lines through the scattered points
y
x
The least square line is a line passing through the points that minimize the
vertical distance between the points and the line. In other words, the least
square line minimizes the error term .
Least Square Method
For notational convenience, the line that fits through the
points is often written as
yˆ  a  bx
The linear model we wrote before is
y  a  bx  
If we use the value on the line, ŷ , to estimate y, the difference is (y- ŷ)
For points above the line, the difference is positive, while the difference
is negative for points below the line.
y
yˆ  a  bx
ŷ
(y- ŷ)
Sum of Squares error
For some points, the values of (y- ŷ) are positive (points above the line) and for some
other points, the values of (y- ŷ) are negative (points below the line). If we add all
these up, the positive and negative values can get cancelled. Therefore, we take a
square for all these difference and sum them up. Such a sum is called the Error Sum
of Squares (SSE)
n
SSE   ( y  yˆ ) 2
i 1
The constant a and b is estimated so that the error sum of squares is
minimized, therefore the name least squares.
Estimating Regression Coefficients
If we solve the regression coefficients a and b from by minimizing SSE,
the following are the solutions.
n
b
 ( x  x )( y  y )
i
i 1
i
n
2
(
x

x
)
 i
i 1
a  y  bx
Where xi is the ith independent variable value
yi is dependdent variable value corresponding to xi
x_bar and y_bar are the mean value of x and y.
Interpretation of a and b
The constant b is the slope, which gives the change in y (dependent variable) due to a
change of one unit in x (independent variable). If b> 0, x and y are positively correlated,
meaning y increases as x increases, vice versus. If b<0, x and y are negatively correlated.
y
y
a
a
b<0
b>0
x
x
Correlation Coefficient
Although now we have a regression line to describe the relationship between the
dependent variable and the independent variable, it is not enough to characterize
the relationship between x and y. We may see the situation in the following graphs.
y
(a)
y
x
(b)
x
Obviously the relationship between x and y in (a) is stronger than that in (b) even
though the line in (b) is the best fit line. The statistic that characterizes the strength
of the relationship is correlation coefficient or R2
R Square
Regression Sum of Squares
y
n
SSR   ( yˆ i  y )
2
ŷ
i 1
Total Sum of Squares
n
SST   ( yi  y ) 2
i 1
R2 
SSR
SST
R square indicates the percent variance in y explained by the regression.
y
An Simple Linear Regression Example
The followings are some survey data showing how much a family spend on
food in relation to household income (x=income in thousand $, y=$ on food)
x
y
6.5
81
4
96
2.5
93
7.2
68
8.1
63
3.4
84
5.5
71
sum
37.2
556
mean
5.31429 79.4286
slope
-5.2071
intercept 107.101
SST
953.714
SSR
706.834
SSE
246.881
SST+SSR 953.715
R-square 0.74114
x-x_bar
1.185714
-1.31429
-2.81429
1.885714
2.785714
-1.91429
0.185714
y-y_bar
(x-x_bar)(y-y_bar)
1.571429
1.863265306
16.57143
-21.77959184
13.57143
-38.19387755
-11.4286
-21.55102041
-16.4286
-45.76530612
4.571429
-8.751020408
-8.42857
-1.565306122
-135.7428571
(x-x_bar)^2
1.40591837
1.72734694
7.92020408
3.55591837
7.76020408
3.6644898
0.0344898
26.0685714
y_hat
73.254325
86.2722
94.082925
69.60932
64.922885
89.39649
78.461475
(y-y_bar)^2 (y_hat-y_bar)^2 (y-y_hat)^2
2.46938776
38.12130132
59.99548121
274.612245
46.83527158
94.63009284
184.183673
214.7501205
1.172726556
130.612245
96.41767056
2.589910862
269.897959
210.4148973
3.697486723
20.8979592
99.35942913
29.12210432
71.0408163
0.935272739
55.67360918
953.714286
706.8339631
246.8814117
NDVI and Precipitation Relationships
A: 12 Apr-2 May 1982
B: 5 to 25 Jul 1982
C: 22 Sep to 17 Oct 1982
D: 10 Dec 1982-9Jan 1983
Expansion and contraction of the Sahara
• How the various properties of a location are
related is an important aspect of the nature of
geographic data
Y=f(x1,x2,x3,…,xk)
Y: the value of individual properties in a city
X1:floor area
X2: distance to parks
X3: distance to schools
….
Spatial autocorrelation
• “Spatial autocorrelation is determined both
by similarities in position, and by
similarities in attributes”
• The Tobler Law: everything is related to
everything else, but near things are more
related than distant things.
Spatial autocorrelation
• Positive spatial autocorrelation:
Features that are similar in location are also similar in
attributes
• Negative spatial autocorrelation:
Features that are similar in location are dissimilar in
attributes
• Zero autocorrelation
Features are independent of location
• Cartographic modeling
“A cartographic model provides
information through a combination of
spatial data sets, functions, and operations”
Functions and operations: reclassification,
overlay, interpolation, terrain analyses,
buffering and other proximity functions.
Cartographic models: an example
• Suitability analyses are perhaps the most
common examples of cartographic models.
• Suitability analyses rank land according to
their utility for various uses.
Cartographic models: an example
• Suitable sites:
(a) near lakes
(b) near roads
(c) not wetland
Cartographic models: an example
• Data
Lakes, roads, and hydric status
• Spatial operations
Buffering, reclassification, and overlay
Flowcharts:
Cartographic models: weightings among criteria
Criteria for a home-site selection:
1) Slopes should not be too steep
2) Sites should be far enough from a main
road to offer some privacy, but not so far as
to be isolated.
3) ?
The conversion from a qualitative to quantitative specification?
Weightings among criteria
• How to combine distinct criteria?
- Overlay
- Addition
We must choose how to weight one layer
relative to another.
Home-site selection:
- How important is isolation relative to other
factors
It is often difficult to assign the relative
weights in an objective fashion
•
One methods of assigning weights is based on
their importance ranking.
1. Rank the importance
2. Calculate the relative weights according to: