Download Document

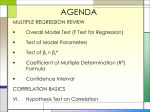
AGENDA
MULTIPLE REGRESSION BASICS

Overall Model Test (F Test for Regression)

Test of Model Parameters

Test of βi = βi*

Coefficient of Multiple Determination (R2)
Formula

Confidence Interval
CORRELATION BASICS
VI.
Hypothesis Test on Correlation
Multiple Regression Basics
Y=b0 + b1X1 + b2X2 +…bkXk
 Where Y is the predicted value of Y,
the value lying on the estimated
regression surface. The terms b0,…,k
are the least squares estimates of the
population regression parameters ßi
I. ANOVA Table for Regression Analysis
Source of
Variation
Regression
Residual
Total
Degrees of Sums of
Freedom Squares
Mean Squares
F
MSR/ MSE
k
SSR
MSR = SSR / k
n-k-1
SSE
MSE=SSE/(n-k-1)
n-1
SST
II. Test of Model Parameters
H0:
H1:
β1= 0
β1 ≠ 0
t-calc =
No Relationship
Relationship
bi   i
S bi
n = sample size
t-critical:
 t / 2,nk 1
III. Test of βi = βi*
H0:
H1:
t-calc =
n=
t-critical:
β1= βi*
β1≠ βi*
bi  1
S bi
sample size
 t / 2,nk 1
IV. Coefficient of Multiple Determination (R2)
Formula
2
R
=
SSR
SST
or
SSE
1
SST
Adjusted R2 =
 n  1 
2 
R  1  
1  R 
 n  k  1 

2
V. Confidence Interval
bi  t 2,n  k 1  Sbi
Range of numbers believed to include
an unknown population parameter.
Multiple Regression Example
 Deciding where to locate a new retail store
is one of the most important decisions that a
manger can make.
The director of Blockbuster Video plans to
use a regression model to help select a
location for a new store. She decides to use
the annual gross revenue as a measure of
success (Y). She uses a sample of 50 stores.
Determinants of Success
(X1) = Number of people living within one mile of the
store
(X2) = Mean income of households within one
mile of the store
(X3) = Number of Competitors within one mile of the
store
(X4) = Rental price of a newly released movie
Output from Computer
Regression Line:
Y= -20297+6.44X1+7.27X2-6,709X3+15,969X4
ANOVAb
Model
1
Regress ion
Res idual
Total
Sum of
Squares
4.06E+10
2.84E+10
6.90E+10
df
4
45
49
Mean Square
1.015E+10
632008977.4
F
16.054
a. Predictors : (Constant), PRICE, PEOPLE, INCOME, COMPTORS
b. Dependent Variable: REVENUE
Sig.
.000 a
Multiple Regression Example
Conduct the following tests:
•Overall Model F test
•Test whether β2 = 0 (sb2 = 3.705)
•Test whether β3 = -5000 (sb3 = 3,818)
•What is the R2? the adjusted R2?
•Construct a 95% confidence interval for β4
(sb4 = 10,219)
Correlation
 Measures the strength of the
linear relationship between two
variables
 Ranges from -1 to 1
 Positive = direct relationship
r
S xy
SxS y
 1 to  1
 Negative = inverse relationship
 Near 0 = no strong linear
relationship
 Does NOT imply causality
Sxy  covariance of X and Y
Sx  standard deviation of X
Sy  standard deviation of Y
Illustrations of correlation
Y
r=-1
Y
X
Y
r=-.8
X
Y
r=0
r=1
X
Y
X
Y
r=0
X
r=.8
X
VI. Hypothesis Test on Correlation
 To test the significance of the linear
relationship between two random variables:
H0:  = 0 no linear relationship
H1:   0 linear relationship
 This is a t-test with (n-2) degrees of freedom:
t / 2, n  2 
r
1 r2
n2
VI. Hypothesis Test on Correlation (cont.)
 Is the number of penalty flags thrown
by Big Ten Officials linearly related to
the number of points scored by the
football team? (n=100)
Sxy = - 59
Sx = 7.45
Sy = 9.10