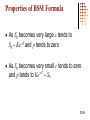Download Valuing Stock Options: The Black

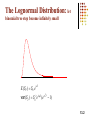
Valuing Stock Options :
The Black-Scholes-Merton
Model
Chapter 13
13.1
The Lognormal Distribution: let
binomial tree step become infinitely small
E ( ST )  S0 e T
2 2 T
var ( ST )  S0 e
(e
2T
 1)
13.2
The Volatility


The volatility is the standard deviation
of the continuously compounded rate
of return in 1 year
The standard deviation of the return in
time Dt is  Dt
13.3
Nature of Volatility


Volatility is usually much greater when the
market is open (i.e. the asset is trading)
than when it is closed
For this reason time is usually measured
in “trading days” not calendar days when
options are valued
13.4
The Concepts Underlying BSM





The option price and the stock price depend
on the same underlying source of uncertainty
We can form a portfolio consisting of the
stock and the option which eliminates this
source of uncertainty
If short 1 option, must be long delta share
If long 1 option, must be short delta share
The portfolio is instantaneously riskless and
must instantaneously earn the risk-free rate
13.5
The BSM Formulas (for European
options on nondividend paying shares)
c  S 0 N (d1 )  K e
 rT
N (d 2 )
p  K e  rT N (d 2 )  S 0 N (d1 )
2
ln( S 0 / K )  (r   / 2)T
where d1 
 T
ln( S 0 / K )  (r   2 / 2)T
d2 
 d1   T
 T
13.6
Delta and RNPE (risk neutral probability
of exercise)




Call delta = N(d1)
Call RNPE = N(d2)
Put delta = - N(- d1)
Put RNPE = N(- d2)
The N(x) Function: cumulative probability
distribution of the standardized normal random
variable



N(x) is the probability that a normally
distributed variable with a mean of zero
and a standard deviation of 1 is less than x
Tables in the book or Excel NormDist
function, but this not required in exam
Questions will require that you determine
the numerical value of d, say 1.2034, and
then provide answer as N(1.2034)
13.8
Properties of BSM Formula

As S0 becomes very large c tends to
S0 – Ke-rT and p tends to zero

As S0 becomes very small c tends to zero
and p tends to Ke-rT – S0
13.9
Risk-Neutral Valuation



The variable  does not appear in the BlackScholes equation
The equation is independent of all variables
affected by risk preference
This is consistent with the risk-neutral
valuation principle
13.10
Applying Risk-Neutral Valuation
1. Assume that the expected
return from an asset is the
risk-free rate
2. Calculate the expected payoff
from the derivative
3. Discount at the risk-free rate
13.11
Valuing a Long Forward Contract
with Risk-Neutral Valuation
K = contractual rate



Payoff is ST – K
Expected payoff in a risk-neutral world is
S0erT – K
Present value of expected payoff is
e-rT[S0erT – K]=S0 – Ke-rT
13.12
Implied Volatility



The implied volatility of an option is the
volatility for which the Black-ScholesMerton price equals the market price
The is a one-to-one correspondence
between prices and implied volatilities
Traders and brokers often quote implied
volatilities rather than dollar prices
13.13
Dividends



European options on dividend-paying
stocks: valued by substituting the stock
price less the present value of dividends
into the BSM formula (D vs. q)
Only dividends with ex-dividend dates
during life of option should be included
The “dividend” should be the expected
reduction in the stock price expected
13.14
American Calls


An American call on a non-dividend-paying
stock should never be exercised early
An American call on a dividend-paying stock
should only ever be exercised immediately
prior to an ex-dividend date
13.15
Black’s Approximation for Dealing with
Dividends in American Call Options
Set the American price equal to the
maximum of two European prices:
1. The 1st European price is for an
option maturing at the same time as the
American option
2. The 2nd European price is for an
option maturing just before the final exdividend date
13.16