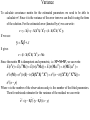Download Basic principles of probability theory

Basics of regression analysis I
•
•
•
Purpose of linear models
Least-squares solution for linear models
Analysis of diagnostics
Reason for linear models
Purpose of regression is to reveal statistical relations between input and output variables.
Statistics cannot reveal functional relationship. It is purpose of other scientific studies. Statistics
can help validation of various functional relationship (models). Let us assume that we suspect
that functional relationship has a form:
y  f (x,,)
where  is a vector of unknown parameters, x=(x1,x2,,,xp) a vector of controllable parameters, and
y is output,  is an error associated with the experiment. Then we can set up experiments for
various values of x and get output (or response) for them. If the number of experiments is n then

we will have n output values.
Denote them as a vector y=(y1,y2,,,yn). Purpose of statistics is to
evaluate parameter vector using input and output values. If function f is a linear function of the
parameters and errors are additive then we are dealing with linear model. For this model we can
write
yi  1 x1i   2 x2i  ...   p x pi   i
Linear model is linearly dependent on parameters but not on input variables. For example
y   0  1 x1   2 x12  
is a linear model. But
y   0  1 x1  12 x2  
is not.
Assumptions
Basic assumptions for analysis of linear model are:
1)
the model is linear in parameters
2)
the error structure is additive
3)
Random errors have 0 mean, equal variances and they are uncorrelated.
These assumptions are sufficient to deal with linear models. Uncorrelated with equal
variance assumptions (number 3) can be removed. Then the treatments
becomes a little bit more complicated.
Note that for general solution, normal distribution of errors assumption is not used.
This assumption is necessary to design test statistics. If this assumption breaks
down then we can use bootstrap or other approximate techniques to design test
statistic.
These assumptions can be written in a vector form:
y  X  , E( )  0, V()   2I
where y, 0,  are vectors and I and X are matrices. The matrix X is called a design
matrix, input matrix etc. I is nxn identity matrix.

One parameter case
When we have one variable (x) for predictor and one for response then problem
becomes considerable simpler. In this case we have:
y  0  1x  
Now let us assume that we have observations for n values of x (x1,,,xn). The response
vector is (y1,,,yn). If we assume that errors are independent, have equal variances
and normally
then maximum likelihood becomes least-square:
 distributed
n
n
   (y
2
i
i1
i
 ( 0  1 x i )) 2 - > min
i=1
If we solve this minimisation problem we get for estimations for coefficients:
y i  x i2   x i  y i x i

ˆ
0 
n x i2  ( x i ) 2

ˆ 

1

n y i x i   y i  x i
n x i2  ( x i ) 2
One parameter case
If you divide denominator and numerator by n2 and use definitions of correlation and
standard deviations then the second equation can be written as:
ˆ   (x, y)

1
s(y)
s(x)
Slope of the line is correlation between input and output variables.
If slope is
equal 0 (i.e. input and output variables are uncorrelated) then intercept
becomes mean value of the observations
Solution for the general case
Solution to the least-squares with linear model and and with given assumptions is:
ˆ  (XT X)1 XT y

Let us show this. If we use the form of the model and write least squares equation (since we want
to find solution with minimum least-squares error):
S  T  (y  X ) T (y  X )  min
and get the first and solve the equation then we can see that this solution is correct.

S
 2(XT X  XT y)  0


ˆ  (XT X)1 XT y

If we use the formula for the solution and the expression of y then we can write:
T
1 T
T
1 T
T
1 T
T
1 T
ˆ
E(
)  E((X X) X y)  E((X X) X (X  ))  E((X X) X X  (X X) X )
 E( )  (XT X)1 XT E()  
So solution is unbiased. Variance of the estimation is:
ˆ )  E((
ˆ  )(
ˆ  )T )  E((XT X)1 XTT X(XT X)1)  (XT X)1 XT E(T )X(XT X)1   2 (XT X)1
V(
Here we used the form of the solution and the assumption number 3)
Variance
To calculate covariance matrix for the estimated parameters we need to be able to
calculate 2. Since it is the variance of the error term we can find it using the form
of the solution. For the estimated error (denoted by r) we can write:
ˆ  y  X(XT X)1 XT y  (I  X(XT X)1 XT )y
r  y  X
If we use:
It gives

y  X  
r  (I  X(XT X)1 XT )  M
Since the matrix M is idempotent and symmetric, i.e. M2=M=MT, we can write:
 E(r T r)  E( T M)  E(tr( T M))  E(tr(M T )  tr(ME( T ) 
2 
 tr(M)   2 (tr(I)  tr(X(X T X) 1 XT )   2 (n  tr((XT X) 1 XT X)) 
 2 (n  p)
Where n is the number of the observations and p is the number of the fitted parameters.
Then for unbiased estimator for the variance of the residual we can write:
ˆ )T (y  X
ˆ ) /(n  p)
ˆ 2  (y  X

Singular case: SVD and psuedoinversion
The above form of the solution is true if matrices X and XTX are non-singular. I.e. the rank of
the matrix X is equal to the number of parameters. If it is not true then either singular
value decomposition or eignevalue filtering techniques are used. Fortunately most good
properties of the linear model remains.
Singular value decomposition (SVD): Any nxp matrix can be decomposed in a form:
X  UDV
Where U is nxn and V is pxp orthogonal matrices (inverse is equal to transpose). D is nxp
diagonal matrix of the singular values. If X is singular then number of non-zero diagonal
elements of D is less than p. Then for XTX we can write:
X TX  (UDV)T UDV  VTDTUTUDV  VTDTDV
DTD is pxp diagonal matrix. If the matrix is non-singular then we can write:
(X TX)1  VT (DTD)1 V
Since DTD is a diagonal matrix therefore its inverse is also diagonal matrix. Main trick used in
SVD technique for equation solution is that when diagonals are 0 or close to 0 then
instead of their inversion zero is used. I.e. pseudo inverse is calculated using:
(DD)
1*
ii

0
if correspond ing diagonal of DTD is 0

T
otherwise
1/( D D)ii
Singular case: Ridge regression
Another technique to deal with singular case is ridge regression. In this technique a
constant value added to the diagonal terms XTX before inverting it.
ˆ  (XT X I)1 XT y

Mathematically it is equivalent to Tikhonov regularisation for ill-posed problems.
In this technique
one of the problems is how to find the regularisation parameter - .

A value for this parameter can be found using cross validation. That is usually
done by trial and error.
Standard diagnostics
Before starting to model
1)
Visualisation of the data:
1)
2)
plotting predictor vs observations. These plots may give a clue about the relationship,
outliers
Smootheners
After modelling and fitting
2)
Fitted values vs residuals. It may help to identify outliers, correctness of the
model
3)
Normal QQ plot of residuals. It may help to check distribution assumptions
4)
Cook’s distance, reveals outliers, checks correctness of the model
5)
Model assumptions - t tests given by the default print of lm
Checking model and designing tests
3)
Cross-validation. If you have a choice of models then cross-validation may help
to choose the “best” model
4)
Bootstrap. Validity of the model can be checked if the distribution of statistic of
interest is available. Or these distributions could be generated using bootstrap
Visualisation prior to modelling
Different type of datasets may require different visualisation tools. For simple
visualisation either plot(data) or pairs(data,panel=panel.smooth) could be used.
Visualisation prior to modelling may help to propose a model (form of the functional
relationship between input and output, probability distribution of observation etc)
For example for dataset women - where weights and heights for 15 cases have been
measured. plot and pairs commands produce these plots:
After modelling: linear models
After modelling the results should be analysed. For example
attach(women)
lm1 = lm(weight~height)
It means that we want a liner model (we believe that dependence of weight on height is
linear):
weight=0+1*height
Results could be viewed using
lm1
summary(lm1)
The last command will produce significance of various coefficients also. Significance
levels produced by summary should be considered carefully. If there are many
coefficients then the chance that one “significant” effect is observed is very high.
After modelling: linear models
It is a good idea to plot data and fitted model, and differences between fitted and
observed values on the same graph. For linear models with one predictor it can be
done using:
plot(weight,height)
abline(lm1)
segements(weight,fitted(lm1),weight,height)
This plot already shows some systematic
differences. It is an indication that model
may need to be revised.
Checking validity of the model: standard tools
Plotting fitted values vs residual, QQ plot and Cook’s distance can give some insight
into model and how to improve it. Some of these plots can be done using
plot(lm1)
Confidence and prediction bands
Confidence bands are those where true line would belong with 1-α probability
ˆ, x)  c (x)  f (, x)  f (
ˆ, x)  c (x)) 1 
P( f (
1
1
Prediction bands are bands where future observation would full with probability of 1-α:

ˆ, x)  c (x)  y
ˆ, x)  c (x))  1 
P( f (
2
future  f (
2
Prediction bands are wider than confidence bands.

Prediction and confidence bands
lm1 = lm(height~weight)
pp = predict(lm1,interval='p')
pc = predict(lm1,interval='c')
plot(weight,height,ylim=range(height,pp))
n1=order(weight)
matlines(weight[n1],pp[n1,],lty=c(1,2,2),col='red')
matlines(weight[n1],pc[n1,],lty=c(1,3,3),col='red’)
These commands produce two sets
of bands: narrow and wide.
Narrow band corresponds to
confidence bands and wide band is
prediction band
Bootstrap
Simplest application of bootstrap for this problem is as follows:
1)
Calculate residuals using
ˆ
r  y  X
2)
3)
Sample with replacement from the residual vector and denote them rrandom
Design new “observations” using

4)
5)
6)
ˆ r
y  X
random
Estimate parameters
Repeat steps 2 3 and 4
Estimate bootstrap
 estimation, variances, covariance matrix or the
distribution
Another technique for bootstrapping is: Resample observations and corresponding
row of the design matrix simultaneously - (yi,x1i,x2i,,,,xpi),i=1,n. It meant to
be less sensitive to misspecified models.
Note that for some samples, the matrix may become singular and problem may
become ill defined. If it happens then ridge regression or similar techniques
need to be used
Bootstrap prediction lines
Bootstrap could be used to plot distribution of fitted model. This function is on:
http://www.ysbl.york.ac.uk/~garib/mres_course/2008/boot_lm_lines.r
If we apply this function for the dataset women we will get the lines shown on the figure
below.
boot_lm(women,flm0,1000)
Functions boot_lm and flm0 are available from the course’s website
Analysis of diagnostics
Residuals and hat matrix: Residuals are differences between observation and fitted
values:
ˆ  y  X(XT X) 1 XT y  (I  X(XT X) 1 XT )y  (I  H)y
r  y  yˆ  y  X
H is called a hat matrix. Diagonal terms hi are leverage of the observations. If these
values are close to one then that fitted value is determined by this observation.
Sometimes hi’=hi/(1-hi) is used to enhance high leverages.
Q-Q plot can be used to check normality assumption. If assumption on distribution is
correct then this plot should be nearly linear. If the distribution is normal then tests
designed for normal distributions can be used. Otherwise bootstrap may be more
useful to derive the desired distributions.
Analysis of diagnostics: Cont.
Other analysis tools include:
ri'  ri /( s(1  hi )1 / 2 ) standardiz ed (stutendiz ed) residual
ri*  ri /( si (1  hi )1 / 2 ) externally standardiz ed residual
Ci  ( hi ' )1 / 2 ri*
DFFITS
Where hi is leverage, hi’ is enhanced leverage, s2 is unbiased estimator of 2, si2 is
unbiased estimator of 2 after removal of i-th observation
R-squared
One of the statistics used for goodness of fit is R-squared. It is defined as:
SSe
SSt
SSe   (y i  yˆ i ) 2
R 2  1
SSt   (y i  y ) 2
yˆ i is fitted values.
Adjusted R-squared:

2
Radj
 1 (1 R 2 )
n 1
n  p 1
n - the number of observations, p - the number of parameters

Several potential problems with linear model and
simple regression analysis
1) Interpretation
Regression analysis can tell us that there is a relationship between input and output. It does not
say one causes another
2) Outliers
Use robust M-estimators
3) Singular or near singular cases
Ridge regression or SVD.
In underdetermined systems Partial least squares may be helpful
4) Distribution assumptions
Generalised linear models
Random or mixed effect models
Data transformation
5) Non-linear model
Box-Cox transformation
Non-linear model fitting for example using R command nlm
References
1.
2.
3.
Berthold, M. and Hand, DJ (2003) “Intelligent data analysis”
Stuart, A., Ord, JK, and Arnold, S. (1991) “Kendall’s advanced Theory of
statistics. Volume 2A. Classical Inference and the Linear models” Arnold
publisher, London, Sydney, Auckland
Dalgaard, P (2002) “Introductory statistics with R”, Springer Publishers