* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download DEB theory
Perceptual control theory wikipedia , lookup
Vector generalized linear model wikipedia , lookup
Inverse problem wikipedia , lookup
Predictive analytics wikipedia , lookup
Numerical weather prediction wikipedia , lookup
Theoretical ecology wikipedia , lookup
Regression analysis wikipedia , lookup
General circulation model wikipedia , lookup
History of numerical weather prediction wikipedia , lookup
Expectation–maximization algorithm wikipedia , lookup
Data assimilation wikipedia , lookup
Operational transformation wikipedia , lookup
Generalized linear model wikipedia , lookup
Least squares wikipedia , lookup
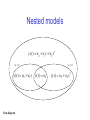
Art of modelling DEB course 2013 Bas Kooijman Dept theoretical biology Vrije Universiteit Amsterdam [email protected] http://www.bio.vu.nl/thb Texel, 2013/04/16 Modelling 1 • model: scientific statement in mathematical language “all models are wrong, some are useful” • aims: structuring thought; the single most useful property of models: “a model is not more than you put into it” how do factors interact? (machanisms/consequences) design of experiments, interpretation of results inter-, extra-polation (prediction) decision/management (risk analysis) Modelling 2 • language errors: mathematical, dimensions, conservation laws • properties: generic (with respect to application) realistic (precision) simple (math. analysis, aid in thinking) plasticity in parameters (support, testability) • ideals: assumptions for mechanisms (coherence, consistency) distinction action variables/meausered quantities core/auxiliary theory Causation Cause and effect sequences can work in chains AB C But are problematic in networks A B C Framework of dynamic systems allow for holistic approach Dynamic systems Defined by simultaneous behaviour of input, state variable, output Supply systems: input + state variables output Demand systems input state variables + output Real systems: mixtures between supply & demand systems Constraints: mass, energy balance equations State variables: span a state space behaviour: usually set of ode’s with parameters Trajectory: map of behaviour state vars in state space Parameters: constant, functions of time, functions of modifying variables compound parameters: functions of parameters Empirical cycle Modelling criteria • Consistency dimensions, conservation laws, realism (consistency with data) • Coherence consistency with neighbouring fields of interest, levels of organisation • Efficiency comparable level of detail, all vars and pars are effective numerical behaviour • Testability amount of support, hidden variables Dimension rules • quantities left and right of = must have equal dimensions • + and – only defined for quantities with same dimension • ratio’s of variables with similar dimensions are only dimensionless if addition of these variables has a meaning within the model context • never apply transcendental functions to quantities with a dimension log, exp, sin, … What about pH, and pH1 – pH2? • don’t replace parameters by their values in model representations y(x) = a x + b, with a = 0.2 M-1, b = 5 y(x) = 0.2 x + 5 What dimensions have y and x? Distinguish dimensions and units! Model without dimension problem Alternative form: k = k0 exp{1 – T0 /T}, with k0 = exp{a – 1} ln rate Arrhenius model: ln k = a – T0 /T k: some rate T: absolute temperature a: parameter T0: Arrhenius temperature Arrhenius plot Difference with allometric model: no reference value required to solve dimension problem T-1 Models with dimension problems 1.2.3 • Allometric model: y = a W b y: some quantity a: proportionality constant W: body weight b: allometric parameter in (2/3, 1) Usual form ln y = ln a + b ln W Alternative form: y = y0 (W/W0 )b, with y0 = a W0b Alternative model: y = a L2 + b L3, where L W1/3 • Freundlich’s model: C = k c1/n C: density of compound in soil k: proportionality constant c: concentration in liquid n: parameter in (1.4, 5) Alternative form: C = C0 (c/c0 )1/n, with C0 = kc01/n Alternative model: C = 2C0 c(c0+c)-1 (Langmuir’s model) Problem: No natural reference values W0 , c0 Values of y0 , C0 depend on the arbitrary choice Allometric functions O2 consumption, μl/h Two curves fitted: a L2 + b L3 with a = 0.0336 μl h-1 mm-2 b = 0.01845 μl h-1 mm-3 a Lb with a = 0.0156 μl h-1 mm-2.437 b = 2.437 Length, mm Kleber’s law O2 consumption weight3/4 O2 consumption has contributions from • maintenance & development • overheads of assimilation, growth & reproduction These are all functions of weight that should be added But: sum of functions of weight allometric function of weight Problem in relating respiration to other activities Egg development time D exp( 3.3956 0.2193 ln( T ) 0.3414(ln( T )) 2 ) D exp( a b ln( T ) c(ln( T )) 2 ) dim( a) ln t ln t dim( b) ln K ln t dim( c) (ln K ) 2 D egg developmen t time T temperatur e in Kelvin Bottrell, H. H., Duncan, A., Gliwicz, Z. M. , Grygierek, E., Herzig, A., Hillbricht-Ilkowska, A., Kurasawa, H. Larsson, P., Weglenska, T. 1976 A review of some problems in zooplankton production studies. Norw. J. Zool. 24: 419-456 Space-time scales space Each process has its characteristic domain of space-time scales system earth ecosystem population individual cell molecule When changing the space-time scale, new processes will become important other will become less important Individuals are special because of straightforward energy/mass balances time Complex models • hardly contribute to insight • hardly allow parameter estimation • hardly allow falsification Avoid complexity by • delineating modules • linking modules in simple ways • estimate parameters of modules only Biodegradation of compounds n-th order model d X kX n dt (1 n ) 1 1 n X (t ) X 0 (1 n)kt n 0 X (t ) X 0 kt ; t X 0 / k n 1 X (t ) X 0 exp{ kt} 1 n 1 a t (aX 0 ) X 01n k 1 1 n Monod model d X X k dt KX 0 X (t ) X 0 K ln{ X (t ) / X 0 } kt K X 0 X (t ) X 0 kt ; t X 0 exp{kt / K} K X 0 X (t ) X 0 exp{kt / K} 1 1 t (aX 0 ) X 0 k (a 1) Kk ln a X : conc. of compound, t : time n : order X0 : X at time 0 k : degradation rate K : saturation constant Biodegradation of compounds Monod model scaled conc. scaled conc. n-th order model scaled time scaled time Plasticity in parameters If plasticity of shapes of y(x|a) is large as function of a: • little problems in estimating value of a from {xi,yi}i (small confidence intervals) • little support from data for underlying assumptions (if data were different: other parameter value results, but still a good fit, so no rejection of assumption) Stochastic vs deterministic models Only stochastic models can be tested against experimental data Standard way to extend deterministic model to stochastic one: regression model: y(x| a,b,..) = f(x|a,b,..) + e, with e N(0,2) Originates from physics, where e stands for measurement error Problem: deviations from model are frequently not measurement errors Alternatives: • deterministic systems with stochastic inputs • differences in parameter values between individuals Problem: parameter estimation methods become very complex Statistics Deals with • estimation of parameter values, and confidence in these values • tests of hypothesis about parameter values differs a parameter value from a known value? differ parameter values between two samples? Deals NOT with • does model 1 fit better than model 2 if model 1 is not a special case of model 2 Statistical methods assume that the model is given (Non-parametric methods only use some properties of the given model, rather than its full specification) Large scatter • complicates parameter estimation • complicates falsification Avoid large scatter by • Standardization of factors that contribute to measurements • Stratified sampling Kinds of statistics 1.2.4 Descriptive statistics sometimes useful, frequently boring Mathematical statistics beautiful mathematical construct rarely applicable due to assumptions to keep it simple Scientific statistics still in its childhood due to research workers being specialised upcoming thanks to increase of computational power (Monte Carlo studies) Nested models y ( x) w0 w1 x w2 x 2 w2 0 y( x) w0 w1 x Venn diagram w1 0 y( x) w0 y ( x) w0 w2 x 2 Testing of hypothesis Error of the first kind: reject null hypothesis while it is true Error of the second kind: accept null hypothesis while the alternative hypothesis is true Level of significance of a statistical test: = probability on error of the first kind Power of a statistical test: = 1 – probability on error of the second kind No certainty in statistics decision null hypothesis true false accept 1- reject 1- Statements to remember • “proving” something statistically is absurd • if you do not know the power of your test, do don’t know what you are doing while testing • you need to specify the alternative hypothesis to know the power this involves knowledge about the subject (biology, chemistry, ..) • parameters only have a meaning if the model is “true” this involves knowledge about the subject Independent observations If X and Y are independent I I f Central limit theorems The sum of n independent identically (i.i.) distributed random variables becomes normally distributed for increasing n. Z X Y f Z ( z ) f X ( z y) fY ( y) dy; P( Z z ) P( X z y) P(Y y) y y The sum of n independent point processes tends to behave as a Poisson process for increasing n. Number of events in a time interval is i.i. Poisson distributed Time intervals between subsequent events is i.i. exponentially distributed Poisson prob Exponential prob dens Sums of random variables n Y Xi; i 1 Var (Y ) nVar ( X i ) f X ( x) λ exp( λx) λ fY ( y ) (λy) n1 exp( λy ) ( n) λx P( X x) exp( λ) x! (nλ) y P(Y y ) exp( nλ) y! Normal probability density σ σ 95% (x-μ)/σ 1 x μ 2 f X ( x) exp 2 2πσ 2 σ 1 f X ( x) 1 exp x μ ' -1 x μ 2π n 2 1 Parameter estimation Most frequently used method: Maximization of (log) Likelihood likelihood: probability of finding observed data (given the model), considered as function of parameter values If we repeat the collection of data many times (same conditions, same number of data) the resulting ML estimate Profile likelihood large sample approximation 95% conf interval Comparison of models Akaike Information Criterion for sample size n and K parameters n 2 log L(θ) 2 K n K 1 in the case of a regression model n 2 n log σ 2 K n K 1 You can compare goodness of fit of different models to the same data but statistics will not help you to choose between the models Confidence intervals length, mm L(t ) L ( L L0 ) exp( rB t ) L0 ( L L0 )rB t for small t L0 1 excludes point 4 95% conf intervals rB includes point 4 time, d L correlations among parameter estimates can have big effects on sim conf intervals estimate excluding point 4 sd excluding point 4 estimate including point 4 sd including point 4 L, mm 6.46 1.08 3.37 0.096 rB,d-1 0.099 0.022 0.277 0.023 parameter :No age, but size:These gouramis are from the same nest, they have the same age and lived in the same tank Social interaction during feeding caused the huge size difference Age-based models for growth are bound to fail; growth depends on food intake Trichopsis vittatus Rules for feeding determin expectation length reserve density Social interaction Feeding time time 1 ind 2 ind length reserve density time time Dependent observations Conclusion Dependences can work out in complex ways The two growth curves look like von Bertalanffy curves with very different parameters But in reality both individuals had the same parameters!