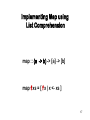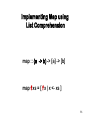Download document

COMP313A
Functional Programming (1)
1
Main Differences with Imperative
Languages
• Say more about what is computed as
opposed to how
• Pure functional languages have no
– variables
– assignments
– other side effects
• Means no loops
2
Differences…
• Imperative languages have an implicit
state (state of variables) that is modified
(side effect).
• Sequencing is important to gain precise,
deterministic control over the state
• assignment statement needed to change
the binding for a particular variable (alter
the implicit state)
3
• Imperative factorial
n:=x;
a:=1;
while n > 0 do
begin
a:= a * n;
n := n-1;
end;
4
Differences
• Declarative languages have no implicit
state
• Program with expressions
• The state is carried around explicitly
– e.g. the formal parameter n in factorial
• Looping is accomplished with recursion
rather than sequencing
5
Haskell
fac ::Int -> Int
fac n
| n == 0 = 1
| n > 0 = fac(n-1) * n
| otherwise = 0
Scheme
(define fac
(lambda (n)
(if (= n 0)
1
(* n (fac (- n 1))))))
6
Advantages
• similar to traditional mathematics
• referential transparency makes programs
more readable
• higher order functions give great
flexibility
• concise programs
7
Referential Transparency
• the value of a function depends only on
the values of its parameters
for example Haskell
…x + x…
where x = f a
8
Evolution of Functional languages
Lambda Calculus
• Alonzo Church
• Captures the essence of functional
programming
• Formalism for expressing computation by
functions
• Lambda abstraction
(lx. + 1 x)
• In Scheme
• In Haskell
(lambda(x) (+ 1 x)))
add1 :: Int -> Int
add1 x
=1+x
9
Lambda Calculus…
• application of expressions
(lx. + 1 x) 2
• reduction rule that substitutes 2 for x in
the lambda (beta reduction)
(lx. + 1 x) 2  (+ 1 2)  3
(lx. * x x) (+ 2 3)
i.e. (+ 2 3) / x)
10
Lambda Calculus…
• (lx.E)
– variable x is bound by the lambda
– the scope of the binding is the expression E
• (lx. + y x)
– (lx. + y x)2  (+ y 2)
• (lx. + ((ly. ((lx. * x y) 2)) x) y) 
11
Lambda Calculus…
• Each lambda abstraction binds only one
variable
• Need to bind each variable with its own
lambda.
(lx. (ly. + x y))
12
Lisp
• McCarthy late 1950s
• Used Lambda Calculus for
anonymous functions
• List processing language
• First attempt built on top of
FORTRAN
13
LISP…
•
McCarthy’s main contributions were
1. the conditional expression and its use in
writing recursive functions
Scheme
(define fac
(lambda (n)
(if (= n 0)
1
(if (> n 0) (* n (fac (- n 1)))
0))))
Haskell
fac :: Int -> Int
fac n
= if n == 0 then 1
else if n > 0 then fac(n-1) * n
else 0
Scheme
(define fac2
(lambda (n)
(cond ((= n 0) 1)
((> n 0) (* n (fac2 (- n 1))))
(else 0))))
Haskell
fac ::Int -> Int
fac n
| n == 0 = 1
| n > 0 = fac(n-1) * n
| otherwise = 0
14
Lisp…
2.the use of lists and higher order operations
over lists such as mapcar
Scheme
(define mymap
(lambda (f a b)
(cond ((and (null? a) (null? b)) '())
(else (cons (f (first a) (first b))
(mymap f (rest a) (rest b)))))))
Haskell
mymap :: (Int -> Int-> Int) -> [Int] -> [Int] ->[Int]Scheme
(mymap + ’(3 4 6) ’(5 7 8))
mymap f [] [] = []
mymap f (x:xs) (y:ys) = f x y : mymap f xs ys
Haskell
mymap add [3, 4, 6] [5, 7, 8]
add :: Int -> Int -> Int
15
add x y = x + y
Lisp
3. cons cell and garbage collection of
unused cons cells
Scheme
(cons ’1 ’(3 4 5 7))
(1 3 4 5 7)
Haskell
cons :: Int -> [Int] ->
[Int]
cons x xs = x:xs
Scheme
(define mymap
(lambda (f a b)
(cond ((and (null? a) (null? b)) '())
(else (cons (f (first a) (first b))
(mymap f (first a) (first b)))))))
16
Lisp…
4. use of S-expressions to represent both
program and data
An expression is an atom or a list
But a list can hold anything…
17
Scheme
(cons ’1 ’(3 4 5 7))
(1 3 4 5 7)
Scheme
(define mymap
(lambda (f a b)
(cond ((and (null? a) (null? b)) '())
(else (cons (f (first a) (first b))
(mymap f (first a) (first b)))))))
18
ISWIM
• Peter Landin – mid 1960s
• If You See What I Mean
Landon wrote “…can be looked upon as
an attempt to deliver Lisp from its
eponymous commitment to lists, its
reputation for hand-to-mouth storage
allocation, the hardware dependent
flavour of its pedagogy, its heavy
bracketing, and its compromises with
tradition”
19
Iswim…
• Contributions
– Infix syntax
– let and where clauses, including a notion of
simultaneous and mutually recursive
definitions
– the off side rule based on indentation
• layout used to specify beginning and end of
definitions
– Emphasis on generality
• small but expressive core language
20
let in Scheme
• let* - the bindings are performed
sequentially
(let* ((x 2)
(y 3)) 
(* x y))
(let* ((x 2) (y 3))
(let* ((x 7)
(z (+ x y)))
(* z x)))

21
let in Scheme
• let - the bindings are performed in parallel, i.e.
the initial values are computed before any of the
variables are bound
(let ((x 2) (y 3))  ?
(* x y))
(let ((x 2) (y 3))
(let ((x 7)
(z (+ x y))) 
(* z x)))
?
22
letrec in Scheme
• letrec – all the bindings are in effect while
their initial values are being computed,
allows mutually recursive definitions
(letrec ((even?
(lambda (n)
(if (zero? n)
#t
(odd? (- n 1)))))
(odd?
(lambda (n)
(if (zero? n)
#f
(even? (- n 1))))))
(even? 88))
23
ML
• Gordon et al 1979
• Served as the command language for a proof
generating system called LCF
– LCF reasoned about recursive functions
• Comprised a deductive calculus and an
interactive programming language – Meta
Language (ML)
• Has notion of references much like locations in
memory
• I/O – side effects
• But encourages functional style of programming24
ML
• Type System
– it is strongly and statically typed
– uses type inference to determine the type of
every expression
– allows polymorphic functions
• Has user defined ADTs
25
SASL, KRC, and Miranda
•
•
•
•
Used guards
Higher Order Functions
Lazy Evaluation
Currying
SASL
fac n = 1,
= n * fac (n-1),
Haskell
fac n
| n ==0
| n >0
n=0
n>0
=1
= n * ( fac(n-1)
add x y = + x y
add 1
switch :: Int -> a -> a -> a
switch n x y
|n>0
=x
| otherwise
=y
multiplyC :: Int -> Int -> Int
Versus
multiplyUC :: (Int, Int) -> Int
26
SASL, KRC and Miranda
• KRC introduced list comprehension
comprehension :: [Int] -> [Int]
comprehension ex
= [2 * n | n <- ex]
• Miranda borrowed strong data typing and
user defined ADTs from ML
27
COMP313A
Functional Programming (1)
28
LISP…
•
McCarthy’s main contributions were
1. the conditional expression and its use in
writing recursive functions
Scheme
(define fac
(lambda (n)
(if (= n 0)
1
(if (> n 0) (* n (fac (- n 1)))
0))))
Haskell
fac :: Int -> Int
fac n
= if n == 0 then 1
else if n > 0 then fac(n-1) * n
else 0
Scheme
(define fac2
(lambda (n)
(cond ((= n 0) 1)
((> n 0) (* n (fac2 (- n 1))))
(else 0))))
Haskell
fac ::Int -> Int
fac n
| n == 0 = 1
| n > 0 = fac(n-1) * n
| otherwise = 0
29
Lisp…
2.the use of lists and higher order operations
over lists such as mapcar
Scheme
(define mymap
(lambda (f a b)
(cond ((and (null? a) (null? b)) '())
(else (cons (f (first a) (first b))
(mymap f (rest a) (rest b)))))))
Haskell
mymap :: (Int -> Int-> Int) -> [Int] -> [Int] ->[Int]
mymap f [] [] = []
mymap f (x:xs) (y:ys) = f x y : mymap f xs ys
add :: Int -> Int -> Int
add x y = x + y
Scheme
(mymap + ’(3 4 6) ’(5 7 8))
Haskell
mymap add [3, 4, 6] [5, 7, 8]
30
Lisp
3. cons cell and garbage collection of
unused cons cells
Scheme
(cons ’1 ’(3 4 5 7))
(1 3 4 5 7)
Haskell
cons :: Int -> [Int] -> [Int]
cons x xs = x:xs
Scheme
(define mymap
(lambda (f a b)
(cond ((and (null? a) (null? b)) '())
(else (cons (f (first a) (first b))
(mymap f (first a) (first b)))))))
31
Lisp…
4. use of S-expressions to represent both
program and data
An expression is an atom or a list
But a list can hold anything…
32
Scheme
(cons ’1 ’(3 4 5 7))
(1 3 4 5 7)
Scheme
(define mymap
(lambda (f a b)
(cond ((and (null? a) (null? b)) '())
(else (cons (f (first a) (first b))
(mymap f (first a) (first b)))))))
33
ISWIM
• Peter Landin – mid 1960s
• If You See What I Mean
Landon wrote “…can be looked upon as
an attempt to deliver Lisp from its
eponymous commitment to lists, its
reputation for hand-to-mouth storage
allocation, the hardware dependent
flavour of its pedagogy, its heavy
bracketing, and its compromises with
tradition”
34
Iswim…
• Contributions
– Infix syntax
– let and where clauses, including a notion of
simultaneous and mutually recursive
definitions
– the off side rule based on indentation
• layout used to specify beginning and end of
definitions
– Emphasis on generality
• small but expressive core language
35
let in Scheme
• let* - the bindings are performed
sequentially
(let* ((x 2)
(y 3)) 
(* x y))
(let* ((x 2) (y 3))
(let* ((x 7)
(z (+ x y)))
(* z x)))

36
let in Scheme
• let - the bindings are performed in parallel, i.e.
the initial values are computed before any of the
variables are bound
(let ((x 2) (y 3))  ?
(* x y))
(let ((x 2) (y 3))
(let ((x 7)
(z (+ x y))) 
(* z x)))
?
37
letrec in Scheme
• letrec – all the bindings are in effect while
their initial values are being computed,
allows mutually recursive definitions
(letrec ((even?
(lambda (n)
(if (zero? n)
#t
(odd? (- n 1)))))
(odd?
(lambda (n)
(if (zero? n)
#f
(even? (- n 1))))))
(even? 88))
38
• Emacs was/is written in LISP
• Very popular in AI research
39
ML
• Gordon et al 1979
• Served as the command language for a proof
generating system called LCF
– LCF reasoned about recursive functions
• Comprised a deductive calculus and an
interactive programming language – Meta
Language (ML)
• Has notion of references much like locations in
memory
• I/O – side effects
• But encourages functional style of programming
40
ML
• Type System
– it is strongly and statically typed
– uses type inference to determine the type of
every expression
– allows polymorphic functions
• Has user defined ADTs
41
SASL, KRC, and Miranda
•
•
•
•
Used guards
Higher Order Functions
Lazy Evaluation
Currying
SASL
fac n = 1,
= n * fac (n-1),
Haskell
fac n
| n ==0
| n >0
n=0
n>0
=1
= n * fac(n-1)
add x y = + x y
silly_add x y = x
add 4 (3 * a)
switch :: Int -> a -> a -> a
switch n x y
|n>0
=x
| otherwise
=y
multiplyC :: Int -> Int -> Int
Versus
multiplyUC :: (Int, Int) -> Int
42
SASL, KRC and Miranda
• KRC introduced list comprehension
comp_example :: [Int] -> [Int]
comp_example ex = [2 * n | n <- ex]
• Miranda borrowed strong data typing and
user defined ADTs from ML
43
The Move to Haskell
• Lots of functional languages in late 1970’s
and 1980’s
• Tower of Babel
• Among these was Hope
– strongly typed
– polymorphism but explicit type declarations as
part of all function definitions
– simple module facility
– user-defined concrete data types with pattern
matching
44
The Move to Haskell
• 1987 – considered lack of common
language was hampering the adoption of
functional languages
• Haskell was born
–
–
–
–
–
–
higher order functions
lazy evaluation
static polymorphic typing
user-defined datatypes
pattern matching
list comprehensions
45
Haskell…
• as well
– module facility
– well defined I/O system
– rich set of primitive data types
46
Higher Order Functions
• Functions as first class values
– stored as data structures, passed as
arguments, returned as results
• Function is the primary abstraction
mechanism
– increase the use of this abstraction
• Higher order functions are the “guts” of
functional programming
47
Higher Order Functions
Computations over lists
• Mapping
– add 5 to every element of a list.
– add the corresponding elements of 2 lists
• Filtering
– Selecting the elements with a certain property
• Folding
– Combine the items in a list in some way
48
List Comprehension
Double all the elements in a list
Using primitive recursion
doubleAll :: [Int] -> [Int]
doubleAll [] = []
doubleAll x:xs = 2 * x : doubleAll xs
Using list comprehension
doubleAll :: [Int] -> [Int]
doubleAll xs :: [ 2 * x | x <- xs ]
49
Primitive Recursion
versus
General Recursion
sum :: [Int] -> Int
sum []
=0
sum (x:xs)
= x + sum xs
qsort :: [Int] -> [Int]
qsort [] = []
qsort (x : xs)
= qsort [ y | y<-xs , y<=x] ++ [x] ++ qsort [ y | y <- xs , y>x]
50
COMP313A
Functional Programming (3)
51
Higher Order Functions
• Functions as first class values
– stored as data structures, passed as
arguments, returned as results
• Function is the primary abstraction
mechanism
– increase the use of this abstraction
• Higher order functions are the “guts” of
functional programming
52
Higher Order Functions
Computations over lists
• Mapping
– add 5 to every element of a list.
– add the corresponding elements of 2 lists
• Filtering
– Selecting the elements with a certain property
• Folding
– Combine the items in a list in some way
53
List Comprehension
Double all the elements in a list
Using primitive recursion
doubleAll :: [Int] -> [Int]
doubleAll [] = []
doubleAll x:xs = 2 * x : doubleAll xs
Using list comprehension
doubleAll :: [Int] -> [Int]
doubleAll xs = [ 2 * x | x <- xs ]
54
Primitive Recursion
versus
General Recursion
sum :: [Int] -> Int
sum []
=0
sum (x:xs)
= x + sum xs
qsort :: [Int] -> [Int]
qsort [] = []
qsort (x : xs)
= qsort [ y | y<-xs , y<=x] ++ [x] ++ qsort [ y | y <- xs , y>x]
55
Some Haskell Syntax
Write a function to calculate the maximum of three numbers
i.e. maxThree :: Int -> Int -> Int
maxThree x y z
| x >= y && x >= z = x
| y >= z
=y
| otherwise
=z
56
Write a function to calculate the average of three numbers
averageThree :: Int-> Int -> Int -> Float
averageThree x y z
= (x + y + z) / 3
funny x = x + x
peculiar y = y
funny x = x + x
peculiar y = y
57
Tuples and Lists
Examples of lists
[345, 67, 34, 9]
[‘a’, ‘h’, ‘z’]
[“Fred”, “foo”]
Examples of tuples
(“Fred”, 471)
(“apples”, 3.41)
(“baseball_bat”, “aluminium” 60.0)
Strings are lists of char i.e. [Char]
[‘f’, ‘r’, ‘e’, ‘d’] = “fred”
58
Types
type album = (String, String, Int)
type collection = [album]
59
Some more examples
pattern matching
Write a function which will extract all the even numbers
from a list
Lets first create an isEven predicate
isEven n = (n ‘mod’ 2 == 0)
evenList [] = []
evenList ex = [n | n <- ex , isEven n]
evenList2 [] = []
evenList2 (x:xs)
|isEven x
= x : evenList2 xs
|otherwise
= evenList2 xs
60
Write a function listpairs which returns a list of the pairs
of corresponding elements in two lists
listpairs :: [a] -> [b] -> [(a,b)]
>>listpairs [3, 4, 5] [6, 7, 8]
>> [(3,6), (4, 7), (5,8)]
Would this work?
listpairs xs ys
= [(m,n) | m <- xs, n <- ys]
61
COMP313A
Functional Programming (4)
62
Lecture Outline
• A little bit of revision
• Higher Order Functions
– Functions as arguments
– Functions as values
63
Some more examples
pattern matching
Write a function which will extract all the even numbers
from a list
Lets first create an isEven predicate
isEven n = (mod n 2 == 0)
evenList [] = []
evenList ex = [n | n <- ex , isEven n]
evenList2 [] = []
evenList2 (x:xs)
|isEven x
= x : evenList2 xs
|otherwise
= evenList2 xs
64
List Comprehension
Given a function isDigit
isDigit :: Char -> Bool
which returns True if a character is a digit, write a function
digits which will find all the digits in a string
digits str
= [ aChar | aChar <-
,
]
65
Map
double x = 2 * x
doubleAll xs = map double xs
 doubleAll [4, 5, 6]
 [8, 10, 12]
66
Implementing Map using
List Comprehension
map :: (a -> b) -> [a] -> [b]
map f xs = [ f x | x <- xs ]
67
Functions as Arguments
fold
> foldr1 (+) [4, 5, 6]
> 15
68
foldr1 (non empty list)
foldr1 :: (a -> a -> a) -> [a] -> a
foldr1 f [x]
=x
foldr1 f (x:xs)
= f x (foldr f xs)
What does this tell us abut the characteristics of
function “f”
Produces an error when given an empty list
How could we define foldr to work with an empty list
69
foldr f s []
= s
foldr f s (x:xs) = f x (foldr f s xs)
70
1 More Higher Order Function
Filter
isEven n
= (mod n 2 == 0)
> filter isEven [2, 4, 6, 7, 1]
>??
isEven returns a predicate (returns a Bool)
71
Implementing Filter using
list comprehension
filter p xs = [x | x <- xs, p x]
p returns a Bool
72
Some exercises
•
Write functions to
(1) Return the list consisting of the squares
of the integers in a list, ns.
(2) Return the sum of squares of items in a
list
(3) Check whether all the items of a list are
greater than zero using filter
73
Functions as values
• functions as data
• function composition
sqr (succ 5)
concat (map bracketedWithoutVowels xs)
concatenates a list of lists into a single list
flattens a list
74
Functions as values
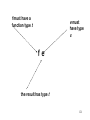
Function Composition (.)
(sqr . succ) 5
• The output of one function becomes the input of
another
a
f.g
a
g
b
f
c
c
(.) :: (b -> c) -> (a ->b) -> (a -> c)
type of f
type of g
type of (f.g)
75
f . g x as opposed to (f . g) x
Function application binds more
tightly than composition
e.g not . not True
or
succ .pred 5
76
Functions as values and results
twice fun = ( fun . fun )
• fun is a function
• The result is fun composed with itself
For this to work fun has to have …..
and twice :: (
) -> (
)
> twice succ 2
>4
77
Expressions Defining Functions
addnum :: Int -> (Int -> Int)
addnum n = addN
where
addN m = n + m
When addnum 10 say is called returns a function
addN which adds 10 to m
78
Main> addNum 4 5
9
Main> addNum 4
ERROR - Cannot find "show" function for:
*** Expression : addNum 4
*** Of type : Integer -> Integer
79
test :: Int -> Int -> Int
test x y
| x >= y = f y
| otherwise = 4
where
f = addnum 4
80
COMP313A
Functional Programming (4)
81
Lecture Outline
• A little bit of revision
• Higher Order Functions
– Functions as arguments
– Functions as values
82
Some more examples
pattern matching
Write a function which will extract all the even numbers
from a list
Lets first create an isEven predicate
isEven n = (mod n 2 == 0)
evenList [] = []
evenList ex = [n | n <- ex , isEven n]
evenList2 [] = []
evenList2 (x:xs)
|isEven x
= x : evenList2 xs
|otherwise
= evenList2 xs
83
List Comprehension
Given a function isDigit
isDigit :: Char -> Bool
which returns True if a character is a digit, write a function
digits which will find all the digits in a string
digits str
= [ aChar | aChar <-
,
]
84
Map
double x = 2 * x
doubleAll xs = map double xs
 doubleAll [4, 5, 6]
 [8, 10, 12]
85
Implementing Map using
List Comprehension
map :: (a -> b) -> [a] -> [b]
map f xs = [ f x | x <- xs ]
86
Functions as Arguments
fold
> foldr1 (+) [4, 5, 6]
> 15
87
foldr1 (non empty list)
foldr1 :: (a -> a -> a) -> [a] -> a
foldr1 f [x]
=x
foldr1 f (x:xs)
= f x (foldr f xs)
What does this tell us abut the characteristics of
function “f”
Produces an error when given an empty list
How could we define foldr to work with an empty list
88
foldr f s []
= s
foldr f s (x:xs) = f x (foldr f s xs)
89
1 More Higher Order Function
Filter
isEven n
= (mod n 2 == 0)
> filter isEven [2, 4, 6, 7, 1]
>??
isEven returns a predicate (returns a Bool)
90
Implementing Filter using
list comprehension
filter p xs = [x | x <- xs, p x]
p returns a Bool
91
Some exercises
•
Write functions to
(1) Return the list consisting of the squares
of the integers in a list, ns.
(2) Return the sum of squares of items in a
list
(3) Check whether all the items of a list are
greater than zero using filter
92
Functions as values
• functions as data
• function composition
sqr (succ 5)
concat (map bracketedWithoutVowels xs)
concatenates a list of lists into a single list
flattens a list
93
Functions as values
Function Composition (.)
(sqr . succ) 5
• The output of one function becomes the input of
another
a
f.g
a
g
b
f
c
c
(.) :: (b -> c) -> (a ->b) -> (a -> c)
type of f
type of g
type of (f.g)
94
f . g x as opposed to (f . g) x
Function application binds more
tightly than composition
e.g not . not True
or
succ .pred 5
95
Functions as values and results
twice fun = ( fun . fun )
• fun is a function
• The result is fun composed with itself
For this to work fun has to have …..
and twice :: (
) -> (
)
> twice succ 2
>4
96
Expressions Defining Functions
addnum :: Int -> (Int -> Int)
addnum n = addN
where
addN m = n + m
When addnum 10 say is called returns a function
addN which adds 10 to m
97
Main> addNum 4 5
9
Main> addNum 4
ERROR - Cannot find "show" function for:
*** Expression : addNum 4
*** Of type : Integer -> Integer
98
test :: Int -> Int -> Int
test x y
| x >= y = f y
| otherwise = 4
where
f = addnum 4
99
COMP313A Programming
Languages
Functional Programming (5)
100
Lecture Outline
• Higher order functions
• Functions as arguments
• Some recapping and
exercises
• Some more functions as data
and results
101
Expressions Defining Functions
addnum :: Int -> (Int -> Int)
addnum n = addN
where
-- local definition
addN m = n + m
When addnum 10 say is called returns a function
addN which adds 10 to m
102
test :: Int -> Int -> Int
test x y
| x >= y = somefun f y
| otherwise = 4
where
f = addnum 4
103
Lambda in Haskell
\m -> n + m
addNum n = (\m -> n + m)
Write a function “test n” that returns a function which tests
if some argument is <= to n. Use a lambda.
104
Partial Application of Functions
add :: Int -> Int -> Int
add x y = x+y
4
5
4
105
Partial Application of Functions…
add4 :: [Int] -> [Int]
add4 xs = map (add 4) xs
add4 :: ([Int] -> [Int])
add4 = map (add 4)
How would we use partial applications of functions to get the
same result as the “addNum n” example?
106
Types of partial applications
The type of function is
t1 -> t2 -> … tn -> t
and it is applied to arguments
e1 :: t1, e2 :: t2 … , ek :: tk
if k <= n (partial application) then cancel the
ones that match t1 – tk
leaving
tk+1 -> tk+2 -> … -> tn
107
Types of Partial Function Application
add :: Int -> Int -> Int
add 2
:: Int ->Int
add 2 3 :: Int
108
Operator Sections
(*2)
(2*)
(>2)
(6:)
(\2)
filter (>0) . map (+1)
Find operator sections sec1 and sec2 so that
map sec1. filter sec2
Has the same effect as filter (>0) . map (+1)
109
Partial Application of Functions
and
Operator Sections
elem :: Char -> [Char] -> Bool
elem ch whitespace
where whitespace is the string “ \t\n”
110
Partial Application of Functions
and Operator Sections
i.e. whitespace = “ \t\n”
The problem with partial application of function is that the argument
of interest may not always be the first argument
So
member xs x = elem x xs
and
member whitespace
Alternatively we can use a lambda function
\ch -> elem ch whitespace
111
Partial Application of Functions
and
Operator Sections
To filter all non-whitespace characters from
a string
filter (not . member whitespace)
filter (\ch -> not (elem ch whitespace))
112
Write a recursive function to extract a
word from a string
whitespace = “ \n\t”
getword :: String -> String
getword [ ] = [ ]
getword (x : xs)
|
--how do we know we have a word
|
-- otherwise build the word
- - recursively
getword “the quick brown”
113
Write a recursive function to extract a
word from a string
Can write something more general - pass the “test” as an
argument
getUntil :: (a -> Bool) -> [a] -> [a]
getUntil p [ ] = [ ]
getUntil p (x:xs)
|px
= []
| otherwise = x : getUntil p xs
114
Write a recursive function to extract a
word from a string
Okay but now how do we get a word
getWord xs
= getUntil p xs
where
- - local definition
p x = member whitespace x
115
Write a recursive function to extract a
word from a string
But we don’t really need the local definition
We can use our partial function instead
getWord xs
= getUntil p xs
where
- - local definition
p x = member whitespace x
getWord xs
= getUntil (member whitespace) xs
116
Write a recursive function to extract a
word from a string
Finally
The last word
getWord = getUntil (member whitespace)
---get characters until a whitespace is found
117
Currying and Uncurrying
• functions of two or more arguments take
arguments in sequence, one at a time.
– this is the curried form.
– named after Haskell Curry
• Uncurried version puts the arguments
into a pair
addUC :: (Int, Int) -> Int
addUC (x,y) = (x + y)
118
curried versus uncurried
• Curried has neater notation
• Curried permits partial application
• Can easily convert from one to the other
curry f (x y) = f x y
uncurry f x y = f (x y)
119
Type Checking in Haskell
Monomorphic Type Checking
• Expressions
literal, variable, constant, function applied to
some arguments
• type checking function application
– what do we need to consider
120
f must have a
e must
function type t
have type
s
fe
the result has type t
121
ord ‘c’ +Int 3Int
ord ‘c’ +Int False
122
Type Checking Function Definitions
fib :: Int ->Int
fib n
| n == 0
| n == 1
| n >1
=0
=1
= fib (n-2) + fib (n-1)
•Each of the guards must be of type ?
•The value returned in each clause must be of type ?
•The pattern n must be consistent with type argument ?
123
COMP313A Programming
Languages
Logic Programming (1)
124
Lecture Outline
• Conceptual foundations of Logic
Programming
• The Basics of Logic Programming
– Predicate Calculus
• A little bit of logic programming
– Prolog
125
Conceptual Foundations
• What versus how
– specification versus implementation
• Declarative Programming
– Programmer declares the logical properties that
describe the property to be solved
– From this a solution is inferred
– Inference engine
126
An example
Searching for an element in a list
Predicate is_in(x,L) true whenever element x is in the list L.
For all elements x and lists L: is_in(x,L) IFF
L = [x]
or
L = L1 . L2 and
(is_in (x,L1) or is_in(x, L2))
127
Example continued
Implementation
• Need to know how to split a list into right
and left sublists
• How to order the elements stored in the
list
128
A solution in C++
int binary_search(const int val, const int size, const int array[]){
int high, low, mid;
if size <= 0{
return (-1);
}
high = size;
low = 0;
for(;;) {
mid = (high + low) / 2;
if (mid = low){
return (val != array[low]) ?-1:mid;
}
if (val < array[mid]) {
high = mid;
}
else if (val > array[mid]) {
low = mid;
}
else return mid
}}}
129
A Declarative Solution
Given an element x and a list L, to prove that x is in L,
proceed as follows:
(1) Prove that L is [x]
(2) Otherwise split L into L1 . L2 and prove one of the following
(2.1) x is in L1, or
(2.2) x is in L2
130
A sorting example
A predicate sort(X,Y)
Sort(X,Y) is true if the nonempty list Y is the sorted
version of X
Use two auxiliary predicates: permutation(X,Y) and
is_sorted(Y)
For all integer lists X,Y: sort(X,Y) iff
permutation(X,Y) and sorted(Y)
131
Logic and Logic Programming
• First-order predicate calculus
– Logic statements
Examples
John is a man.
John is a human.
Tristan is the son of Margaret.
A horse is a mammal.
0 is a natural number .
man(John).
human(John).
son(Margaret,Tristan).
loathes(Margaret, Heavy_Metal).
natural(0).
Mammals have four legs and no arms or two legs and two arms.
For all X, mammal (x) -> legs(x,4) and arms(x,0) or legs(x,2) and
arms(x,2).
Humans have two legs and two arms.
For all X, human(x) -> legs(x,2) and arms(x,2).
If x is a natural number then so is the successor of x.
For all x, natural(x) -> natural(successor(x)).
132
First-Order Predicate Calculus
•
•
•
•
•
•
•
•
•
Constants
Predicates
Functions
Variables that stand for as yet unamed quantities
Atomic sentences
Connectives construct more complex sentences
Quantifiers
Punctuation
Arguments to predicates can only be terms –
variables, constants and functions
133
First-Order Predicate Calculus cont…
• Quanitifiers
– Universal, existential
• Express properties of entire collections of
objects
• Universal quantifiers make statements about
every object, "x
A cat is a mammal
"x Cat(x)  Mammal(x)
Cat(Spot)  Mammal(Spot) 
Cat(Rebecca)  Mammal(Rebecca) 
Cat(Felix)  Mammal(Felix) 
Cat(Richard)  Mammal(Richard) 
Cat(John)  Mammal(John) 
…
134
First-Order Predicate Calculus cont…
• Existential Quantifiers make statements about
some objects, $x
Spot has a sister who is a cat
$x Sister(x, Spot)  Cat(x)
(Sister(Spot, Spot)  Cat(Spot)) 
(Sister(Rebecca, Spot)  Cat(Rebecca)) 
(Sister(Felix, Spot)  Cat(Felix)) 
(Sister(Richard, Spot)  Cat(Richard)) 
(Sister(John, Spot)  Cat(John)) 
…
135
First-Order Predicate Calculus cont…
• Connections between $ and "
• Negation
Everyone dislikes rugby Noone likes rugby
"x Likes (x, rugby)  $x Likes(x, rugby)
Everyone likes icecream Noone dislikes icecream
"x Likes (x, icecream)  $x Likes(x, icecream)
136
First-Order Predicate Calculus cont…
• "is a conjunction over the universe of objects
• $ Is a disjunction over the universe of objects
"x P
"x P
"x P
"x P




$x P
$x P
$x P
$x P
137
De Morgan’s Laws
PQ
PQ)
PQ
PQ)




(PQ)
PQ
PQ)
PQ
138
Using First-Order Predicate Calculus
1. Marcus was a man
2. Marcus was a Pompeian
3. All Pompeians were Romans
4. Caesar was a ruler
5. All Romans were either loyal to Caesar or hated
him
139
6. Everyone is loyal to someone
7. People only try to assassinate rulers they are
not loyal to
8. Marcus tried to assassinate Caesar
Was Marcus loyal to Caesar?
Prove  loyalto(Marcus, Caesar)
140
• Turn the following sentences into
formulae in first order predicate logic
•
•
•
•
•
•
John likes all kinds of food
Apples are food
Chicken is food
Anything anyone eats and isn’t killed by is food
Bill eats peanuts and is still alive
Sue eats everything Bill eats
• Prove that John likes peanuts using backward
chaining
141
A little bit of Prolog
• Objects and relations between objects
• Facts and rules
parent(pam, bob).
parent(tom, liz).
parent(bob, pat).
parent(tom,bob).
parent(bob, ann).
parent(pat, jim).
? parent(bob, pat).
? parent(bob, liz).
? parent(bob, ben).
? parent(bob, X).
? parent(X, Y).
142
Prolog
grandparent (X,Y) :- parent(X, Z), parent(Z, Y).
For all X and Y
X is the grandparent of Y if
X is a parent of Z and
Z is a parent of Y
sister (X,Y) :- parent(Z, X), parent(Z, Y), female(X)
For all X and Y
X is the sister of Y if
Z is the parent of both X and Y and
X is a female
143