Download Elec Structure of Atom

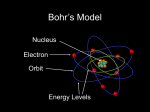
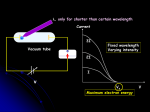
Electronic Structure of Atoms:
Chapter 6, Sections 1-4
6.1 The Wave Nature of Light
Electronic structure – describes energies and
arrangement of electrons around .
 Electromagnetic radiation – radiant energy –
carries energy through space – it moves
through a vacuum at the speed of light (3 x
108 m/s).


It has electric and magnetic components that are
in a wave-like structure.
6.1 The Wave Nature of Light

Waves are described in terms of:
Wavelength λ: distance between peaks
 Frequency ν: periods per unit time
 v λ=c ; c = speed of light

6.2 Quantized Energy and Photons
The minimum amount of radiant energy that
an object can gain or lose is related to the
frequency of the radiation: E=hv.
 Planck’s constant; h=6.63 x 10-34 J-s.
 Energy is quantized, meaning it can only
have certain allowed values.
 Einstein proposed that that light behaves as
if it consisted of quantized energy packets
called photons. Each photon carries energy,
E=hv.

6.3 Bohr’s Model of the Hydrogen
Atom




Spectrum: produced by dispersion of radiation into
its component wavelengths.
Continuous spectrum: contains all wavelengths.
Line spectrum: contains only certain wavelengths.
En represents the energy of the hydrogen atom. (n)
is the principal quantum number and the energy of
the atom increases as n increases.
6.3 Bohr’s Model of the Hydrogen Atom


Use the following equation to relate the frequency
of absorbed or emitted light and the principal
quantum numbers of the two states.
∆E
Rh 1 - 1
v = h = h n 2i
n 2f
Rh is known as Rhydberg’s constant
2.18 x 10-18 J
h is Planck’s constant
6.63 x 10 -34 Js
Wavelength to frequency
_c_
λ= v
Be careful that you convert from nm or
Angstroms to meters so that you units match.
6.3 Bohr’s Model of the Hydrogen
Atom




The lowest energy level is achieved in the ground
state where n=1.
Other n values correspond to excited states.
Light is emitted when the electron drops from a
high energy state to a low energy state; light can be
absorbed to excite the electron from a low energy
state to a high energy state.
The frequency of light emitted or absorbed must be
such that hv=the difference in energy between two
allowed states of the atom.
6.4 The Wave Behavior of Matter





Radiation appears to have either a wavelike or a
particle-like (photon) character
Louis De Broglie (1892-1987) suggested that the
electron in its movement about the nucleus has
associated with it a particular wavelength
De Broglie proposed that wavelength of an electron
depends on its mass and velocity
λ= h/mv; wavelength = Planck’s constant/
momentum (mass x velocity)
De Broglie used the term matter waves to describe
the wave characteristics of material particles
6.4 The Wave Behavior of Matter


German physicist Werner Heisenburg concluded
that the dual nature of matter places a fundamental
limitation on how precisely we can know both the
location and the momentum of any object
Heisenburg’s principle is called the uncertainty
principle which states that it is inherently
impossible for us to know simultaneously both the
exact momentum of an electron and its exact
location in space
Thanks to

Alex Kawa, Kate Harkness, Will Lambert,
Adam Robinson, Tori Waldron, Ankush
Khullar