Download PPT

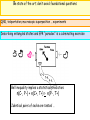
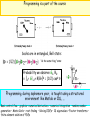
Classes which prepare students
for research, and visa-versa
John Boccio and Amy Bug
Dept. of Physics and Astronomy
Swarthmore College
Undergraduate Student Research is a
good thing
(proof forthcoming …)
Excitement of being engaged in pushing the limits
of our current knowledge S. Brubaker-Cole, Stanford Univ.
Newsletter, Spring 2002
A good way to connect … faculty and students
J. Mervis, Science Aug. 31, 2001
The goal of integrating research and education is to
teach students to understand and apply the
scientific method Reed College NSF-AIRE website, download June, 2002
Undergraduate student research in physics …
(specifically theoretical/computational quantum physics)
Special benefits? Special difficulties?
Benefits
Recruitment and Retention of physics majors
R. and R. of nontraditional students
Intellectual ones … lab and classroom are complimentary settings in which to learn the same physics
“(We) teach students how to learn from a variety of sources, including books,
journals, experiments, colleagues, modeling, and simulations. Encourage
independent investigation.” - Harvey Mudd College Physics website, June 2002
Proposal: The earlier research is integrated into a
student’s career, the better.
Difficulties
A relatively slow maturation rate under the standard physics curriculum.
When should we teach quantum mechanics and at what level?
There is no typical first-two-years-curriculum.
Here is one:
Classical physics I, II and III (Serway and Beichner, Wolfson and Pasachoff, etc.) followed by ...
2XX. MODERN PHYSICS (1 credit )
An introduction to the elementary theoretical aspects of special relativity, quantum mechanics, atomic and nuclear structure,
and a few selected topics from solid state physics and particle physics. The course presents the structure of these theories
and how they differ from corresponding classical theories, and some historical and philosophical aspects of the theories.
Class discussion and demonstrations. Prerequisites: PHY-2XX, concurrent enrollment in PHY-2XX, or permission of instructor.
Spring semester.
2XX. APPLIED MATHEMATICS FOR PHYSICS AND ENGINEERING (.5 credit)
An introduction to Fourier series, series solutions to differential equations, special functions, partial differential equations,
linear equations, vectors, matrices and determinants, and coordinate transformations. Emphasis will be placed on the
mathematics needed to describe physical systems. Three lectures weekly. Prerequisites: XXX. Spring semester.
Research-friendly teaching Ideas :
Permute the order; teach quantum physics to freshmen
Formal techniques come first; not history, or even phenomenology
Be state-of-the-art; don’t avoid foundational questions
Programming is a part of every course
(Computational lab within a sophomore math methods course)
Require nontraditional activities: programs, lab projects, essays
Permute the order; teach quantum physics to freshmen
“The Character of Physical Law” teaches freshman-level
relativity and quantum mechanics
texts: Mermin, Moore, ...
texts: various, none optimal … lecture notes!
Formal techniques come first
Excerpts from The Stanford Encyclopedia of Philosophy:
The heart and soul of quantum mechanics is contained in the Hilbert spaces that represent the state-spaces of quantum mechanical systems.
The internal relations among states and quantities, and everything this entails about the ways quantum mechanical systems behave, are all
woven into the structure of these spaces, embodied in the relations among the mathematical objects which represent them.[4] This means that
understanding what a system is like according to quantum mechanics is inseparable from familiarity with the internal structure of those
spaces.. … Graduate students in physics spend long years gaining familiarity with the nooks and crannies of Hilbert space, locating familiar
landmarks, treading its beaten paths, learning where secret passages and dead ends lie, and developing a sense of the overall lay of the land.
They learn how to navigate Hilbert space in the way a cab driver learns to navigate his city ...
Vectors and vector spaces
A vector A, written ‘|A>’, is a mathematical object characterized by a length, |A|, and a direction. A normalized vector is a vector of
length 1; i.e., |A| = 1. Vectors can be added together, multiplied by constants (including complex numbers), and multiplied together.
Vector addition maps any pair of vectors onto another vector, specifically, the one you get by moving the second vector so that it’s
tail coincides with the tip of the first, without altering the length or direction of either ... So, for example, adding vectors |A> and |B>
yields vector |C> (= |A> + |B>) as in Figure 1:
Teach algebra of states and operators using Dirac notation
“Quon” states are labeled by quantum
numbers like color
<G|G> = 1
<M|M> = 1
<G|M> = <M|G> = 0
(by definition)
(ditto)
(ditto)
Operators act on states to
produce new states (sometimes
just an eigenvalue times the old
state …) O |A> = |B>
E.g. PG |A> = PG ( aG |G> + aM |M> ) = aG |G> = |f>
|A> = aM |M> + aG |G>
C|G> = +1 |G> ; C|M> = -1 |M>
aM*aM + aG*aG = 1
One can show that non-commuting
operators exist
One can use the probability
postulate to find the results
of measurements (expectation values)
|R>
|<G|R >|2
|<M|R >|2
CT|R> = C (+1)|R> = C|R> = (|G >/√2 - |M >/√2) = |S >
and
TC|R> = T(|G >/√2 - |M >/√2) = T|S> = (-1) |S > = -|S >
Various important ideas emerge: quantization, coherent
superposition, Heisenberg uncertainty principle,
measurements give one member of an eigenspectrum, ...
Students
•can do novel calculations
•learn of, but are not dependant on
particular instantiations: krazy kaons,
electrons, double slits, polarized photons...
•are not asked to unlearn classical physics
Be state of the art; don’t avoid foundational questions
QND, teleportation, macroscopic superposition ... experiments
Describing entangled states and EPR “paradox” is a culminating exercise
Bell inequality implies a statistical prediction:
n(C-, P-) + n(C+, T+) > n(P-, T+)
Identical pairs of socks are tested …
Programming is a part of the course
Socks are in entangled, Bell state:
“do the same thing” state
Probability we observe G1, R2
= |1< G| 2< R|B>|2 = (1/2) cos2 q
Programming, during sophomore year, is taught using a structured
environment like Matlab or IDL, ...
Basic control flow • graphics• numerical derivatives • numerical integration • random number
generation • Monte Carlo • root-finding • Solving ODE’s • 1D eigenvalues • Fourier transforms •
finite-element solution of PDEs
Require nontraditional activities: journal
Case study involving computational physics research
Goal: Simulation of
Positron Annihilation in Materials
An undergraduate student, with the aforementioned experience in
quantum mechanics and some programming ability (or willingness to learn) is
able to participate very fully in this research.
Motivation: Positron Annihilation Spectroscopy (PAS)
provides information on size and chemical
content of pores and defects in solids
e+ enters solid
and thermalizes
within tens of ps;
e+ preferentially
locates in
channels and cavities
e+ selects electron
of solid and forms
positronium (Ps) with
natural lifetime of
125 ps (para) or
140 ns (ortho)
e+ in Ps is “picked
off” prematurely by
another electron
of solid
two gamma rays
with characteristic
energy of 511 keV
are emitted
Lifetime, t , of Ps is properly determined by electronic
density r-:
t-1 = p r 2 c ∫ dr dr r (r ) r (r ) g[r ( r )] d3(r - r )
e
-
+
+
+
-
-
-
-
-
+
Method: We simulate Ps in solids via
Path Integral Monte Carlo (PIMC)
and Density Functional Theory (DFT)
e+
e-
Ps “chains”
simulated Ps probability
density within solid
Codes are written by students in Fortran 9X and run both on Linux
workstation and Appleseed Macintosh cluster using Mac MPI libraries.
Ideas and ingredients of PIMC method (1):
Positron has state |Y>
research
The overlap of the state with another
one, say |ri >, is <ri| Y >, the amplitude
for measuring positron located at ri .
|amplitude|2 is observable: the probability
You can always insert a complete set of
states into any calculated quantity:
∑i | ri> <ri | = 1
(Actually, ∫ | r> <r| dr = 1)
but ...
Quon has state |A >
course
The overlap of the state with
another one, say |G>, is <G|A>, the amplitude
for measuring a green positron.
|amplitude|2 is observable: the probability
|G> <G | + |M> <M| = 1
Ideas and ingredients of PIMC method (2):
research
Might want the expectation value of
the density matrix operator. An
average over all quantum states in a
complete basis
ˆ 
Z   r
 ri | rˆ | ri 
i
Student needs to further know/believe
• you can exponentiate an operator
• an operator commutes with itself
• <x|p> = e i px
•
ˆ
ˆ
H
Vˆ
• how
doa Gaussian
to
e-to
e-T e-integral
arrive at
course
Might want the expectation value of
an operator as an average
over all quantum states in a
complete basis:
Z = < I > = <R| I|R> + <S| I|S>
Ideas and ingredients of PIMC method (2):
research
Might want the expectation value of
the density matrix operator. An
average over all quantum states in a
complete basis
ˆ 
Z   r
 ri | rˆ | ri 
i
Student needs to further know/believe
• you can exponentiate an operator
• an operator commutes with itself
• <x|p> = e i px
•
ˆ
ˆ
H
Vˆ
• how
doa Gaussian
to
e-to
e-T e-integral
arrive at
course
Might want the expectation value of
an operator as an average
over all quantum states in a
complete basis:
Z = < I > = <R| I|R> + <S| I|S>
Ideas and ingredients of PIMC method (2):
research
Might want the expectation value of
the density matrix operator. An
average over all quantum states in a
complete basis
ˆ 
Z   r
 ri | rˆ | ri 
i
Student needs to further know/believe
• you can exponentiate an operator
• an operator commutes with itself
• <x|p> = e i px
•
ˆ
ˆ
H
Vˆ
• how
doa Gaussian
to
e-to
e-T e-integral
arrive at
course
Might want the expectation value of
an operator as an average
over all quantum states in a
complete basis:
Z = < I > = <R| I|R> + <S| I|S>
Ideas and ingredients of PIMC method (2):
research
Might want the expectation value of
the density matrix operator. An
average over all quantum states in a
complete basis
ˆ 
Z   r
 ri | rˆ | ri 
i
Student needs to further know/believe
• you can exponentiate an operator
• an operator commutes with itself
• <x|p> = e i px
•
ˆ
ˆ
H
Vˆ
• how
doa Gaussian
to
e-to
e-T e-integral
arrive at
course
Might want the expectation value of
an operator as an average
over all quantum states in a
complete basis:
Z = < I > = <R| I|R> + <S| I|S>
Ideas and ingredients of PIMC method (2):
research
Might want the expectation value of
the density matrix operator. An
average over all quantum states in a
complete basis
ˆ 
Z   r
 ri | rˆ | ri 
i
Student needs to further know/believe
• you can exponentiate an operator
• an operator commutes with itself
• <x|p> = e i px
•
ˆ
ˆ
H
Vˆ
• how
doa Gaussian
to
e-to
e-T e-integral
arrive at
course
Might want the expectation value of
an operator as an average
over all quantum states in a
complete basis:
Z = < I > = <R| I|R> + <S| I|S>
Ideas and ingredients of PIMC method (2):
research
Might want the expectation value of
the density matrix operator. An
average over all quantum states in a
complete basis
ˆ 
Z   r
 ri | rˆ | ri 
i
Student needs to further know/believe
• you can exponentiate an operator
• an operator commutes with itself
• <x|p> = e i px
•
ˆ
ˆ
H
Vˆ
• how
doa Gaussian
to
e-to
e-T e-integral
arrive at
course
Might want the expectation value of
an operator as an average
over all quantum states in a
complete basis:
Z = < I > = <R| I|R> + <S| I|S>
Ideas and ingredients of PIMC method (2):
research
Might want the expectation value of
the density matrix operator. An
average over all quantum states in a
complete basis
ˆ 
Z   r
 ri | rˆ | ri 
i
Student needs to further know/believe
• you can exponentiate an operator
• an operator commutes with itself
• <x|p> = e i px
•
ˆ
ˆ
H
Vˆ
• how
doa Gaussian
to
e-to
e-T e-integral
arrive at
course
Might want the expectation value of
an operator as an average
over all quantum states in a
complete basis:
Z = < I > = <R| I|R> + <S| I|S>
Ideas and ingredients of PIMC method (2):
research
Might want the expectation value of
the density matrix operator. An
average over all quantum states in a
complete basis
ˆ 
Z   r
 ri | rˆ | ri 
i
Student needs to further know/believe
• you can exponentiate an operator
• an operator commutes with itself
• <x|p> = e i px
•
ˆ
ˆ
H
Vˆ
• how
doa Gaussian
to
e-to
e-T e-integral
arrive at
course
Might want the expectation value of
an operator as an average
over all quantum states in a
complete basis:
Z = < I > = <R| I|R> + <S| I|S>
Ideas and ingredients of PIMC method (2):
research
Might want the expectation value of
the density matrix operator. An
average over all quantum states in a
complete basis
ˆ 
Z   r
 ri | rˆ | ri 
i
Student needs to further know/believe
• you can exponentiate an operator
• an operator commutes with itself
• <x|p> = e i px
•
ˆ
ˆ
H
Vˆ
• how
doa Gaussian
to
e-to
e-T e-integral
arrive at
course
Might want the expectation value of
an operator as an average
over all quantum states in a
complete basis:
Z = < I > = <R| I|R> + <S| I|S>
Ideas and ingredients of PIMC method (2):
research
Might want the expectation value of
the density matrix operator. An
average over all quantum states in a
complete basis
ˆ 
Z   r
 ri | rˆ | ri 
course
Might want the expectation value of
an operator as an average
over all quantum states in a
complete basis:
Z = < I > = <R| I|R> + <S| I|S>
i
ˆ | ri 
 ri | r
is the probability (density)
to be found at location ri
ri
PIMC method yields the thermal probability density
ˆ | ri 
 ri | r
ri
is the probability (density)
to be found at location ri
e+ and e- 1000-bead chains
frequency
frequency
Two free, 1000-bead chains
xi, yi, zi (a.u)
xi, yi, zi (a.u)
Binning the relative coordinate gives you
density corresponding to the orbital (here, ground state)
Number, ni, of beads
in bin from r to r + dr
Normalized so that
Si ni dr = 1
P (r) /r2 a.k.a. |R(r)|2
P (r)
From a student’s writeup:
The harmonic oscillator
Can calculate other observables:
 Hˆ 
(there is some numerical art to this … )
 rˆ 
V(r) = e E z
a ≈ 36 a.u.
Research gets done, students get trained:
•Student Posters
•Conference talks
•Theses
•Papers
•Grants
•Classroom-type understanding?
Ps electron in FCC Argon
Unsolved problems:
•Reading the literature (Help us, AJP!)
•Research that relies on Relativistic QM (or foundations of
QM, quantum gravity; which are not problems for the
best students, but … )
•Early preparation in statistical mechanics
(MIT model: Do it
soph year. Radical idea: Make room in first-year classical
mechanics. E.g. Leave massive pulleys and rolling stuff for
later. Why do stuff twice? Why not do Lagrangians instead?)