Download P202 Lecture 2

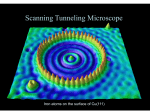
Schrodinger’s Equation Solutions
Finite Square Well
For this case, you must solve a transcendental equation to find the solutions that
obey the boundary conditions (in particular, continuity of the function and its
derivative at the well boundary). For the geometry we considered in class, this
takes on one of two forms: Even solutions k=k tan(ka/2) ;
Odd solutions k= -k cot(ka/2)
Recall from class that we can recast
the transcendental equation into a
dimensionless form, where the
controlling parameter is the ratio of
the potential well depth to the
“confinement energy”. You can get
the spreadsheet for the even
solutions from the website:
http://physics.indiana.edu/~courses/p
301/F09/Homework/
The fig. shows the marginal case for
two even solutions (3 overall) a=p2
9
7
5
LHS
3
RHS
1
-1 0
-3
-5
0.2
0.4
0.6
0.8
1
1.2
Schrodinger’s Equation Solutions
Harmonic Oscillator
There are an infinite number of
possible states, since the potential
is defined to keep going up (of
course this is an idealization).
Interestingly, the energy levels are
evenly spaced in this case:
E = hw(n + ½)
n = 0, 1, 2, …
Schrodinger’s Equation Solutions
Harmonic Oscillator
n=10
Notice how the quantum
probability distribution (blue
curve) gets closer to the
classical one (dashed line
above) as n gets bigger.
n=0
Quantum Tunneling in Chemistry
McMohan
Science 299,
833 (2003)
Lecture 22
Potential Barrier: Classical
Transmitted
Reflected
E >Vo
<Vo
Lecture 22
Potential Barrier: Quantum
E <Vo
Reflected and
Transmitted !!
You can watch a demonstration of the optical analog of this on YouTube at:
http://www.youtube.com/watch?v=aC-4iSD2aRA
Lecture 22
JITT question
Identify two examples of phenomena discussed in the
text where quantum mechanical tunneling is involved,
and cast a vote for which one you would like to see
discussed in greater detail in class.
•Alpha-decay (18 identified this; 13.5 voted for it)
•Tunnel diodes (16 identified this; 4 voted for it)
•STM (2 identified this, ½ voted for it)
•Internal reflection of light (2 identified it; one voted for it)
•Potential wells and barriers (3 identified these; 1 voted for it)
Lecture 23
Intro to Radioactivity
This chart shows the decay
modes of the known nuclides,
see the link for an interactive
version with lots more
information
http://www.nndc.bnl.gov/chart/reColor.jsp?newColor=dm
Lecture 23
Potential Barrier: Alpha Decay
Alpha decay in
radioactivity
The narrow “squarish” well is
provided by the STRONG force,
but once the a particle gets far
enough away from the other
nucleons, it feels the Coulomb
repulsion. The a particle ‘leaks’
through the triangle-like barrier.
The energy level (above 0) Ea,
determines the half-life of the
nucleus (i.e. how rapidly the
particle tunnels out of the
nuclear barrier).
Nuclear potential
Lecture 23
Potential Barrier: Alpha decay
The deeper the “bound” state is below the top of the barrier, the lower will be
the kinetic energy of the alpha particle once it gets out, and the slower will be
the rate of tunneling (and hence the longer the half-life). Figures from Rohlf
“Modern Physics from a to Zo”.
Lecture 23
JITT question
The STM was the first of what is now a wide assortment
of scanning probe microscopies for studying surfaces
(Atomic Force, Magnetic Force, Scanning capacitance,
Near-field Scanning Optical …). How would you expect
the current in an STM to depend on the separation
between the tip and the surface?
•“decrease as the distance increases” (13 responses)
•Inversely as the square of the distance (Coulomb) (2 responses
•Exponential decay with distance (4 response)
• Other (9 responses)
•No response (12)
What defines “the surface” in this technique?
•“the Surface” (4 responses)
•The surface atoms (6 responses)
•The “upper electrons” (10 responses)
•The boundary of the well (3 response)
Lecture 23
Scanning Tunneling Microscope
Basic operation of the STM. Piezo-electric actuators move the tip in three
directions, typically keeping the current constant and the “surface” is mapped
out by monitoring the “z” feedback voltage as the x-y directions are scanned.
(the exponential dependence of current on separation is crucial to this).
http://www.ieap.uni-kiel.de/surface/ag-kipp/stm/images/stm.jpg
Lecture 23
Scanning Tunneling Microscope
“High-Resolution” STM measurement of the a surface of Si (7x7 reconstruction
of the 111 surface, if you wan to be technical), along with a computer
calculation of the electron density predicted for that surface, and a “stick”
model of the atomic positions. Taken from the Omictron site:
http://www.omicron.de/index2.html?/results/highest_resolution_stm_image_of_si_111_7x7/index.html~Omicron
Lecture 23
Scanning Tunneling Microscope
Fe atoms arranged by “hand” into a circle on a Cu surface (111 surface to be
precise) The ripples inside the “corral” represent the states available to the
electrons in the copper in the presence of these extra surface atoms.
http://www.almaden.ibm.com/vis/stm/stm.html
See also: http://www.youtube.com/watch?v=0wF4f2YadoA
Lecture 24
Spherical Polar Coordinates
http://en.wikipedia.org/wiki/Spherical_coordinate_system
http://en.citizendium.org/wiki/Spherical_polar_coordinates
•r defines the sphere
•q defines the cone
•f defines the plane and
• the intersection of the
three is the point of
interest
Lecture 24
Spherical Harmonics
http://www.physics.umd.edu/courses/Phys402/AnlageSpring09/spherical_harmonics.gif
Lecture 24
Spherical Harmonics
http://en.wikipedia.org/wiki/Atomic_orbital
Lecture 24
The Hydrogen Atom revisited
Major differences between the “QM” hydrogen
atom and Bohr’s model (my list):
•The electrons do not travel in orbits, but in well defined states
(orbitals) that have particular shapes (probability distributions
for the electrons, or linear combinations thereof) [9 responses]
•The Energy levels are NOT tied directly to the angular
momentum. [2 responses]
•There are several different states with the same energy in the
QM atom [4 answers addressed this but in different words]
•Angular momentum is more involved, and more subtle than in
the Bohr atom [3 responses]
NOTE: the energy levels are (nominally) the same,
until we account for subtle effects that lift degeneracy.