* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download 4. Statistics Review 1 - essie-uf
Inductive probability wikipedia , lookup
Degrees of freedom (statistics) wikipedia , lookup
Foundations of statistics wikipedia , lookup
History of statistics wikipedia , lookup
Bootstrapping (statistics) wikipedia , lookup
Confidence interval wikipedia , lookup
Law of large numbers wikipedia , lookup
German tank problem wikipedia , lookup
Misuse of statistics wikipedia , lookup
Resampling (statistics) wikipedia , lookup
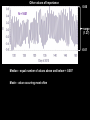
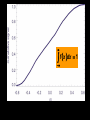
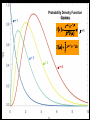
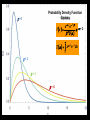
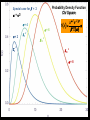
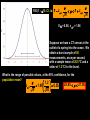
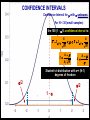
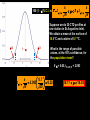
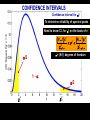
BASIC STATISTICAL CONCEPTS Statistical Moments & Probability Density Functions Ocean is not “stationary” Population Sample “Stationary” - statistical properties remain constant in time Data collected have signal and noise Both signal and noise are assumed to have random behavior Most basic descriptive parameter for any set of measurements: 1 N x xi N i 1 Sample Mean over the duration of a time series – “time average” or over an ensemble of measurements – “ensemble mean” Sample mean is an unbiased estimate of the population mean ‘’ The population mean, μ, can be regarded as the expected outcome E(y) of an event y. If the measurement is executed many times, μ would be the most common outcome, i.e., it’d be E(y) (e.g. the weight printed on a bag of chips) Sample Mean - locates center of mass of data distribution such that: N 1 N xi x 0 x ' N i 1 i 1 Weighted Sample Mean 1 N x fi x i N i 1 fi N relative frequency of occurrence of i th value Variance - describes spread about the mean or sample variability Sample variance 1 N s' x i x N i 1 2 Sample standard deviation 2 s' s'2 typical difference from the mean 1 N xi x Population variance (unbiased) N 1 i 1 2 2 N needs to be > 1 to define variance and std dev Only for N < 30 s’ and are significantly different 2 N N 1 1 2 2 Computationally more efficient x i x i N 1 i 1 N i 1 (only one pass through the data) Population variance 1 N xi x N 1 i 1 2 Sample variance 2 x N has one degree of freedom (dof) < s '2 1 N i 1 i x 2 because we estimate population variance with sample variance (one less dependent measure) d.o.f. : = # of independent pieces of data being used to make a calculation. = measure of how certain we are that our sample is representative of the entire population The larger the more certain we are that we have sampled the entire population Example: we have 2 observations, when estimating the mean we have 2 independent observations: = 2 But when estimating the variance, we have one independent observation because the two observations are at the same distance from the mean: =1 Other values of Importance 0.66 N = 1601 range (1.27) -0.61 Median – equal number of values above and below = -0.007 Mode – value occurring most often Mode = -0.3 Two Modes Bimodal Probability Provides procedures to infer population distribution from sample distribution and to determine how good the inference is The probability of a particular event to occur is the ratio of the number of occurrences of that event and the total number of occurrences for all possible events P (a dice showing ‘6’) = 1/6 0 P (x) 1 The probability of a continuous variable is defined by a PROBABILITY DENSITY FUNCTION -- PDF Probability is measured by the area underneath PDF f x dx 1 f x dx 1 Probability Density Function Gauss or Normal or Bell f x x 2 2 2 e 2 erf(2/(2)½) = 95.4% 3 2 erf(1/(2)½) = 68.3% 1 erf(3/(2)½) = 99.7% Probability Density Function Gauss or Normal or Bell F z z e z2 2 2 x standardized normal variable 68.3% 3 1 2 95.4% 99.7% Probability Density Function Gamma =1 x 1e x f x =1 x 1e x dx 0 =2 =3 =4 Probability Density Function Gamma =1 x 1e x = 2 f x x 1e x dx 0 =2 =3 =4 Special case for = 2 Probability Density Function Chi Square = /2 =4 =2 4 2 8 =6 2 x 1e x f x 12 2 16 2 =8 CONFIDENCE INTERVALS Confidence Interval for with known For N > 30 (large enough sample) the 100 (1 - )% confidence interval is: x z 2 N x z 2 z N x standardized normal variable /2 /2 1- (1 - /2) = 0.975 z /2 = 1.96 http://statistics.laerd.com/statistical-guides/normal-distribution-calculations.php 100 (1 - )% C.I. is: x z 2 N x z 2 N If = 0.05, z /2 = 1.96 Suppose we have a CT sensor at the outlet of a spring into the ocean. We obtain a burst sample of 50 measurements, once per second, with a sample mean of 26.5 ºC and a stdev of 1.2 ºC for the burst. What is the range of possible values, at the 95% confidence, for the population mean? z 2 1.2 1.96 0.55 N 50 25.95 27.05 CONFIDENCE INTERVALS Confidence Interval for with unknown For N < 30 (small samples) the 100 (1 - )% confidence interval is: x t 2, t s s x t 2, N N x s N z x Student’s t-distribution with = (N-1) degrees of freedom /2 /2 1- /2 = 0.025 d.o.f.= 19 100 (1 - )% C.I. is: x t 2, s s x t 2, N N Suppose we do 20 CTD profiles at one station in St Augustine Inlet. We obtain a mean at the surface of 16.5 ºC and a stdev of 0.7 ºC . /2 1- /2 What is the range of possible values, at the 95% confidence, for the population mean? If = 0.05, t0.025,19 = 2.093 t 2, s 0.7 2.093 0.33 N 20 16.17 16.83 CONFIDENCE INTERVALS Confidence Interval for 2 To determine reliability of spectral peaks Need to know C.I. for 2 on the basis of s2 N 1s 2 2, 2 2 12 2, = (N-1) degrees of freedom /2 1- /2 L2 N 1s 2 U2 100 (1 - )% C.I. is: N 1s 2 2, 2 2 N 1s 2 12 2, Suppose that we have = 10 spectral estimates of a tidal record. /2 1- L2 /2 The background variance near a distinct spectral peak is 0.3 m2 95% C.I. for variance? U2 How large would the peak have to be to stand out, statistically, from background level? /2 = 0.025; 1 - /2 = 0.975 Look at Chi square table: P 3.25 210 20.48 1 N 1s 2 2, 2 2 N 1s 2 2 1 2 , 100.3 20.48 2 100.3 3.25 0.15 2 0.92 The background variance lies in this range The spectral peak has to be greater than 0.92 m2 to distinguish it from background levels Chi Square Table