Download 4. Statistics Review 1 - essie-uf

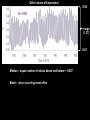
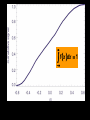
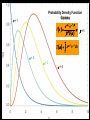
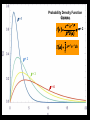
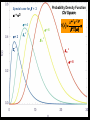
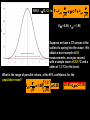
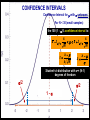
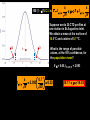
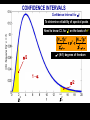
BASIC STATISTICAL CONCEPTS
Statistical Moments & Probability Density Functions
Ocean is not “stationary”
Population
Sample
“Stationary” - statistical properties remain constant in time
Data collected have signal and noise
Both signal and noise are assumed to have random behavior
Most basic descriptive parameter for any set of measurements:
1 N
x   xi
N i 1
Sample Mean
over the duration of a time series – “time average”
or over an ensemble of measurements – “ensemble mean”
Sample mean is an unbiased estimate of the population mean ‘’
The population mean, μ, can be regarded as the expected outcome E(y) of an
event y.
If the measurement is executed many times, μ would be the most common
outcome, i.e., it’d be E(y) (e.g. the weight printed on a bag of chips)
Sample Mean - locates center of mass of data distribution such that:


N
1 N
xi  x  0   x '

N i 1
i 1
Weighted Sample Mean
1 N
x   fi x i
N i 1
fi
N
relative frequency of occurrence of i th value
Variance - describes spread about the mean or sample variability
Sample variance

1 N
s'   x i  x
N i 1
2
Sample standard deviation

2
s'  s'2 typical difference from the mean

1 N
xi  x
Population variance (unbiased)  

N  1 i 1
2

2
N needs to be > 1 to define variance and std dev
Only for N < 30 s’ and  are significantly different
2
N
N

 
1
1
2
2
Computationally more efficient
 
  x i     x i  
N  1  i 1
N  i 1  
(only one pass through the data)
Population variance

1 N
 
xi  x

N  1 i 1
2

Sample variance
2

x

N
has one degree of freedom (dof) < s '2  1
N
i 1
i
x

2
because we estimate population variance with sample variance
(one less dependent measure)
d.o.f. :  = # of independent pieces of data being used to make a calculation.
 = measure of how certain we are that our sample is representative of
the entire population
The larger  the more certain we are that we have sampled the entire population
Example: we have 2 observations, when estimating the mean we have 2
independent observations:  = 2
But when estimating the variance, we have one independent observation
because the two observations are at the same distance from the mean:  =1
Other values of Importance
0.66
N = 1601
range
(1.27)
-0.61
Median – equal number of values above and below = -0.007
Mode – value occurring most often
Mode = -0.3
Two Modes
Bimodal
Probability
Provides procedures to infer population distribution from sample distribution
and to determine how good the inference is
The probability of a particular event to occur is the ratio of the number of
occurrences of that event and the total number of occurrences for all
possible events
P (a dice showing ‘6’) = 1/6
0
P (x)
1
The probability of a continuous variable is defined by a PROBABILITY
DENSITY FUNCTION -- PDF
Probability is measured by the area underneath PDF

 f  x dx  1


 f  x dx  1

Probability Density Function
Gauss or Normal or Bell
f x  

  x   2 2 2 
e
 2

erf(2/(2)½)
= 95.4%
3
2
erf(1/(2)½)
= 68.3%
1
erf(3/(2)½)
= 99.7%
Probability Density Function
Gauss or Normal or Bell
F z  
z
e
 z2 2
2
x

standardized normal variable

68.3%
3
1
2
95.4%
99.7%
Probability Density Function
Gamma
=1
x  1e  x 
f x   
 =1
  

     x  1e  x dx
0
=2
=3
=4
Probability Density Function
Gamma
=1
x  1e  x   = 2
f x   

  

     x  1e  x dx
0
=2
=3
=4
Special case for  = 2
Probability Density Function
Chi Square
 = /2
=4
=2
4 2
8
=6
2
x  1e  x 
f x   

  
12 2
16 2
=8
CONFIDENCE INTERVALS
Confidence Interval for  with  known
For N > 30 (large enough sample)
the 100 (1 - )% confidence interval is:
x  z 2

N
   x  z 2
z

N
x

standardized normal variable
/2
/2
1-
(1 - /2) = 0.975
 z /2 = 1.96
http://statistics.laerd.com/statistical-guides/normal-distribution-calculations.php
100 (1 - )% C.I. is: x  z 2

N
   x  z 2

N
If  = 0.05, z /2 = 1.96
Suppose we have a CT sensor at the
outlet of a spring into the ocean. We
obtain a burst sample of 50
measurements, once per second,
with a sample mean of 26.5 ºC and a
stdev of 1.2 ºC for the burst.
What is the range of possible values, at the 95% confidence, for the
population mean?
z 2

 1.2 
 1.96
  0.55
N
 50 
25.95    27.05
CONFIDENCE INTERVALS
Confidence Interval for  with  unknown
For N < 30 (small samples)
the 100 (1 - )% confidence interval is:
x  t 2,
t
s
s
   x  t 2,
N
N
x
s N
z
x

Student’s t-distribution with  = (N-1)
degrees of freedom
/2
/2
1-
/2 = 0.025
d.o.f.= 19
100 (1 - )% C.I. is: x  t
2,
s
s
   x  t 2,
N
N
Suppose we do 20 CTD profiles at
one station in St Augustine Inlet.
We obtain a mean at the surface of
16.5 ºC and a stdev of 0.7 ºC .
/2
1-
/2
What is the range of possible
values, at the 95% confidence, for
the population mean?
If  = 0.05, t0.025,19 = 2.093
t 2,
s
 0.7 
 2.093
  0.33
N
 20 
16.17    16.83
CONFIDENCE INTERVALS
Confidence Interval for 2
To determine reliability of spectral peaks
Need to know C.I. for 2 on the basis of s2
N  1s 2
 2,
2
 
2
 12 2,
 = (N-1) degrees of freedom
/2
1-
/2
 L2
N  1s 2
 U2
100 (1 - )% C.I. is:
N  1s 2
 2,
2
 
2
N  1s 2
 12 2,
Suppose that we have  = 10
spectral estimates of a tidal record.
/2
1-
 L2
/2
The background variance near a
distinct spectral peak is 0.3 m2
95% C.I. for variance?
 U2
How large would the peak have to be
to stand out, statistically, from
background level?
/2 = 0.025; 1 - /2 = 0.975
Look at Chi square table:
P 3.25  210  20.48   1  
N  1s 2
  2,
2
 
2
N  1s 2

2
1 2 ,

100.3
20.48
 
2
100.3
3.25
0.15   2  0.92
The background variance lies in this range
The spectral peak has to be greater than 0.92 m2 to distinguish it from
background levels
Chi Square Table