* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Calculus 1.5
Survey
Document related concepts
Transcript
1.5 Logarithms
QuickTime™ and a
decompressor
are needed to see this picture.
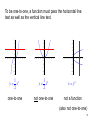
A relation is a function if:
for each x there is one and only one y.
A relation is a one-to-one if also:
for each y there is one and only one x.
In other words, a function is one-to-one
on domain D if:
f a f b whenever a b
To be one-to-one, a function must pass the horizontal line
test as well as the vertical line test.
5
5
5
4
4
4
3
3
3
2
2
2
1
1
1
-5 -4 -3 -2 -1 0
-1
1
2
3
4
5
-5 -4 -3 -2 -1 0
-1
1
2
3
4
5
-5 -4 -3 -2 -1 0
-1
1
2
3
4
-2
-2
-2
-3
-3
-3
-4
-4
-4
-5
-5
-5
1 3
y x
2
1 2
y x
2
x y2
one-to-one
not one-to-one
not a function
5
(also not one-to-one)
Inverse functions:
f x
1
x 1
2
Given an x value, we can find a y value.
5
1
y x 1
2
4
3
2
1
Solve for x:
-5 -4 -3 -2 -1 0
-1
1
y 1 x
2
-2
-3
-4
2y 2 x
-5
1
2
3
4
5
Inverse functions
are reflections
about y = x.
x 2y 2
Switch x and y:
y 2x 2
f 1 x 2 x 2
(eff inverse of x)
example 3:
Graph:
f x
f x x2
f 1 x
x0
yx
for
x0
a parametrically:
Y=
f : x1 t
y1 t 2
f 1 : x2 t 2
y2 t
y x : x3 t
y3 t
t0
WINDOW
GRAPH
f x x2
example 3:
Graph:
f x
f 1 x
x0
yx
for
x0
b Find the inverse function:
yx
2
WINDOW
x0
Switch x & y:
y x
yx
x y
f 1 x x
Change the graphing mode to function.
Y=
y1 x 2 x 0
y2 x
y3 x
>
GRAPH
Consider
f x ax
This is a one-to-one function, therefore it has an inverse.
The inverse is called a logarithm function.
Example:
16 24
4 log 2 16
Two raised to what power
is 16?
The most commonly used bases for logs are 10: log10 x log x
and e: log e x ln x
y ln x
is called the natural log function.
y log x is called the common log function.
In calculus we will use natural logs exclusively.
We have to use natural logs:
Common logs will not work.
y ln x
is called the natural log function.
y log x is called the common log function.
Even though we will be using natural logs in calculus, you
may still need to find logs with other bases occasionally.
Here is a useful keyboard shortcut for the newer
TI-89 Titanium calculators. (Unfortunately the
shortcut does not work on the older TI-89s.)
7
returns:
log(
If you enter:
log(1000)
you get:
3
(base 10)
If you enter:
log(32, 2)
you get:
5
(base 2)
And while we are on the topic of TI-89
Titanium keyboard shortcuts:
9
returns:
root(
If you enter:
root(16)
you get:
4
(square root)
If you enter:
root(32,5)
you get:
2
(fifth root)
Properties of Logarithms
a
log a x
x
log a a x x
a 0 , a 1 ,
x 0
Since logs and exponentiation are inverse functions, they
“un-do” each other.
Product rule:
log a xy log a x log a y
Quotient rule:
x
log a log a x log a y
y
Power rule:
log a x y log a x
Change of base formula:
y
ln x
log a x
ln a
Example 6:
$1000 is invested at 5.25 % interest compounded annually.
How long will it take to reach $2500?
1000 1.0525 2500
t
1.0525
t
2.5
ln 1.0525 ln 2.5
We use logs when we have an
unknown exponent.
t
t ln 1.0525 ln 2.5
ln 2.5
t
17.9
ln 1.0525
17.9 years
In real life you would have to
wait 18 years.
p*
Example 7:
Indonesian Oil Production (million barrels per year):
1960 20.56
1970 42.10
1990 70.10
Use the natural logarithm
regression equation to estimate
oil production in 1982 and 2000.
How do we know that a logarithmic equation is appropriate?
In real life, we would need more points or past experience.
Indonesian Oil
Production:
60,70,90 L1
2nd
60
70
90
ENTER
{ 60,70,90
2nd
}
STO
2nd
20.56 million
42.10
70.10
L 1
ENTER
20.56, 42.10,70.10 L2
(on a Ti-89)
LnReg L1, L2 ENTER
2nd
MATH
6
Statistics
3
5
2nd
LnReg
Regressions
L1
,
2nd
The calculator
should return:
L2
Done
ENTER
(on a Ti-84)…
LnReg L1, L2, Y1 ENTER
STAT
CALC
9
2nd
L1
,
2nd
L2
,
VARS
LnReg
Y-VARS FUNCTION…
Y1
ENTER
The calculator gives you an
equation and constants:
y a b ln x
a 474.3
b 121.1
We can use the calculator to plot the new curve along with
the original points:
2nd
Y=
Plot1…On
Xlist: L1
Type: Scatter
Ylist: L2
ENTER
WINDOW
GRAPH
WINDOW
GRAPH
What does this
equation predict
for oil production
in 1982 and 2000?
TRACE
This lets us see values for the distinct points.
2ND
Moves to the line.
2ND
CALC
CALC
82
ENTER
Enters an x-value of 82.
In 1982, production was 59 million barrels.
100
ENTER
Enters an x-value of 100.
In 2000, production was 84 million barrels.
p
QuickTime™ and a
decompressor
are needed to see this picture.
1.6 Trig Functions
Trigonometric functions are used extensively in calculus.
When you use trig functions in calculus, you must use radian
measure for the angles. The best plan is to set the calculator
mode to radians and use 2nd
o when you need to use
degrees.
Even and Odd Trig Functions:
“Even” functions behave like polynomials with even
exponents, in that when you change the sign of x, the y
value doesn’t change.
Cosine is an even function because: cos cos
Secant is also an even function, because it is the reciprocal
of cosine.
Even functions are symmetric about the y - axis.
Even and Odd Trig Functions:
“Odd” functions behave like polynomials with odd
exponents, in that when you change the sign of x, the
sign of the y value also changes.
Sine is an odd function because:
sin sin
Cosecant, tangent and cotangent are also odd, because
their formulas contain the sine function.
Odd functions have origin symmetry.
The rules for shifting, stretching, shrinking, and reflecting the
graph of a function apply to trigonometric functions.
Vertical stretch or shrink;
reflection about x-axis
a 1 is a stretch.
Vertical shift
Positive d moves up.
y a f b x c d
Horizontal shift
Horizontal stretch or shrink;
Positive c moves left.
reflection about y-axis
b 1 is a shrink. The horizontal changes happen
in the opposite direction to what
you might expect.
When we apply these rules to sine and cosine, we use some
different terms.
A is the amplitude.
Vertical shift
2p
f x A sin x C D
B
Horizontal shift
B is the period.
B
4
A
3
C
2
D
1
-1
0
-1
2p
y 1.5sin x 1 2
4
1
2
x
3
4
5
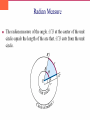
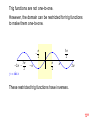
Trig functions are not one-to-one.
However, the domain can be restricted for trig functions
to make them one-to-one.
2p
y sin x
3p
2
p
p
2
p
2
3p
2
p
2p
These restricted trig functions have inverses.
p*