Download Lesson 1: Vectors - Fundamentals and Operations

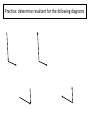
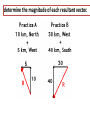
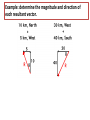
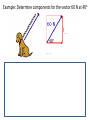
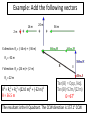
Vectors - Fundamentals and Operations
1.
2.
3.
4.
5.
6.
7.
8.
Vectors and Direction
Vector Addition
Resultants
Vector Components
Vector Resolution
Component Method of Vector Addition
Relative Velocity and Riverboat Problems
Independence of Perpendicular Components of
Motion
Vector vs. scalar quantity
• Vector: a physical quantity that has both a
magnitude and a direction. We use an arrow
above the symbol to represent a vector.

A
• Scalar: a physical quantity that has only a
magnitude but no direction.
A
Representing Vectors
• Vectors on paper are simply arrows
– Direction represented by the way the ARROW POINTS
– Magnitude represented by the ARROW LENGTH
• Examples of Vectors
– Displacement
– Velocity
– Acceleration
– Force
Magnitude of a Vector
• The magnitude of a vector in a scaled vector
diagram is depicted by the length of the
arrow. The arrow is drawn a precise length in
accordance with a chosen scale.
Directions of Vector
Compass Point
The direction of a vector is often expressed as an angle of
rotation of the vector about its "tail" from east, west,
north, or south
20 meters at 10° south of west
34 meters at 42° east of north
N
W
0°
S
Directions of Vector
Reference Vector
Uses due EAST as the 0 degree reference,
all other angles are measured from that point
20 meters at 190°
34 meters at 48°
90°
0°
180°
270°
Changing Systems
• What is the reference vector angle for a vector
that points 50 degrees east of south?
270° + 50° = 320°
50°
• What is the reference vector angle for a vector
that points 20 degrees north of east?
20°
20°
What we can DO with vectors
• ADD/SUBTRACT with a vector
– To produce a NEW VECTOR (RESULTANT)
• MULTIPLY/DIVIDE by a vector or a scalar
– To produce a NEW VECTOR or SCALAR
Vector Addition
• Two vectors can be added together to determine the
result (or resultant). The resultant is the vector sum of
two or more vectors. It is the result of adding two or
more vectors together.
1. Graphical method: using
a scaled vector diagram


A
= ?
• The head-to-tail
+ B
method (tip to tail)
• Parallelogram method
2. Mathematical method Pythagorean theorem and
trigonometric methods
Graphical method 1: head-to-tail
• You are walking north 3 meters, then walking east 4
meters. What is your final displacement?

A

A
+
+

B

B
= ?
  
C  A B
The resultant is from the first tail
to the last head.
Head-to-tail vector addition
Resultant
  
C  A B
applying the head-to-tail method to determine the
sum of two or more vectors:
1. Choose a scale and indicate it on a sheet of paper. The best
choice of scale is one that will result in a diagram that is as
large as possible, yet fits on the sheet of paper.
2. Pick a starting location and draw the first vector to scale in the
indicated direction. Label the magnitude and direction of the
scale on the diagram (e.g., SCALE: 1 cm = 20 m).
3. Starting from where the head of the first vector ends, draw
the tail of second vector to scale in the indicated direction.
Label the magnitude and direction of this vector on the
diagram.
4. Repeat steps 2 and 3 for all vectors that are to be added
5. Draw the resultant from the tail of the first vector to the head
of the last vector. Label this vector as Resultant or simply R.
6. Using a ruler, measure the length of the resultant and
determine its magnitude by converting to real units using the
scale (4.4 cm x 20 m/1 cm = 88 m).
7. Measure the direction of the resultant using the
counterclockwise convention.
practice
• Add following vectors using head and tail
method to determine the resultant, use a
ruler and a protractor.
1. 3 m east, and 4 m south.
2. 5 m north and 12 meters west.
3. 2 m east, 4 m north and 5 m west.
Graphical method 2: parallelogram (tail-tail)
• A cart is pushed in two directions, as the result, the
cart will move in the resultant direction

A

A
+

B
= ?
  
C  A B
+

B

A

B
The resultant is diagonal of the parallelogram from the tail
of both vectors.
Parallelogram vs. head-to-tail

A
+

B
Parallelogram (tail-tail)

A
= ?
Head-to-tail (tip-to-tail)

A

B

B
Parallelogram: tail and tail
touching, the resultant is the
diagonal.
Head-to-tail: head and tail touching,
the resultant is from first tail to last
head.
example
• A model airplane heads due east at 1.50 meters per second,
while the wind blows due north at 0.70 meter per second.
1. Draw the resultant vector in the diagram
2. Determine the scale used in the diagram.
3. Determine, to the nearest degree, the angle between north
and the resultant velocity.
0.7 m/s
θ=?
R
1.5 m/s
θ = 65o
Vector properties
1. Vector can be moved parallel to themselves in a diagram.
 
A B
parallelogram

B
Head-to-tail

A
2. Vectors can be added in any order (commutative and
   
associative)

A B  B  A

B

A
A
B
3. To subtract a vector, add its opposite.

B

A
  

A  B  A  ( B)
4. Multiplying or dividing vectors by scalars results in vectors
with different size, but same direction.
Equilibrant
• The equilibrant vectors of the resultant of A
and B is the opposite of the resultant of
vectors A and B.
B
• Example:
A
Determine
equilibrant of A & B
B
A
Head to tail
R
A
B
R
Parallelogram
Commutative property of vectors
what is the title of this animation:?
Vector subtraction
A
-
=
B
= A
=
A-B
?
+
(-B)
+
Practice: determine resultant for the following diagrams
Mathematical Method - Use
Pythagorean Theorem to determine
magnitude
• The procedure is
restricted to the
addition of two vectors
that make right angles
to each other.

B

A
+

B
A2 + B2 = C2

= A

C
determine the magnitude of each resultant vector.
Mathematical Method - Using
Trigonometry to Determine a
Vector's Direction
Opp.
sin  
Hyp.
Adj.
cos  
Hyp.
Opp.
tan  
Adj.
SOH
CAH
TOA
Example
• Example: Eric leaves the base camp and hikes 11 km, north
and then hikes 11 km east. Determine Eric's resulting
displacement.
θ
A2 + B2 = C2
(11 km)2 + (11 km) 2 = C2
C = 15.6 km
Opp. 11 km
tan  

1
Adj. 11 km
  45o
Eric’s displacement is 15.6 km at 45o northeast
• Note: The measure of an angle as determined through use of
SOH CAH TOA is not always the direction of the vector.
Example: determine the magnitude and direction of
each resultant vector.
Vector Addition: 6 + 8 = ?
All that can be said for certain is that 8 + 6 can add up to a vector
with a maximum magnitude of 14 and a minimum magnitude of 2.
The maximum is obtained when the two vectors are directed in the
same direction. The minimum is obtained when the two vectors are
directed in the opposite direction. The sum of vectors 8 and vector 6
can be any number between 14 and 2.
Example
•
1.
2.
3.
4.
A 5.0-newton force and a 7.0-newton force
act concurrently on a point. As the angle
between the forces is increased from 0° to
180°, the magnitude of the resultant of the
two forces changes from
0.0 N to 12.0 N
2.0 N to 12.0 N
12.0 N to 2.0 N
12.0 N to 0.0 N
Example
•
1.
2.
3.
4.
A 3-newton force and a 4-newton force are
acting concurrently on a point. Which force
could not produce equilibrium with these two
forces?
1N
7N
9N
4N
Example
•
As the angle between two concurrent forces
decreases, the magnitude of the force
required to produce equilibrium
1. decreases
2. increases
3. remains the same
Example
• Two 20.-newton forces act concurrently on an
object. What angle between these forces will
produce a resultant force with the greatest
magnitude?
A. 0°
B. 45°
C. 90.°
D. 180.°
practices
1.
A person walks 150. meters due east and then walks 30. meters due west.
The entire trip takes the person 10. minutes. Determine the magnitude and
the direction of the person’s total displacement.
2. A dog walks 8.0 meters due north and then 6.0 meters due east.
a. Determine the magnitude of the dog’s total displacement.
b. Use appropriate scale to draw a vector diagram including the resultant
based on the information given.
3. A 20.-newton force due north and a 20.-newton force due east act
concurrently on an object. What is the additional force necessary to bring
the object into a state of equilibrium?
4. As the angle between two concurrent forces decreases, what happens to
the magnitude of the force required to produce equilibrium?
Vector Components
• In situations in which vectors are directed at angles to the
customary coordinate axes, we transform the vector into two
parts with each part being directed along the coordinate axes.
Each part is called a component of the vector. So any vector
can be transformed into two components.
Component 1
Component 1
Component 2
Component 2
• Any vector directed in two dimensions can be thought of as
having an influence in two different directions.
• Each part of a two-dimensional vector is known as a component.
• The components of a vector depict the influence of that vector in
a given direction.
• The combined influence of the two components is equivalent to
the influence of the single two-dimensional vector.
• The single two-dimensional vector could be replaced by the two
components.
Finding components –
Vector Resolution
•
To determine the magnitudes of the
components of a vector, we the
trigonometric method
Opp. Ay
sin  

Hyp. A
Ay  A sin 
y

A
Ay
θ
Ax
x
Adj. Ax
cos  

Hyp. A
Ax  A cos 
Trigonometric Method of Vector
Resolution
1. Construct a rough sketch (no scale needed) of the vector
in the indicated direction. Draw a rectangle about the
vector such that the vector is the diagonal of the
rectangle.
2. Label the components of the vectors with symbols to
indicate which component represents which side.
3. To determine the length of the side opposite the
indicated angle, use the sine function. Substitute the
magnitude of the vector for the length of the hypotenuse.
4. Repeat the above step using the cosine function to
determine the length of the side adjacent to the indicated
angle.
Example: Determine components for the vector 60 N at 40o
Example
• The vector diagram below represents the horizontal
component, FH, and the vertical component, FV, of a 24newton force acting at 35° above the horizontal.
• What are the magnitudes of the horizontal and vertical
components?
practices
1.
2.
3.
4.
5.
A baseball is thrown at an angle of 40.0° above the horizontal. The
horizontal component of the baseball’s initial velocity is 12.0 meters per
second. What is the magnitude of the ball’s initial velocity?
An airplane flies with a velocity of 750. kilometers per hour, 30.0° south
of east. What is the magnitude of the eastward component of the plane’s
velocity?
A vector makes an angle, θ, with the horizontal. What is θ if the
horizontal and vertical components of the vector are equal in magnitude?
A person exerting a 300.-newton force on the handle of a shovel that
makes an angle of 60.° with the horizontal ground. What is the
component of the 300.-newton force that acts perpendicular to the
ground?
As the angle between a force and level ground decreases from 60° to 30°,
what happens to the the vertical component of the force?
Component Method of
Vector Addition
• In order to solve more complex vector addition problems, we
need to combine the concept of vector components and the
principles of vector resolution with the use of the
Pythagorean theorem.
Addition of Three or More
Right Angle Vectors
• Add horizontal
components
• Add vertical
components
R2 = (8.0 km)2 + (6.0 km)2
R2 = 64.0 km2+ 36.0 km2
R2 = 100.0 km2
R = SQRT (100.0 km2)
R = 10.0 km
Use Tangent Function (TOA) to find
Direction of Vectors
Tangent(Θ) = Opposite/Adjacent
Tangent(Θ) = 8.0/6.0
Θ =53°
• Since the angle that the resultant makes with
east is the complement of the angle that it
makes with north, we could express the
direction as 53° CCW.
Example: Add the following vectors
16 m
24 m
36 m
2m
X direction: Rx = (-16 m) + (-36 m)
Rx = -52 m
Y direction: Ry = (24 m) + (-2 m)
Ry = 22 m
R2 = Rx2 + Ry2 =(22.0 m)2 + (-52 m)2
R = 56.5 m
Θ
Tan(Θ) = Opp./Adj.
Tan(Θ)=52m/(22m)
Θ =67°
The resultant is the II Quadrant. The CCW direction is 157.1° CCW.
Adding vectors that are not
perpendicular
Add the components of the original displacement vectors to find
two components that form a right triangle with the resultant
vector.
Adding vectors algebraically
1. Find the x and y components of all vectors.
Ax=AcosθA;
Ay=AsinθA;
Bx=BcosθB;
By=BsinθB
2. Find the x and y component of the resultant vector:
Rx=Ax + Bx;
Ry=Ay + By
3. Use the Pythagorean theorem to find the magnitude of the
resultant vector.
2
2
R  Rx  R y
4. Use tan-1 function to find the angle the resultant vector
makes with the x-axis.
Ry
1
 R  tan ( )
Rx
5. Evaluate your answer.
Example
• A hiker walks 25.5 km from her base camp at 35o south of
east. On the second day, she walks 41.0 km in a direction 65o
north of east at which point she discovers a forest ranger’s
tower. Determine the magnitude and direction of her
resultant displacement between the base camp and the
ranger’s tower.
R
d2
35o
d1
65o
Example
A bus heads 6.00 km east, then 3.5 km north, then 1.50
km at 45o south of west. What is the total displacement?
A: 6.0 km, 0° CCW
B: 3.5 km, 90° CCW
C: 1.5 km, 225° CCW
+
A
+
B
C
Cx = Ccos225o = -1.06 km
Cy = Csin225o = - 1.06 km
Example
• Cameron and Baxter are on a hike. Starting from home base,
they make the following movements.
A: 2.65 km, 140° CCW
B: 4.77 km, 252° CCW
C: 3.18 km, 332° CCW
• Determine the magnitude and direction of their overall
displacement.
Vector
X Component (km)
Y Component
A
2.65 km
140° CCW
(2.65 km)•cos(140°) (2.65 km)•sin(140°)
= -2.030
= 1.703
B
4.77 km
252° CCW
(4.77 km)•cos(252°) (4.77 km)•sin(252°)
= -1.474
= -4.536
C
3.18 km
332° CCW
(3.18 km)•cos(332°) (3.18 km)•sin(332°)
= 2.808
= -1.493
Sum of
A+B+C
-0.696
R = 4.38 km
-4.326
Θ = 80.9°
Direction is at 260.9° (CCW)
Relative Velocity and Riverboat
Problems
When objects move within a medium that is also moving with respect
to an observer, the resultant velocity can be determined by vector
addition.
Analysis of a Riverboat's Motion
• The affect of the wind upon the plane is similar to the affect
of the river current upon the motorboat.
Example
Suppose that the river was moving with a velocity of 3 m/s,
North and the motorboat was moving with a velocity of 4 m/s,
East.
1. What is the resultant velocity (both magnitude and
direction) of the boat?
2. If the width of the river is 500 meters wide, then how
much time does it take the boat to travel shore to shore?
3. What distance downstream does the boat reach the
opposite shore?
To calculate resultant velocity
A2+B2 = R2
(4.0 m/s)2 + (3.0 m/s)2 = R2
16 m2/s2 + 9 m2/s2 = R2
25 m2/s2 = R2
SQRT (25 m2/s2) = R
5.0 m/s = R
tan(θ) = (opposite/adjacent)
tan(θ) = (3/4)
θ = tan-1 (3/4)
θ = 36.9o
To calculate time
Critical variable in multi dimensional problems is TIME.
We must consider each dimension SEPARATELY, using TIME as
the only crossover VARIABLE.
d
v
t
d
t
v
d 500 m
t 
 125 s
v 4 m/s
d and v must be in the same dimension
To calculate distance downstream
Critical variable in multi dimensional problems is TIME.
We must consider each dimension SEPARATELY, using TIME as
the only crossover VARIABLE.
d
v
t
d  v t
d and v must be in the same dimension
d  (3 m / s)(125 s)  375 m
Example 1
•
A motorboat traveling 12 m/s, East
encounters a current traveling 5.0 m/s,
North.
1. What is the resultant velocity of the motorboat?
2. If the width of the river is 96 meters wide, then
how much time does it take the boat to travel
shore to shore?
3. What distance downstream does the boat reach
the opposite shore?
Example 2
•
1.
2.
3.
A motorboat traveling 4 m/s, East encounters a current
traveling 7.0 m/s, North.
What is the resultant velocity of the motorboat?
If the width of the river is 80 meters wide, then how much time
does it take the boat to travel shore to shore?
What distance downstream does the boat reach the opposite
shore?
Example 3
• A stream is 30. meters wide and its current flows southward
at 1.5 meters per second. A toy boat is launched with a
velocity of 2.0 meters per second eastward from the west
bank of the stream.
1. What is the magnitude of the boat’s resultant velocity as it
crosses the stream?
2. How much time does it take the toy boat to travel shore to
shore?
3. What distance downstream does the toy boat reach the
opposite shore?
Independence of Perpendicular
Components of Motion
• In the riverboat or airplane problems, the resultant
velocity is obtained by adding the perpendicular
components. These perpendicular components are
independent of each other, which means, as one
changes, the other is not affected at all. For
example, it does not matter with what speed I launch
the toy boat, the speed of the river remains the
same, even though the resultant velocity changes.
Extra credit question
•
Mia Ander exits the front door of her home and walks along
the path shown in the diagram at the right (not to scale). The
walk consists of four legs with the following magnitudes:
A = 46 m
B = 142 m
C = 78 m
D = 89 m
•
Determine the magnitude and direction of Mia's resultant
displacement. Consider using a table to organize your
calculations.