* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Lesson 1: Vectors - Fundamentals and Operations
Derivations of the Lorentz transformations wikipedia , lookup
Probability amplitude wikipedia , lookup
Cauchy stress tensor wikipedia , lookup
Dynamical system wikipedia , lookup
Fictitious force wikipedia , lookup
Hooke's law wikipedia , lookup
Symmetry in quantum mechanics wikipedia , lookup
Photon polarization wikipedia , lookup
Minkowski space wikipedia , lookup
Tensor operator wikipedia , lookup
Velocity-addition formula wikipedia , lookup
Relativistic angular momentum wikipedia , lookup
Classical central-force problem wikipedia , lookup
Work (physics) wikipedia , lookup
Bra–ket notation wikipedia , lookup
Rigid body dynamics wikipedia , lookup
Laplace–Runge–Lenz vector wikipedia , lookup
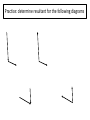
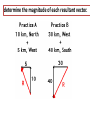
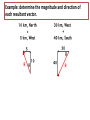
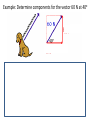
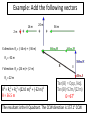
Vectors - Fundamentals and Operations 1. 2. 3. 4. 5. 6. 7. 8. Vectors and Direction Vector Addition Resultants Vector Components Vector Resolution Component Method of Vector Addition Relative Velocity and Riverboat Problems Independence of Perpendicular Components of Motion Vector vs. scalar quantity • Vector: a physical quantity that has both a magnitude and a direction. We use an arrow above the symbol to represent a vector. A • Scalar: a physical quantity that has only a magnitude but no direction. A Representing Vectors • Vectors on paper are simply arrows – Direction represented by the way the ARROW POINTS – Magnitude represented by the ARROW LENGTH • Examples of Vectors – Displacement – Velocity – Acceleration – Force Magnitude of a Vector • The magnitude of a vector in a scaled vector diagram is depicted by the length of the arrow. The arrow is drawn a precise length in accordance with a chosen scale. Directions of Vector Compass Point The direction of a vector is often expressed as an angle of rotation of the vector about its "tail" from east, west, north, or south 20 meters at 10° south of west 34 meters at 42° east of north N W 0° S Directions of Vector Reference Vector Uses due EAST as the 0 degree reference, all other angles are measured from that point 20 meters at 190° 34 meters at 48° 90° 0° 180° 270° Changing Systems • What is the reference vector angle for a vector that points 50 degrees east of south? 270° + 50° = 320° 50° • What is the reference vector angle for a vector that points 20 degrees north of east? 20° 20° What we can DO with vectors • ADD/SUBTRACT with a vector – To produce a NEW VECTOR (RESULTANT) • MULTIPLY/DIVIDE by a vector or a scalar – To produce a NEW VECTOR or SCALAR Vector Addition • Two vectors can be added together to determine the result (or resultant). The resultant is the vector sum of two or more vectors. It is the result of adding two or more vectors together. 1. Graphical method: using a scaled vector diagram A = ? • The head-to-tail + B method (tip to tail) • Parallelogram method 2. Mathematical method Pythagorean theorem and trigonometric methods Graphical method 1: head-to-tail • You are walking north 3 meters, then walking east 4 meters. What is your final displacement? A A + + B B = ? C A B The resultant is from the first tail to the last head. Head-to-tail vector addition Resultant C A B applying the head-to-tail method to determine the sum of two or more vectors: 1. Choose a scale and indicate it on a sheet of paper. The best choice of scale is one that will result in a diagram that is as large as possible, yet fits on the sheet of paper. 2. Pick a starting location and draw the first vector to scale in the indicated direction. Label the magnitude and direction of the scale on the diagram (e.g., SCALE: 1 cm = 20 m). 3. Starting from where the head of the first vector ends, draw the tail of second vector to scale in the indicated direction. Label the magnitude and direction of this vector on the diagram. 4. Repeat steps 2 and 3 for all vectors that are to be added 5. Draw the resultant from the tail of the first vector to the head of the last vector. Label this vector as Resultant or simply R. 6. Using a ruler, measure the length of the resultant and determine its magnitude by converting to real units using the scale (4.4 cm x 20 m/1 cm = 88 m). 7. Measure the direction of the resultant using the counterclockwise convention. practice • Add following vectors using head and tail method to determine the resultant, use a ruler and a protractor. 1. 3 m east, and 4 m south. 2. 5 m north and 12 meters west. 3. 2 m east, 4 m north and 5 m west. Graphical method 2: parallelogram (tail-tail) • A cart is pushed in two directions, as the result, the cart will move in the resultant direction A A + B = ? C A B + B A B The resultant is diagonal of the parallelogram from the tail of both vectors. Parallelogram vs. head-to-tail A + B Parallelogram (tail-tail) A = ? Head-to-tail (tip-to-tail) A B B Parallelogram: tail and tail touching, the resultant is the diagonal. Head-to-tail: head and tail touching, the resultant is from first tail to last head. example • A model airplane heads due east at 1.50 meters per second, while the wind blows due north at 0.70 meter per second. 1. Draw the resultant vector in the diagram 2. Determine the scale used in the diagram. 3. Determine, to the nearest degree, the angle between north and the resultant velocity. 0.7 m/s θ=? R 1.5 m/s θ = 65o Vector properties 1. Vector can be moved parallel to themselves in a diagram. A B parallelogram B Head-to-tail A 2. Vectors can be added in any order (commutative and associative) A B B A B A A B 3. To subtract a vector, add its opposite. B A A B A ( B) 4. Multiplying or dividing vectors by scalars results in vectors with different size, but same direction. Equilibrant • The equilibrant vectors of the resultant of A and B is the opposite of the resultant of vectors A and B. B • Example: A Determine equilibrant of A & B B A Head to tail R A B R Parallelogram Commutative property of vectors what is the title of this animation:? Vector subtraction A - = B = A = A-B ? + (-B) + Practice: determine resultant for the following diagrams Mathematical Method - Use Pythagorean Theorem to determine magnitude • The procedure is restricted to the addition of two vectors that make right angles to each other. B A + B A2 + B2 = C2 = A C determine the magnitude of each resultant vector. Mathematical Method - Using Trigonometry to Determine a Vector's Direction Opp. sin Hyp. Adj. cos Hyp. Opp. tan Adj. SOH CAH TOA Example • Example: Eric leaves the base camp and hikes 11 km, north and then hikes 11 km east. Determine Eric's resulting displacement. θ A2 + B2 = C2 (11 km)2 + (11 km) 2 = C2 C = 15.6 km Opp. 11 km tan 1 Adj. 11 km 45o Eric’s displacement is 15.6 km at 45o northeast • Note: The measure of an angle as determined through use of SOH CAH TOA is not always the direction of the vector. Example: determine the magnitude and direction of each resultant vector. Vector Addition: 6 + 8 = ? All that can be said for certain is that 8 + 6 can add up to a vector with a maximum magnitude of 14 and a minimum magnitude of 2. The maximum is obtained when the two vectors are directed in the same direction. The minimum is obtained when the two vectors are directed in the opposite direction. The sum of vectors 8 and vector 6 can be any number between 14 and 2. Example • 1. 2. 3. 4. A 5.0-newton force and a 7.0-newton force act concurrently on a point. As the angle between the forces is increased from 0° to 180°, the magnitude of the resultant of the two forces changes from 0.0 N to 12.0 N 2.0 N to 12.0 N 12.0 N to 2.0 N 12.0 N to 0.0 N Example • 1. 2. 3. 4. A 3-newton force and a 4-newton force are acting concurrently on a point. Which force could not produce equilibrium with these two forces? 1N 7N 9N 4N Example • As the angle between two concurrent forces decreases, the magnitude of the force required to produce equilibrium 1. decreases 2. increases 3. remains the same Example • Two 20.-newton forces act concurrently on an object. What angle between these forces will produce a resultant force with the greatest magnitude? A. 0° B. 45° C. 90.° D. 180.° practices 1. A person walks 150. meters due east and then walks 30. meters due west. The entire trip takes the person 10. minutes. Determine the magnitude and the direction of the person’s total displacement. 2. A dog walks 8.0 meters due north and then 6.0 meters due east. a. Determine the magnitude of the dog’s total displacement. b. Use appropriate scale to draw a vector diagram including the resultant based on the information given. 3. A 20.-newton force due north and a 20.-newton force due east act concurrently on an object. What is the additional force necessary to bring the object into a state of equilibrium? 4. As the angle between two concurrent forces decreases, what happens to the magnitude of the force required to produce equilibrium? Vector Components • In situations in which vectors are directed at angles to the customary coordinate axes, we transform the vector into two parts with each part being directed along the coordinate axes. Each part is called a component of the vector. So any vector can be transformed into two components. Component 1 Component 1 Component 2 Component 2 • Any vector directed in two dimensions can be thought of as having an influence in two different directions. • Each part of a two-dimensional vector is known as a component. • The components of a vector depict the influence of that vector in a given direction. • The combined influence of the two components is equivalent to the influence of the single two-dimensional vector. • The single two-dimensional vector could be replaced by the two components. Finding components – Vector Resolution • To determine the magnitudes of the components of a vector, we the trigonometric method Opp. Ay sin Hyp. A Ay A sin y A Ay θ Ax x Adj. Ax cos Hyp. A Ax A cos Trigonometric Method of Vector Resolution 1. Construct a rough sketch (no scale needed) of the vector in the indicated direction. Draw a rectangle about the vector such that the vector is the diagonal of the rectangle. 2. Label the components of the vectors with symbols to indicate which component represents which side. 3. To determine the length of the side opposite the indicated angle, use the sine function. Substitute the magnitude of the vector for the length of the hypotenuse. 4. Repeat the above step using the cosine function to determine the length of the side adjacent to the indicated angle. Example: Determine components for the vector 60 N at 40o Example • The vector diagram below represents the horizontal component, FH, and the vertical component, FV, of a 24newton force acting at 35° above the horizontal. • What are the magnitudes of the horizontal and vertical components? practices 1. 2. 3. 4. 5. A baseball is thrown at an angle of 40.0° above the horizontal. The horizontal component of the baseball’s initial velocity is 12.0 meters per second. What is the magnitude of the ball’s initial velocity? An airplane flies with a velocity of 750. kilometers per hour, 30.0° south of east. What is the magnitude of the eastward component of the plane’s velocity? A vector makes an angle, θ, with the horizontal. What is θ if the horizontal and vertical components of the vector are equal in magnitude? A person exerting a 300.-newton force on the handle of a shovel that makes an angle of 60.° with the horizontal ground. What is the component of the 300.-newton force that acts perpendicular to the ground? As the angle between a force and level ground decreases from 60° to 30°, what happens to the the vertical component of the force? Component Method of Vector Addition • In order to solve more complex vector addition problems, we need to combine the concept of vector components and the principles of vector resolution with the use of the Pythagorean theorem. Addition of Three or More Right Angle Vectors • Add horizontal components • Add vertical components R2 = (8.0 km)2 + (6.0 km)2 R2 = 64.0 km2+ 36.0 km2 R2 = 100.0 km2 R = SQRT (100.0 km2) R = 10.0 km Use Tangent Function (TOA) to find Direction of Vectors Tangent(Θ) = Opposite/Adjacent Tangent(Θ) = 8.0/6.0 Θ =53° • Since the angle that the resultant makes with east is the complement of the angle that it makes with north, we could express the direction as 53° CCW. Example: Add the following vectors 16 m 24 m 36 m 2m X direction: Rx = (-16 m) + (-36 m) Rx = -52 m Y direction: Ry = (24 m) + (-2 m) Ry = 22 m R2 = Rx2 + Ry2 =(22.0 m)2 + (-52 m)2 R = 56.5 m Θ Tan(Θ) = Opp./Adj. Tan(Θ)=52m/(22m) Θ =67° The resultant is the II Quadrant. The CCW direction is 157.1° CCW. Adding vectors that are not perpendicular Add the components of the original displacement vectors to find two components that form a right triangle with the resultant vector. Adding vectors algebraically 1. Find the x and y components of all vectors. Ax=AcosθA; Ay=AsinθA; Bx=BcosθB; By=BsinθB 2. Find the x and y component of the resultant vector: Rx=Ax + Bx; Ry=Ay + By 3. Use the Pythagorean theorem to find the magnitude of the resultant vector. 2 2 R Rx R y 4. Use tan-1 function to find the angle the resultant vector makes with the x-axis. Ry 1 R tan ( ) Rx 5. Evaluate your answer. Example • A hiker walks 25.5 km from her base camp at 35o south of east. On the second day, she walks 41.0 km in a direction 65o north of east at which point she discovers a forest ranger’s tower. Determine the magnitude and direction of her resultant displacement between the base camp and the ranger’s tower. R d2 35o d1 65o Example A bus heads 6.00 km east, then 3.5 km north, then 1.50 km at 45o south of west. What is the total displacement? A: 6.0 km, 0° CCW B: 3.5 km, 90° CCW C: 1.5 km, 225° CCW + A + B C Cx = Ccos225o = -1.06 km Cy = Csin225o = - 1.06 km Example • Cameron and Baxter are on a hike. Starting from home base, they make the following movements. A: 2.65 km, 140° CCW B: 4.77 km, 252° CCW C: 3.18 km, 332° CCW • Determine the magnitude and direction of their overall displacement. Vector X Component (km) Y Component A 2.65 km 140° CCW (2.65 km)•cos(140°) (2.65 km)•sin(140°) = -2.030 = 1.703 B 4.77 km 252° CCW (4.77 km)•cos(252°) (4.77 km)•sin(252°) = -1.474 = -4.536 C 3.18 km 332° CCW (3.18 km)•cos(332°) (3.18 km)•sin(332°) = 2.808 = -1.493 Sum of A+B+C -0.696 R = 4.38 km -4.326 Θ = 80.9° Direction is at 260.9° (CCW) Relative Velocity and Riverboat Problems When objects move within a medium that is also moving with respect to an observer, the resultant velocity can be determined by vector addition. Analysis of a Riverboat's Motion • The affect of the wind upon the plane is similar to the affect of the river current upon the motorboat. Example Suppose that the river was moving with a velocity of 3 m/s, North and the motorboat was moving with a velocity of 4 m/s, East. 1. What is the resultant velocity (both magnitude and direction) of the boat? 2. If the width of the river is 500 meters wide, then how much time does it take the boat to travel shore to shore? 3. What distance downstream does the boat reach the opposite shore? To calculate resultant velocity A2+B2 = R2 (4.0 m/s)2 + (3.0 m/s)2 = R2 16 m2/s2 + 9 m2/s2 = R2 25 m2/s2 = R2 SQRT (25 m2/s2) = R 5.0 m/s = R tan(θ) = (opposite/adjacent) tan(θ) = (3/4) θ = tan-1 (3/4) θ = 36.9o To calculate time Critical variable in multi dimensional problems is TIME. We must consider each dimension SEPARATELY, using TIME as the only crossover VARIABLE. d v t d t v d 500 m t 125 s v 4 m/s d and v must be in the same dimension To calculate distance downstream Critical variable in multi dimensional problems is TIME. We must consider each dimension SEPARATELY, using TIME as the only crossover VARIABLE. d v t d v t d and v must be in the same dimension d (3 m / s)(125 s) 375 m Example 1 • A motorboat traveling 12 m/s, East encounters a current traveling 5.0 m/s, North. 1. What is the resultant velocity of the motorboat? 2. If the width of the river is 96 meters wide, then how much time does it take the boat to travel shore to shore? 3. What distance downstream does the boat reach the opposite shore? Example 2 • 1. 2. 3. A motorboat traveling 4 m/s, East encounters a current traveling 7.0 m/s, North. What is the resultant velocity of the motorboat? If the width of the river is 80 meters wide, then how much time does it take the boat to travel shore to shore? What distance downstream does the boat reach the opposite shore? Example 3 • A stream is 30. meters wide and its current flows southward at 1.5 meters per second. A toy boat is launched with a velocity of 2.0 meters per second eastward from the west bank of the stream. 1. What is the magnitude of the boat’s resultant velocity as it crosses the stream? 2. How much time does it take the toy boat to travel shore to shore? 3. What distance downstream does the toy boat reach the opposite shore? Independence of Perpendicular Components of Motion • In the riverboat or airplane problems, the resultant velocity is obtained by adding the perpendicular components. These perpendicular components are independent of each other, which means, as one changes, the other is not affected at all. For example, it does not matter with what speed I launch the toy boat, the speed of the river remains the same, even though the resultant velocity changes. Extra credit question • Mia Ander exits the front door of her home and walks along the path shown in the diagram at the right (not to scale). The walk consists of four legs with the following magnitudes: A = 46 m B = 142 m C = 78 m D = 89 m • Determine the magnitude and direction of Mia's resultant displacement. Consider using a table to organize your calculations.