Download Document

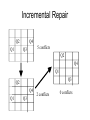
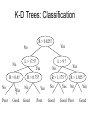
Searching by Constraint
(Continued)
CMSC 25000
Artificial Intelligence
January 29, 2008
Incremental Repair
• Start with initial complete assignment
– Use greedy approach
– Probably invalid - I.e. violates some
constraints
• Incrementally convert to valid solution
– Use heuristic to replace value that violates
– “min-conflict” strategy:
• Change value to result in fewest constraint
violations
• Break ties randomly
• Incorporate in local or backtracking hill-climber
Incremental Repair
Q2
Q1
Q4
5 conflicts
Q3
Q2
Q4
Q1
Q3
Q2
Q4
Q1
Q3
2 conflicts
0 conflicts
Question
• How would we apply iterative repair to
Traveling Salesman Problem?
Iterative Improvement
• Alternate formulation of CSP
– Rather than DFS through partial assignments
– Start with some complete, valid assignment
• Search for optimal assignment wrt some criterion
• Example: Traveling Salesman Problem
– Minimum length tour through cities, visiting
each one once
Iterative Improvement Example
• TSP
– Start with some valid tour
• E.g. find greedy solution
– Make incremental change to tour
• E.g. hill-climbing - take change that produces
greatest improvement
– Problem: Local minima
– Solution: Randomize to search other parts of space
• Other methods: Simulated annealing, Genetic alg’s
Min-Conflict Effectiveness
• N-queens: Given initial random assignment,
can solve in ~ O(n)
– For n < 10^7
• GSAT (satisfiability)
– Best (near linear in practice) solution uses minconflict-type hill-climbing strategy
• Adds randomization to escape local min
• ~Linear seems true for most CSPs
– Except for some range of ratios of constraints to
variables
• Avoids storage of assignment history (for BT)
Evolutionary Search
Artificial Intelligence
CMSC 25000
January 29, 2008
Agenda
• Motivation:
– Evolving a solution
• Genetic Algorithms
– Modelling search as evolution
•
•
•
•
Mutation
Crossover
Survival of the fittest
Survival of the most diverse
• Conclusions
Motivation: Evolution
• Evolution through natural selection
– Individuals pass on traits to offspring
– Individuals have different traits
– Fittest individuals survive to produce more
offspring
– Over time, variation can accumulate
• Leading to new species
Simulated Evolution
• Evolving a solution
• Begin with population of individuals
– Individuals = candidate solutions ~chromosomes
• Produce offspring with variation
– Mutation: change features
– Crossover: exchange features between individuals
• Apply natural selection
– Select “best” individuals to go on to next generation
• Continue until satisfied with solution
Genetic Algorithms Applications
• Search parameter space for optimal
assignment
– Not guaranteed to find optimal, but can approach
• Classic optimization problems:
– E.g. Travelling Salesman Problem
• Program design (“Genetic Programming”)
• Aircraft carrier landings
Genetic Algorithm Example
• Cookie recipes (Winston, AI, 1993)
• As evolving populations
• Individual = batch of cookies
• Quality: 0-9
– Chromosomes = 2 genes: 1 chromosome each
• Flour Quantity, Sugar Quantity: 1-9
• Mutation:
– Randomly select Flour/Sugar: +/- 1 [1-9]
• Crossover:
– Split 2 chromosomes & rejoin; keeping both
Fitness
• Natural selection: Most fit survive
• Fitness= Probability of survival to next gen
• Question: How do we measure fitness?
– “Standard method”: Relate fitness to quality
•
f i :0-1; qi
:1-9:
fi  qi /  q j
j
Chromosome
Quality
Fitness
14
31
12
11
4
3
2
1
0.4
0.3
0.2
0.1
GA Design Issues
• Genetic design:
– Identify sets of features = genes; Constraints?
• Population: How many chromosomes?
– Too few => inbreeding; Too many=>too slow
• Mutation: How frequent?
– Too few=>slow change; Too many=> wild
• Crossover: Allowed? How selected?
• Duplicates?
GA Design: Basic Cookie GA
• Genetic design:
– Identify sets of features: 2 genes:
flour+sugar;1-9
• Population: How many chromosomes?
– 1 initial, 4 max
• Mutation: How frequent?
– 1 gene randomly selected, randomly mutated
• Crossover: Allowed? No
• Duplicates? No
• Survival: Standard method
Basic Cookie GA Results
• Results are for 1000 random trials
– Initial state: 1 1-1, quality 1 chromosome
• On average, reaches max quality (9) in
16 generations
• Best: max quality in 8 generations
• Conclusion:
– Low dimensionality search
• Successful even without crossover
Basic Cookie GA+Crossover
Results
• Results are for 1000 random trials
– Initial state: 1 1-1, quality 1 chromosome
• On average, reaches max quality (9) in 14
generations
• Conclusion:
– Faster with crossover: combine good in each gene
– Key: Global max achievable by maximizing each
dimension independently - reduce dimensionality
Solving the Moat Problem
• Problem:
– No single step mutation
can reach optimal values
using standard fitness
(quality=0 =>
probability=0)
• Solution A:
– Crossover can combine fit
parents in EACH gene
• However, still slow: 155
generations on average
1
2
3
4
5
4
3
2
1
2
0
0
0
0
0
0
0
2
3
0
0
0
0
0
0
0
3
4
0
0
7
8
7
0
0
4
5
0
0
8
9
8
0
0
5
4
0
0
7
8
7
0
0
4
3
0
0
0
0
0
0
0
3
2
0
0
0
0
0
0
0
2
1
2
3
4
5
4
3
2
1
Questions
• How can we avoid the 0 quality problem?
• How can we avoid local maxima?
Rethinking Fitness
• Goal: Explicit bias to best
– Remove implicit biases based on quality
scale
• Solution: Rank method
– Ignore actual quality values except for ranking
• Step 1: Rank candidates by quality
• Step 2: Probability of selecting ith candidate, given
that i-1 candidate not selected, is constant p.
– Step 2b: Last candidate is selected if no other has been
• Step 3: Select candidates using the probabilities
Rank Method
Chromosome
14
13
12
52
75
Quality Rank Std. Fitness Rank Fitness
4
3
2
1
0
1
2
3
4
5
0.4
0.3
0.2
0.1
0.0
0.667
0.222
0.074
0.025
0.012
Results: Average over 1000 random runs on Moat problem
- 75 Generations (vs 155 for standard method)
No 0 probability entries: Based on rank not absolute quality
Diversity
• Diversity:
– Degree to which chromosomes exhibit
different genes
– Rank & Standard methods look only at quality
– Need diversity: escape local min, variety for
crossover
– “As good to be different as to be fit”
Rank-Space Method
• Combines diversity and quality in fitness
• Diversity measure:
– Sum of inverse squared distances in genes
1
di

• Diversity rank: Avoids inadvertent bias
• Rank-space:
i
– Sort on sum of diversity AND quality ranks
– Best: lower left: high diversity & quality
Rank-Space Method
W.r.t. highest ranked 5-1
Chromosome
14
31
12
11
75
Q
D
D Rank Q Rank Comb Rank R-S Fitness
4
3
2
1
0
0.04
0.25
0.059
0.062
0.05
1
5
3
4
2
1
2
3
4
5
1
4
2
5
3
Diversity rank breaks ties
After select others, sum distances to both
Results: Average (Moat) 15 generations
0.667
0.025
0.222
0.012
0.074
GA’s and Local Maxima
• Quality metrics only:
– Susceptible to local max problems
• Quality + Diversity:
– Can populate all local maxima
• Including global max
– Key: Population must be large enough
GA Discussion
• Similar to stochastic local beam search
– Beam: Population size
– Stochastic: selection & mutation
– Local: Each generation from single previous
– Key difference: Crossover – 2 sources!
• Why crossover?
– Schema: Partial local subsolutions
• E.g. 2 halves of TSP tour
Question
• Traveling Salesman Problem
– CSP-style Iterative refinement
– Genetic Algorithm
• N-Queens
– CSP-style Iterative refinement
– Genetic Algorithm
Iterative Improvement Example
• TSP
– Start with some valid tour
• E.g. find greedy solution
– Make incremental change to tour
• E.g. hill-climbing - take change that produces
greatest improvement
– Problem: Local minima
– Solution: Randomize to search other parts of space
• Other methods: Simulated annealing, Genetic alg’s
Machine Learning:
Nearest Neighbor &
Information Retrieval Search
Artificial Intelligence
CMSC 25000
January 29, 2008
Agenda
• Machine learning: Introduction
• Nearest neighbor techniques
– Applications:
• Credit rating
• Text Classification
– K-nn
– Issues:
• Distance, dimensions, & irrelevant attributes
• Efficiency:
– k-d trees, parallelism
Machine Learning
• Learning: Acquiring a function, based on
past inputs and values, from new inputs to
values.
• Learn concepts, classifications, values
– Identify regularities in data
Machine Learning Examples
• Pronunciation:
– Spelling of word => sounds
• Speech recognition:
– Acoustic signals => sentences
• Robot arm manipulation:
– Target => torques
• Credit rating:
– Financial data => loan qualification
Complexity & Generalization
• Goal: Predict values accurately on new
inputs
• Problem:
– Train on sample data
– Can make arbitrarily complex model to fit
– BUT, will probably perform badly on NEW data
• Strategy:
– Limit complexity of model (e.g. degree of equ’n)
– Split training and validation sets
• Hold out data to check for overfitting
Nearest Neighbor
• Memory- or case- based learning
• Supervised method: Training
– Record labeled instances and feature-value
vectors
• For each new, unlabeled instance
– Identify “nearest” labeled instance
– Assign same label
• Consistency heuristic: Assume that a
property is the same as that of the nearest
reference case.
Nearest Neighbor Example
• Credit Rating:
– Classifier: Good /
Poor
– Features:
• L = # late payments/yr;
• R = Income/Expenses
Name
L
R
G/P
A
0
1.2
G
B
25
0.4
P
C
D
E
5
20
30
0.7
0.8
0.85
G
P
P
F
G
H
11 1.2
7
1.15
15 0.8
G
G
P
Nearest Neighbor Example
Name
L
R
G/P
A
0
1.2
G
B
25
0.4
P
C
D
E
5 0.7
20 0.8
30 0.85
F
G
H
11 1.2
7
1.15
15 0.8
G
P
P
G
G
P
1 A
R
G
F
H
C
E
D
B
10
L
20
30
Nearest Neighbor Example
Name
L
R
G/P
I
6
1.15
G
J
22
0.45
K
15
1.2
P
??
1 A
R
IG F
K
H
C
E
D
J B
Distance Measure:
Sqrt ((L1-L2)^2 + [sqrt(10)*(R1-R2)]^2))
- Scaled distance
10
L
20
30
Nearest Neighbor Analysis
• Problem:
– Ambiguous labeling, Training Noise
• Solution:
– K-nearest neighbors
• Not just single nearest instance
• Compare to K nearest neighbors
– Label according to majority of K
• What should K be?
– Often 3, can train as well
Text Classification
Matching Topics and Documents
• Two main perspectives:
– Pre-defined, fixed, finite topics:
• “Text Classification”
– Arbitrary topics, typically defined by statement
of information need (aka query)
• “Information Retrieval”
Vector Space Information Retrieval
• Task:
– Document collection
– Query specifies information need: free text
– Relevance judgments: 0/1 for all docs
• Word evidence: Bag of words
– No ordering information
Vector Space Model
Tv
Program
Computer
Two documents: computer program, tv program
Query: computer program : matches 1 st doc: exact: distance=2 vs 0
educational program: matches both equally: distance=1
Vector Space Model
• Represent documents and queries as
– Vectors of term-based features
• Features: tied to occurrence of terms in collection
– E.g.


d j  (t1, j , t2, j ,..., t N , j ); qk  (t1,k , t2,k ,..., t N ,k )
• Solution 1: Binary features: t=1 if present, 0
otherwise
– Similiarity: number of terms in common
• Dot product

N

sim (qk , d j )   ti ,k ti , j
i 1
Vector Space Model II
• Problem: Not all terms equally interesting
– E.g. the vs dog vs Levow


d j  (w1, j , w2, j ,..., wN , j ); qk  (w1,k , w2,k ,..., wN ,k )
• Solution: Replace binary term features with
weights
– Document collection: term-by-document matrix
– View as vector in multidimensional space
• Nearby vectors are related
– Normalize for vector length
Vector Similarity Computation
• Similarity = Dot product
N
 
 
sim (qk , d j )  qk  d j   wi ,k wi , j
i 1
• Normalization:
– Normalize weights in advance
– Normalize post-hoc
 
sim (qk , d j ) 

N
i 1
wi ,k wi , j
i1 wi2,k
N

N
2
w
i 1 i , j
Term Weighting
• “Aboutness”
– To what degree is this term what document is about?
– Within document measure
– Term frequency (tf): # occurrences of t in doc j
• “Specificity”
– How surprised are you to see this term?
– Collection frequency
– Inverse document frequency (idf):
idf i  log(
N
)
ni
wi , j  tfi , j idf i
Term Selection & Formation
• Selection:
– Some terms are truly useless
• Too frequent, no content
– E.g. the, a, and,…
– Stop words: ignore such terms altogether
• Creation:
– Too many surface forms for same concepts
• E.g. inflections of words: verb conjugations, plural
– Stem terms: treat all forms as same underlying
Efficient Implementations
• Classification cost:
– Find nearest neighbor: O(n)
• Compute distance between unknown and all
instances
• Compare distances
– Problematic for large data sets
• Alternative:
– Use binary search to reduce to O(log n)
Efficient Implementation: K-D
Trees
• Divide instances into sets based on features
– Binary branching: E.g. > value
– 2^d leaves with d split path = n
• d= O(log n)
– To split cases into sets,
• If there is one element in the set, stop
• Otherwise pick a feature to split on
– Find average position of two middle objects on that dimension
» Split remaining objects based on average position
» Recursively split subsets
K-D Trees: Classification
R > 0.825?
Yes
No
No
Poor
No
L > 17.5?
Yes
R > 0.6?
R > 0.75?
Yes
Good
No
Good
L>9?
No
R > 1.175 ?
Yes
Poor
No
Good
Yes
Yes
R > 1.025 ?
No
Yes
Good Poor
Good
Efficient Implementation:
Parallel Hardware
• Classification cost:
– # distance computations
• Const time if O(n) processors
– Cost of finding closest
• Compute pairwise minimum, successively
• O(log n) time
Nearest Neighbor: Issues
• Prediction can be expensive if many
features
• Affected by classification, feature noise
– One entry can change prediction
• Definition of distance metric
– How to combine different features
• Different types, ranges of values
• Sensitive to feature selection
Nearest Neighbor: Analysis
• Issue:
– What is a good distance metric?
– How should features be combined?
• Strategy:
– (Typically weighted) Euclidean distance
– Feature scaling: Normalization
• Good starting point:
– (Feature Feature_mean)/Feature_standard_deviation
– Rescales all values - Centered on 0 with std_dev 1
Nearest Neighbor: Analysis
• Issue:
– What features should we use?
• E.g. Credit rating: Many possible features
– Tax bracket, debt burden, retirement savings, etc..
– Nearest neighbor uses ALL
– Irrelevant feature(s) could mislead
• Fundamental problem with nearest
neighbor
Nearest Neighbor: Advantages
• Fast training:
– Just record feature vector - output value set
• Can model wide variety of functions
– Complex decision boundaries
– Weak inductive bias
• Very generally applicable
Summary
• Machine learning:
– Acquire function from input features to value
• Based on prior training instances
– Supervised vs Unsupervised learning
• Classification and Regression
– Inductive bias:
• Representation of function to learn
• Complexity, Generalization, & Validation