* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Document
Perceptual control theory wikipedia , lookup
Personal knowledge base wikipedia , lookup
Time series wikipedia , lookup
Machine learning wikipedia , lookup
Hierarchical temporal memory wikipedia , lookup
History of artificial intelligence wikipedia , lookup
Pattern recognition wikipedia , lookup
Expert system wikipedia , lookup
Knowledge representation and reasoning wikipedia , lookup
Catastrophic interference wikipedia , lookup
Neural modeling fields wikipedia , lookup
Type-2 fuzzy sets and systems wikipedia , lookup
Convolutional neural network wikipedia , lookup
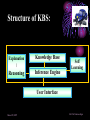
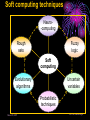
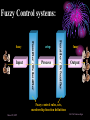
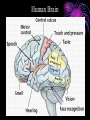
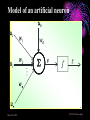
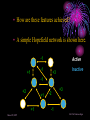
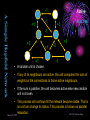
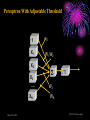
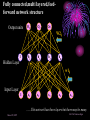
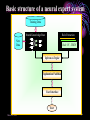
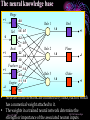
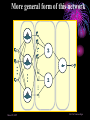
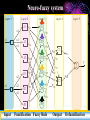
An Invited Lecture at AICTE-ISTE Sponsored Short Term Training Programme on Advances in Neuro-Fuzzy Systems and their Applications at A D Patel Institute of Technology, New Vidyanagar, Anand Neuro-Fuzzy Systems Part 1 Dr. Priti Srinivas Sajja P G Department of Computer Science and Technology Sardar Patel University Vallabh Vidyanagar-388 120 Introduction and Contact Information: • Name: Dr. Priti • Communication: Srinivas Sajja • Email : [email protected] • Mobile : 9824926020 • Website :priti.sajja.info • Academic qualifications : Ph. D in Computer Science • Thesis title: Knowledge-Based Systems for Socio-Economic Rural Development • Subject area of specialization : Artificial Intelligence • • Publications : 84 in International and National Books, Chapters and Papers Academic position : Associate Professor at Department of Computer Science Sardar Patel University Vallabh Vidyanagar 388120 March 20, 2007 Dr. Priti Srinivas Sajja Lecture Plan: Part 1: • AI and Soft Computing • Introduction to Fuzzy Logic • Introduction to Neural Network Part 2: • • • • • • Neuro fuzzy systems: fusion Advantages and requirements Approaches and structures Applications of neuro-fuzzy systems Tools and resources References March 20, 2007 Dr. Priti Srinivas Sajja Artificial Intelligence • “Artificial Intelligence(AI) is the study of how to make computers do things at which, at the moment, people are better” • -Elaine Rich, Artificial Intelligence, Mcgraw Hill Publications, 1986 March 20, 2007 Dr. Priti Srinivas Sajja Artificial Intelligence: AI involves • Studying the thought of humans process • Deals with representing those processes via machines. March 20, 2007 Dr. Priti Srinivas Sajja AI implementation leads to: • • • • Intelligence become permanent Speedy problem solving Ease of duplication Less expensive • Ease of documentation etc. March 20, 2007 Dr. Priti Srinivas Sajja Knowledge-Based Systems: K Knowledge-Based Systems (KBS) are Productive Artificial Intelligence Tools working in a narrow domain. March 20, 2007 Dr. Priti Srinivas Sajja How Knowledge is organized?: Volume Complexity & Sophistication Wisdom(experience) Knowledge(synthesis) Information(analysis) Data Data Pyramid Source: Tuthill & Leavy, modified March 20, 2007 Dr. Priti Srinivas Sajja Structure of KBS: Explanation / Knowledge Base Reasoning Inference Engine Self Learning User Interface March 20, 2007 Dr. Priti Srinivas Sajja Soft computing techniques Neuro-computing Rough sets Fuzzy logic Soft computing Evolutionary algorithms Uncertain variables Probabilistic techniques March 20, 2007 Dr. Priti Srinivas Sajja Fuzzy numbers and logic: Crisp 8 6 7 8 9 10 9 10 Fuzzy 8 6 March 20, 2007 7 8 Dr. Priti Srinivas Sajja Fuzzy Logic and Systems: • Humans routinely and subconsciously place things into classes whose meaning and significance are well understood but whose boundaries are not well defined. • Hot season, large car, young boy and rich people are the examples for the same. March 20, 2007 Dr. Priti Srinivas Sajja Membership functions: • Temperature is low Crisp Set: A set of temperature T which consists all temperature reading between 0* c to 40* c. 1 0.5 That is if t=27*c the tT 0 10 20 30 Low(t)=0.98 if t=10 *c March 20, 2007 40 But it is said that “the temperature is very low” then one can not exactly claim that low temp t is a member of T Dr. Priti Srinivas Sajja Another example….Set of tall people… Crisp set 1.0 Fuzzy set 1.0 .9 Membership .5 function 5’10’’ 5’10’’ 6’2’’ Heights Heights “tall” in Asia MFs .8 “tall” in the US .5 “tall” in xyz .1 5’10’’ March 20, 2007 Heights Dr. Priti Srinivas Sajja Air conditioning machine example: March 20, 2007 Dr. Priti Srinivas Sajja Fuzzy Control systems: crisp Process Fuzzifier / Defuzzifier Input Fuzzifier / Defuzzifier fuzzy fuzzy Output Fuzzy control rules, sets, membership function definitions March 20, 2007 Dr. Priti Srinivas Sajja Advantages of fuzzy logic: • Linguistic values used making it simpler to way human think. • Allows the solution to previously unsolved problems. • Rapid prototyping is possible as knowledge is not required before starting work. March 20, 2007 Dr. Priti Srinivas Sajja Advantages of fuzzy logic : • Cheaper to make than conventional system as easier to design • Increased robustness. • Simpler knowledge acquisition and representation. • A few rules are used to describe great complexity. March 20, 2007 Dr. Priti Srinivas Sajja Connectionist system: • Objective: Not to mimic brain functionality but to receive inspiration from the fact about how brain is working. • Characterized by: • A large number of very simple neuron like processing elements. • A large number of weighted connection between the elements. This weights encode the knowledge of a network. • Highly parallel, distributed control. • An emphasis on learning internal representation automatically. March 20, 2007 Dr. Priti Srinivas Sajja Human Brain March 20, 2007 Dr. Priti Srinivas Sajja Neuron March 20, 2007 Dr. Priti Srinivas Sajja Neuron March 20, 2007 Dr. Priti Srinivas Sajja Model of an artificial neuron March 20, 2007 Dr. Priti Srinivas Sajja Modeling Connectionist Systems(ANN): • Hopefiled network • Perceptron • Multi-layer feed forward back propogation March 20, 2007 Dr. Priti Srinivas Sajja • How are these features achieved? • A simple Hopefield network is shown here. -1 Active -1 +1 Inactive +3 -1 +2 +1 +1 March 20, 2007 -2 +3 -1 Dr. Priti Srinivas Sajja • In a Hopefield network, all processing units/elements are in two states either active or inactive. • Units are connected to each other with weighted, symmetric connections. • A positively weighted connection indicates that the units tend to active each other. • A negative connection allows an active unit to deactivate a neighbouring unit. March 20, 2007 Dr. Priti Srinivas Sajja -1 A Simple Hopfield Network Active -1 +1 Inactive +3 -1 +2 +1 +1 • A random unit is chosen. -2 +3 -1 • If any of its neighbours are active, the unit computes the sum of weights on the connections to those active neighbours. • If the sum is positive, the unit becomes active else new random unit is chosen. • This process will continue till the network become stable. That is no unit can change its status. This process is known as parallel relaxation. Dr. Priti Srinivas Sajja March 20, 2007 Perceptron With Adjustable Threshold 1 w0 X1 W1 W 2 X2 X3 …. XN March 20, 2007 ƒƒƒ W3 WN Dr. Priti Srinivas Sajja Perceptron With Many Inputs and Outputs March 20, 2007 ƒ ƒ ƒ 1 X1 X2 X3 …. XN …. …. ƒ Dr. Priti Srinivas Sajja • Consider the following figure: Decisio n Surface • This problem is linearly separatable • Given values of x1 and x2, we want to train a perceptron to output 1 if it thinks the input belongs to the class of white dots and 0 if it thinks the input belongs to the class of filled dots March 20, 2007 Dr. Priti Srinivas Sajja A Perception Learning to Solve a Classification Problem: K wo w1 w2 10 .41 -.17 .14 100 .22 -.14 .11 300 -.1 -.008 .07 635 -.49 -.1 March 20, 2007 .14 Dr. Priti Srinivas Sajja A Multi Layer Network- XOR Problem March 20, 2007 1 X1 -1.5 1.0 ƒ -9.0 1.0 X2 1 X1 -0.5 1.0 ƒ 1.0 X2 Dr. Priti Srinivas Sajja Fully connected,multi layered,feedforward network structure Output units O1 O2 Oc W2ij 1 h1 h2 h3 hB Hidden Layer w1ij Input Layer 1 x1 x2 x3 x4 xA ……This network has three layers but there may be many. March 20, 2007 Dr. Priti Srinivas Sajja Application of Neural Networks • Neural Networks may be divided into the following categories based on the complexity of the problem and the network’s behavior: • • Pattern recognizers and associative memories Pattern transformers • • • • • Connectionist Speech [3-layer backpropagation n/w] Connectionist Vision [Hopfield n/w-parallel relaxation] Combinatorial Problems Other Applications: compress images, to classify sonar signals, to drive a vehicle along a road Dynamic inferences • Still at a primitive stage March 20, 2007 Dr. Priti Srinivas Sajja Connectionist AI and Symbolic AI • Connectionist • Symbolic • Search – Parallel relaxation. • Search – State space traversal. • Knowledge Representation – very large number of realvalued connection Structures often stored as distributed patterns of activation. • Knowledge Representation – Predicate logic, semantic networks, frames, scripts. • Learning – Backpropagation, Boltzmann machines, reinforcement learning, unsupervised learning. • Learning – Macro-operators, version spaces, explanationbased learning, discovery. March 20, 2007 Dr. Priti Srinivas Sajja March 20, 2007 Dr. Priti Srinivas Sajja Neuro-Fuzzy Systems Part 2 NEURO-FUZZY Computing (for More Intelligent System) Combining Neural and Fuzzy: Neural Nets Knowledge Representation Trainability Fuzzy Logic Implicit, the system cannot be easy interpreted or modified (-) Explicit, verification and optimization easy and efficient (+++) Trains itself by learning from data sets (+++) None, you have to define everything explicitly (-) Get “best of both worlds”: Explicit Knowledge Representation from Fuzzy Logic with Training Algorithms from Neural Nets March 20, 2007 Dr. Priti Srinivas Sajja Combining Neural and Fuzzy • The key benefit of fuzzy logic is simple "if-then" relations to describe systems behaviour. • This leads to simpler time. solution in less design • However, the designer has to derive the "if-then" rules from the data sets manually, which requires a major effort with large data sets. • When data sets contain knowledge about the system to be designed, a neural net promises a solution as it can train itself from the data sets. March 20, 2007 Dr. Priti Srinivas Sajja • However, only few commercial applications of neural nets exist. This is a contrast to fuzzy logic, which is a very common design technique in Asia and Europe. • As neural net solutions remain a “black box” , it is impossible to interpret or manually change it • Selection of the appropriate net model and setting the parameters of the learning algorithm is still a "black art" and requires long experience. • Of the aforementioned reasons, the lack of an easy way to verify and optimize a neural net solution is probably the major limitation. March 20, 2007 Dr. Priti Srinivas Sajja • That is both neural nets and fuzzy logic are powerful design techniques that have its strengths and weaknesses. • Neural nets can learn from data sets while fuzzy logic solutions are easy to verify and optimize. • A clever combination of the two technologies delivers best of both worlds. March 20, 2007 Dr. Priti Srinivas Sajja Hybrid Systems Neuro-fuzzy Genetic neural Fuzzy genetic Probabilistic reasoning Fuzzy neuro Approximate reasoning genetic Case based reasoning Knowledge-based Systems Fuzzy logic Machine Intelligence Data Driven Systems Neural network system Evolutionary computing Non-linear Dynamics Rough sets Pattern recognition and learning Chaos theory Rescaled range analysis (wavelet) Fractal analysis Machine Intelligence: A core concept for grouping various advanced technologies with Learning Dr. Priti Srinivas Sajja March 20, 2007 Possible Integrations: Fuzzy Logic + ANN ANN + GA Fuzzy Logic + ANN + GA Fuzzy Logic + ANN + GA + Rough Set Neuro-fuzzy hybridization is the most visible integration realized so far. ANN: Artificial Neural Network GA: Genetic Algorithms March 20, 2007 Dr. Priti Srinivas Sajja Comparison of Expert Systems, Fuzzy Systems, Neural Networks and Genetic Algorithms ES Knowledge representation Uncertainty tolerance Imprecision tolerance Adaptability Learning ability Explanation ability Knowledge discovery and data mining Maintainability NN GA * The terms used for grading are: - bad, - rather bad, - rather good and March 20, 2007 FS - good Dr. Priti Srinivas Sajja Cooperative neuro-fuzzy approach: Reference: Neuro Fuzzy Systems: State-of-the-art Modeling Techniques Ajith Abraham School of Computing & Information Technology Monash University, Churchill 3842, Australia http://ajith.softcomputing.net Email: [email protected] March 20, 2007 Dr. Priti Srinivas Sajja Concurrent neuro-fuzzy approach: Reference: Neuro Fuzzy Systems: State-of-the-art Modeling Techniques Ajith Abraham School of Computing & Information Technology Monash University, Churchill 3842, Australia http://ajith.softcomputing.net Email: [email protected] March 20, 2007 Dr. Priti Srinivas Sajja Basic structure of a neural expert system Training Data Rule Extraction Neural Knowledge Base New Data Rule: IF - THEN Inference Engine Explanation Facilities User Interface User March 20, 2007 Dr. Priti Srinivas Sajja The neural knowledge base Wings +1 -0.8 Tail 0 Rule 1 Bird 1.0 -1.6 -0.7 +1 -0.2 Beak -1.1 -0.1 Rule 2 2.2 +1 Plane -1 1.0 0.0 -1.0 Feathers 2.8 +1 -1.6 -2.9 -1 Engine -1.1 1.9 Rule 3 Glider 1.0 -1 -1.3 • • Neurons in the network are connected by links, each of which has a numerical weight attached to it. The weights in a trained neural network determine the Dr. Priti Srinivas Sajja March 20, 2007 strength or importance of the associated neuron inputs. If we set each input of the input layer to either +1 (true), -1 (false), or 0 (unknown), we can give a semantic interpretation for the activation of any output neuron. For example, if the object has Wings (+1), Beak (+1) and Feathers (+1), but does not have Engine (-1), then we can conclude that this object is Bird (+1): X Rule 1 1 (-0.8) 0 (-0.2) 1 2.2 1 2.8 (-1) (-1.1) 5.3 0 YRule 1 YBird 1 March 20, 2007 Dr. Priti Srinivas Sajja We can similarly conclude that this object is not Plane: X Rule 2 1 (-0.7) 0 (-0.1) 1 0.0 1 (-1.6) (-1) 1.9 -4.2 0 YRule 2 YPlane -1 and not Glider: X Rule 3 1 (-0.6) 0 (-1.1) 1 (-1.0) 1 (-2.9) (-1) (-1.3) -4.2 0 YRule 3 YGlider -1 March 20, 2007 Dr. Priti Srinivas Sajja By attaching a corresponding question to each input neuron, we can enable the system to prompt the user for initial values of the input variables: Neuron: Wings Question: Does the object have wings? Neuron: Tail Question: Does the object have a tail? Neuron: Beak Question: Does the object have a beak? Neuron: Feathers Question: Does the object have feathers? Neuron: Engine Question: Does the object have an engine? March 20, 2007 Dr. Priti Srinivas Sajja An inference can be made if the known net weighted input to a neuron is greater than the sum of the absolute values of the weights of the unknown inputs. n n i 1 j 1 xi wi w j where i known, j known and n is the number of neuron inputs. March 20, 2007 Dr. Priti Srinivas Sajja An example of a multi-layer knowledge base Rule 1: IF a1 AND a3 THEN b1 (0.8) Rule 5: IF a5 THEN b3 (0.6) Rule 2: IF a1 AND a4 THEN b1 (0.2) Rule 6: IF b1 AND b3 THEN c1 (0.7) Rule 3: IF a2 AND a5 THEN b2 (-0.1) Rule 7: IF b2 THEN c1 (0.1) Rule 4: IF a3 AND a4 THEN b3 (0.9) Rule 8: IF b2 AND b3 THEN c2 (0.9) Input Layer a1 Conjunction Layer 1.0 R1 1.0 a2 1.0 R2 Disjunction Layer Conjunction Layer 0.8 0.2 b1 1.0 R6 1.0 a3 1.0 R3 -0.1 b2 1.0 a4 1.0 Disjunction Layer R4 0.9 R5 0.6 b3 1.0 1.0 1.0 1.0 0.7 0.1 c1 R7 0.9 c2 R8 1.0 a5 March 20, 2007 1.0 Dr. Priti Srinivas Sajja More general form of this network March 20, 2007 Dr. Priti Srinivas Sajja Neuro-fuzzy system Layer 1 Layer 2 x1 x1 x1 x1 Layer 3 A1 A1 R1 A2 A2 R2 Layer 4 R1 R2 wR3 A3 A3 B1 B1 R3 R3 R4 R4 x2 x2 x2 B2 B2 R5 R5 x2 B3 B3 Layer 5 C1 wR6 C1 wR1 wR2 wR4 y C2 C2 wR5 R6 R6 March 20, 2007 Input Fuzzification Fuzzy Rule Output Dr. Priti Srinivas Sajja Defuzzification Each layer in the neuro-fuzzy system is associated with a particular step in the fuzzy inference process. Layer 1 is the input layer. Each neuron in this layer transmits external crisp signals directly to the next layer. That is, yi(1) xi(1) Layer 2 is the fuzzification layer. Neurons in this layer represent fuzzy sets used in the antecedents of fuzzy rules. A fuzzification neuron receives a crisp input and determines the degree to which this input belongs to the neuron’s fuzzy set. March 20, 2007 Dr. Priti Srinivas Sajja The activation function of a membership neuron is set to the function that specifies the neuron’s fuzzy set. One may use triangular sets, and therefore, the activation functions for the neurons in Layer 2 are set to the triangular membership functions. A triangular membership function can be specified by two parameters {a, b} as follows: yi( 2) March 20, 2007 b ( 2) 0 , if x a i 2 2 xi( 2) - a b b ( 2) 1 , if a - xi a b 2 2 b ( 2) 0 , if x a i 2 Dr. Priti Srinivas Sajja Layer 3 is the fuzzy rule layer. Each neuron in this layer corresponds to a single fuzzy rule. A fuzzy rule neuron receives inputs from the fuzzification neurons that represent fuzzy sets in the rule antecedents. For instance, neuron R1, which corresponds to Rule 1, receives inputs from neurons A1 and B1. In a neuro-fuzzy system, intersection can be implemented by the product operator. Thus, the output of neuron i in Layer 3 is obtained as: yi(3) March 20, 2007 x1(i3) x2(3i ) xk(3i ) (3) yR 1 A1 B1 R1 Dr. Priti Srinivas Sajja Layer 4 is the output membership layer. Neurons in this layer represent fuzzy sets used in the consequent of fuzzy rules. An output membership neuron combines all its inputs by using the fuzzy operation union. This operation can be implemented by the probabilistic OR. That is, yi( 4) x1(i4) x2( 4i ) xli( 4) (4) yC1 R3 R6 C1 The value of C1 represents the integrated firing strength of fuzzy rule neurons R3 and R6. March 20, 2007 Dr. Priti Srinivas Sajja Layer 5 is the defuzzification layer. Each neuron in this layer represents a single output of the neuro-fuzzy system. It takes the output fuzzy sets clipped by the respective integrated firing strengths and combines them into a single fuzzy set. Neuro-fuzzy systems can apply standard defuzzification methods, including the centroid technique. We can use the sum-product composition method. March 20, 2007 Dr. Priti Srinivas Sajja The sum-product composition calculates the crisp output as the weighted average of the centroids of all output membership functions. For example, the weighted average of the centroids of the clipped fuzzy sets C1 and C2 is calculated as, C1 aC1 bC1 C 2 aC 2 bC 2 y C1 bC1 C 2 bC 2 March 20, 2007 Dr. Priti Srinivas Sajja Neuro-fuzzy systems: summary The combination of fuzzy logic and neural networks constitutes a powerful means for designing intelligent systems. Domain knowledge can be put into a neuro-fuzzy system by human experts in the form of linguistic variables and fuzzy rules. When a representative set of examples is available, a neuro-fuzzy system can automatically transform it into a robust set of fuzzy IF-THEN rules, and thereby reduce our dependence on expert knowledge when building intelligent systems. March 20, 2007 Dr. Priti Srinivas Sajja Applications and Examples…. March 20, 2007 Dr. Priti Srinivas Sajja Flexible neuro-fuzzy system L. Rutkowski and K. Cpałka „Flexible Neuro-Fuzzy Systems”, IEEE Trans. Neural Networks, vol. 14, pp. 554-574, May 2003 March 20, 2007 Dr. Priti Srinivas Sajja Knowledge-based ANN for learning and rule extraction • Combine the strengths of different AI techniques, e.g. ANN and rule-based systems or fuzzy logic • FuNN (Kasabov et al, 1997) • Learning from data and rule extraction, e.g.: R1: IF x1 is Small (DI11) and x2 is Small (DI21) THEN y is Small (CF1), R2: IF x1 is Large (DI12) and x2 is Large (DI22) THEN y is Large (CF2). March 20, 2007 Dr. Priti Srinivas Sajja Prototype rules extracted from DENFIS and EFuNN after model and data integration • Takagi-Sugeno fuzzy rules (DENFIS): • Rule 1: IF x1 is (-0.05, 0.05, 0.14) and x2 is (0.15,0.25,0.35) THEN y = 0.01 + 0.7x1 + 0.12x2 Rule 2: IF x1 is (0.02, 0.11, 0.21) and x2 is (0.45,0.55, 0.65) THEN y = 0.03+ 0.67x1+ 0.09 x2 Rule 3: IF x1 is (0.07, 0.17, 0.27) and x2 is (0.08,0.18,0.28) THEN y = 0.01 +0.71x1 + 0.11x2 Rule 4: IF x1is (0.26, 0.36, 0.46) and x2 is (0.44,0.53,0.63) THEN y = 0.03+ 0.68x1+ 0.07x2 Rule 5: IF x1is (0.35, 0.45, 0.55) and x2 is (0.08,0.18,0.28) THEN y = 0.02 + 0.73x1+ 0.06x2 Rule 6: IF x1is (0.52, 0.62, 0.72) and x2 is (0.45,0.55,0.65) THEN y = -0.21 + 0.95x1 + 0.28x2 Rule 7: IF x1is (0.60, 0.69,0.79) and x2 is (0.10,0.20,0.30) THEN y = 0.01+ 0.75x1+ 0.03x2 New rules: Rule 8: IF x1is (0.65,0.75,0.85) and x2 is (0.70,0.80,0.90) THEN y =-0.22+0.75x1+0.51x2 Rule 9: IF x1is (0.86,0.95,1.05) and x2 is (0.71,0.81,0.91) THEN • • • • • • • • • • • y =0.03 + 0.59x1+0.37x2 March 20, 2007 Zade-Mamdani fuzzy rules (ECF, EFuNN): Rule 1: IF x1 is (Low 0.8) and x2 is (Low 0.8) THEN y is (Low 0.8), radius R1=0.24; N1ex= 6 Rule 2: IF x1 is (Low 0.8) and x2 is (Medium 0.7) THEN y is (Small 0.7), R2=0.26, N2ex= 9 Rule 3: IF x1 is (Medium 0.7) and x2 is (Medium 0.6) THEN y is (Medium 0.6), R3 = 0.17,N3ex=17 Rule 4: IF x1 is (Medium 0.9) and x2 is (Medium 0.7) THEN y is (Medium 0.9), R4 = 0.08, N4ex=10 Rule 5: IF x1 is (Medium 0.8) and x2 is (Low 0.6) THEN y is (Medium 0.9), R5= 0.1, N5ex = 11 Rule 6: IF x1 is (Medium 0.5) and x2 is (Medium 0.7) THEN y is (Medium 0.7), R6= 0.07,N6ex= 5 New rules: Rule 7: IF x1 is (High 0.6) and x2 is (High 0.7) THEN y is (High 0.6), R7 = 0.2, N7ex = 12 Rule 8: IF x1 is (High 0.8) and x2 is (Medium 0.6) THEN y is (High 0.6), R8=0.1,N8ex= 5 Rule 9: IF x1 is (High 0.8) and x2 is (High 0.8) THEN y is (High3 0.8), R9= 0.1, N9ex = 6 Dr. Priti Srinivas Sajja NeuCom • Facilitates data analyses, data • • • • • • understanding, model creation and knowledge discovery Data management and data ontology Data analysis and feature extraction (statistical, PCA, clustering, SNR, …) Data modeling and rule extraction (classification, prediction, optimisation) Image recognition Module integration Free inspection copy from: www.theneucom.com or www.kedri.info/ March 20, 2007 Dr. Priti Srinivas Sajja Dynamic Evolving Neuro-Fuzzy System DENFIS for time series prediction , identification and control • Modeling, prediction and knowledge discovery from dynamic time series • Publication: Kasabov, N., and Song, Q., DENFIS: Dynamic Evolving Neural-Fuzzy Inference System and its Application for Time Series Prediction, IEEE Transactions on Fuzzy Systems, 2002, April March 20, 2007 Dr. Priti Srinivas Sajja A Neuro-Fuzzy Approach as Medical Diagnostic Interface R. Brause, F. Friedrich J.W.Goethe-University, Frankfurt a. M., Germany [email protected] March 20, 2007 Dr. Priti Srinivas Sajja A fuzzy agent to input vague parameters into multi-layer connectionist expert system: An application for stock market Priti Srinivas Sajja P1 fP2 P2 fP3 P3 fP4 fP5 Fuzzy Agent fP1 …… P4 ∑ P5 fP6 P6 fP7 P7 fP8 P8 Output ….. ….. ….. ….. ….. Parameters (fuzzy) Parameters (normalised) Input layer Hidden layer(s) Output layer Hybrid view of the proposed model March 20, 2007 Dr. Priti Srinivas Sajja March 20, 2007 Dr. Priti Srinivas Sajja