* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Moments
Scanning SQUID microscope wikipedia , lookup
Quantum electrodynamics wikipedia , lookup
Magnetic nanoparticles wikipedia , lookup
Eddy current wikipedia , lookup
Faraday paradox wikipedia , lookup
Electromagnetism wikipedia , lookup
Hall effect wikipedia , lookup
Magnetic monopole wikipedia , lookup
Superconductivity wikipedia , lookup
Magnetoreception wikipedia , lookup
Multiferroics wikipedia , lookup
Force between magnets wikipedia , lookup
Neutron magnetic moment wikipedia , lookup
Magnetohydrodynamics wikipedia , lookup
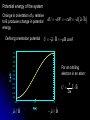
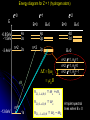
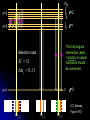
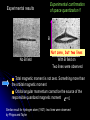
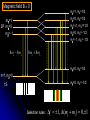
Restless electron(s) in an atom Hydrogen-like atoms: H, He+, Li2+ Multielectron atoms: many electrons are confined to a small space strong Coulomb ‘electron-electron’ interactions Magnetic properties (e.g., electrons interact with external magnetic fields) Electron spin Pauli exclusion principle The periodic table Orbital Magnetism and the Zeeman Effect An electron orbiting the nucleus of an atom should give rise to magnetic effects. Atoms are small magnets Magnetic field lines for a current loop Current I flowing in circle in x-y plane Magnetic dipole moment I A I Anˆ A current loop = A circulating charge q, q I T (T: period of motion) 2 r r2 A |L| | r p| r mq 2mq 2mq T T T q q Magnetic dipole I Anˆ Anˆ L T 2m q moment Orbital angular momentum Dipole moment vector is normal to orbit, with magnitude proportional to the angular momentum (e: positive) e L For electrons, q = e and 2m e I Magnetic dipole moment vector is anti-parallel to the angular momentum vector v Both L and are subject to space quantization ! Magnetic dipole moment in an external B field dL since B dt L̂ ˆ dLˆ ˆ and B Torque results in precession of the angular momentum vector Larmor precession frequency: eB L 2me dL Lsin d d L dt eL dt B sin dt B sin dt 2me Example: A spinning gyroscope(陀螺儀)in the gravity field the rate at which the axle rotates about the vertical axis d Mgh p dt I r mg Potential energy of the system Change in orientation of relative to B produces change in potential energy Defining orientation potential dU dW d d B U B B cos 1.0 0.8 0.6 0.4 For an orbiting electron in an atom: U (B) 0.2 0.0 -0.2 e U LB 2m -0.4 -0.6 -0.8 -1.0 0.0 // B 0.5 1.0 // B Quantum consideration for hydrogen-like atoms Magnetic dipole moment for the rotating electron magnitude e e L 1 2m e 2m e z-component e e z Lz m 2m e 2m e Bohr magneton: B e 2me 9.274 1024 J/T Quantization of L and Lz means that and z are also quantized !! (Note that electron has probability distribution, not classical orbit) U B Total energy: e e eB LB Lz B m 2me 2me 2me Lm ml 0, 1, 2, , l E ( B) En Lm En B Bm Degeneracy partially broken: total energy depends on n and m (magnetic quantum number) Energy diagram for Z = 1 (hydrogen atom) =0 =1 E B=0 4s 3s -0.85eV -1.5eV -3.4eV n=2 2s n=2 =2 B0 4d 3d 2p B0 -13.6eV 1s n=2, =1, m=1 n=2, =1, m=0 n=2, =1, m=1 B B 2,1,11,0,0 o L 2,1,01,0,0 o n=1 B0 4p 3p E L o B=0 2,1,11,0,0 o L A triplet spectral lines when B 0 Normal Zeeman Effect 1896 Lorentz Zeeman 1853~1928 1865~1943 First observation of spectral line splitting due to magnetic field Requires Quantum Mechanics (1926) to explain n=2, =1 o n=1, =0 B>0 B=0 o L 1902 1902 m=1 m=0 m=1 o L m=0 m 2 1 0 1 2 1 0 1 n=3 n=2 =1 The total angular momentum (atom + photon) in optical transitions should be conserved Selection rules: 1 m 0, 1 0 n=1 3, 2 =2 2,1 3,1 =0 (Cf. Serway, Figure 9.5) Normal Zeeman effect – A triplet of equally spaced spectral lines when B 0 is expected homogeneous B field Selection rule Energy spacing e L B B B = 5.810-5 [eV/T] B[T] 2me For B = 1 Tesla, L 5.79 105 eV, L 8.78 1010 rad/s Ex. Relative energy change in the Zeeman splitting. Consider the optical transitions from 2P to 1S states in an external magnetic field of 1 T E L B B E2 E1 E2 E1 E2 E1 5.8 105 a few tens eV Cf. Zeeman used Na atoms 106 Leiden (08/2008) Mysteries: Other splitting patterns such as four, six or even more unequally spaced spectral lines when B 0 are observed Anomalous Zeeman effect inhomogeneous magnetic field existence of electron spin (2/24/2009) Electron Spin Stern Gerlach Direct observation of energy level splitting in an inhomogeneous magnetic field F U r B Z B Let the magnitude of B field depend only on z: B(x,y,z) = B(z) F Fz zˆ z dB zˆ dz Translational force in z-direction is proportional to z-component of magnetic dipole moment z Quantum prediction: F z dB dB zˆ ms g B zˆ dz dz g ≈ 2 for electrons 1888~1969 1943 1889~1979 F U r B Z B B B B Z xˆ Z yˆ Z zˆ x y z ˆ ( x, y , z ) zB ˆ ( z) B zB Ag atom in ground state Electronic configuration of Ag atom: [Kr]4d105s1 outermost electron Bz = B(z) =0, m=0 Expectation from normal Zeeman effect: No splitting ? Stern and Gerlach (1922) Ex. expectations for = 1, three discrete lines Experimental confirmation of space quantization !! Experimental results B Not zero, but two lines No B field With B field on Two lines were observed Total magnetic moment is not zero. Something more than the orbital magnetic moment Orbital angular momentum cannot be the source of the responsible quantized magnetic moment = 0 Similar result for hydrogen atom (1927): two lines were observed by Phipps and Taylor Gerlach's postcard, dated 8 February 1922, to Niels Bohr. It shows a photograph of the beam splitting, with the message, in translation: “Attached [is] the experimental proof of directional quantization. We congratulate [you] on the confirmation of your theory.” 1925, Goudsmit and Uhlenbeck Goudsmit Uhlenbeck 1902~1978 1900~1988 proposed that electron carries intrinsic angular momentum called “spin” Experimental result requires 1 s 2 2s 1 2 s: spin quantum number a half integer !! New angular momentum operator S Sz ms 1 2 S s s 1 2 2 1 3 2 2 Both cannot be changed in any way 2 Intrinsic property Electron Spin The new kind of angular momentum is called the electron SPIN Why call it spin? If the electron were spinning on its axis, it would have angular momentum and a magnetic moment regardless of its spatial motion However, this “spinning” ball picture is not realistic, because it would require that the tiny electron be spinning so fast that parts would travel faster than c ! So we cannot picture the spin in any simple way … the electron’s spin is simply another degree-of-freedom available to electron A spin magnetic moment is associated with the spin angular momentum s S U s s B B=0 B0 sB sB E 2s|B| B s 9.2848 1024 J/T -- electron magnetic moment B = 9.2741 1024 J/T (the "Bohr magneton") Note: All particles possess spin (e.g., protons, neutrons, quarks, photons) Picturing a Spinning Electron We may picture electron spin as the result of spinning charge distribution Spin is a quantum property Electron is a point-like object with no internal coordinates Magnetic dipole moment e s g e S 2me ge: electron gyromagnetic ratio = 2.00232 from measurement (Agree with prediction from Quantum Electrodynamics) Only two allowed orientations of spin vector S So, we need FOUR quantum numbers to specify the electronic state of a hydrogen atom n, , m, ms (where ms = 1/2 and +1/2) Complete wavefunction: product of spatial wave function and spin wave function (r ) e + : spin-up wavefunction - : spin-down wavefunction Spin wave functions : eigenfunctions of [Sz] and [S2] Sz 1 2 3 S 2 4 Sz 1 2 3 S 4 2 2 2 it Wavefunction: e ( r ,) Rn r Ym , states Eigenvalues n = 1, 2, 3,…. En = 13.6(Z/n)2 eV = 0, 1, 2,…, n-1 L 1 Lz m Sz ms / 2 m = 0, 1, 2,…, ms = 1/2 Degeneracy in the absence of a magnetic field: Each state has 2(2+1) degenerate states Each state n has 2n2 degenerate states two spin orientations n 1 2 2 1 0 In strong magnetic fields, the torques are large Total magnetic moment: Both the L and S angular momenta precess independently around the B field L s eB e U ( L s ) B (ml g ems ) B Lz ge S z 2me 2me For an electron: ge = 2 spin up spin down ms = 1/2 e U m 1 B 2me ms = 1/2 U e m 1 B 2me B=0 For a given m, U U U 2 e B 2 L 2 B B 2me Contribution to energy shifts B0 sB sB (orientation of s) Magnetic field B 0 m=1, ms=1/2 m=0, ms=1/2 m=1 2P m=0 m=1 m=1, ms=1/2 m=0, ms=1/2 m=1, ms=1/2 o L o L m=0, ms=1/2 n=1,m=0 m=0, ms=1/2 1S Selection rules: 1, (m ms ) 0, 1 Otto Stern: “one of the finest experimental physicists of the 20th century” (Serway) Specific heat of solids, a theoretical work under Einstein “The method of molecular rays” – the properties of isolated atoms and molecules may be investigated with macroscopic tools Molecules move in a straight line (between collisions) The Maxwell speed distribution of atoms/molecules Space quantization – the Stern-Gerlach experiment the de Broglie wavelengths of helium atoms the magnetic moments of various atoms the very small magnetic moment of proton ! (The experimental value is 2.8 times larger than the theoretical value – still a mystery) electron spin Otto Stern – the Nobel Lecture, December 12, 1946 “The most distinctive characteristic property of the molecular ray method is its simplicity and directness. It enables us to make measurements on isolated neutral atoms or molecules with macroscopic tools. For this reason it is especially valuable for testing and demonstrating directly fundamental assumptions of the theory.” Stern –Gerlach experiment with ballistic electrons in solids Franck-Hertz Experiment Direct confirmation that the internal energy states of an atom are quantized (proof of the Bohr model of the atom) 4.9V As a tool for measuring the energy changes of the mercury atom Franck and Hertz used electrons, that means an atomic tool a Recent Breakthrough – Detection of a single electron spin! IBM scientists achieved a breakthrough in nanoscale magnetic resonance imaging (MRI) by directly detecting the faint magnetic signal from a single electron buried inside a solid sample Nature 430, 329 (2004) Next step – detection of single nuclear spin (660x smaller) Dutt et al., Science 316, 1312 (2007)
























![NAME: Quiz #5: Phys142 1. [4pts] Find the resulting current through](http://s1.studyres.com/store/data/006404813_1-90fcf53f79a7b619eafe061618bfacc1-150x150.png)










