* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Slide 1
Orchestrated objective reduction wikipedia , lookup
Chemical bond wikipedia , lookup
EPR paradox wikipedia , lookup
Canonical quantization wikipedia , lookup
Wave–particle duality wikipedia , lookup
Bell test experiments wikipedia , lookup
Atomic orbital wikipedia , lookup
Topological quantum field theory wikipedia , lookup
Coupled cluster wikipedia , lookup
Perturbation theory (quantum mechanics) wikipedia , lookup
Double-slit experiment wikipedia , lookup
Renormalization group wikipedia , lookup
Scalar field theory wikipedia , lookup
Yang–Mills theory wikipedia , lookup
Hydrogen atom wikipedia , lookup
Renormalization wikipedia , lookup
Quantum electrodynamics wikipedia , lookup
Perturbation theory wikipedia , lookup
Hidden variable theory wikipedia , lookup
History of quantum field theory wikipedia , lookup
Electron configuration wikipedia , lookup
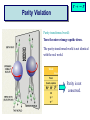
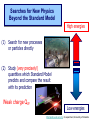
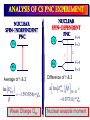
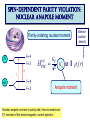
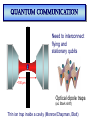
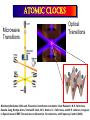
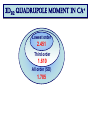
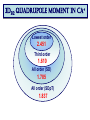
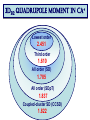
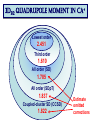
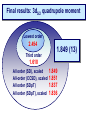
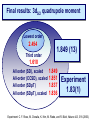
ICCMSE 2009 RHODES, GREECE October 30, 2009 Atomic Calculations for Future Technology and Study of Fundamental Problems Marianna Safronova Outline • Selected applications of atomic calculations • Study of fundamental symmetries: parity violation • Quantum information • Atomic clocks • Methods for high-precision atomic calculations • Overview • Computational challenges • Evaluation of the uncertainty • Development of the LCCSD + CI method • Future prospects study of Fundamental symmetries Parity violation studies with heavy atoms & search for Electron electric-dipole moment r ─r Parity Violation Parity-transformed world: Turn the mirror image upside down. The parity-transformed world is not identical with the real world. Parity is not conserved. Searches for New Physics Beyond the Standard Model High energies (1) Search for new processes or particles directly (2) Study (very precisely!) quantities which Standard Model predicts and compare the result with its prediction Weak charge QW Low energies http://public.web.cern.ch/, Cs experiment, University of Colorado The most precise measurement of PNC amplitude (in cesium) C.S. Wood et al. Science 275, 1759 (1997) F=4 7s F=3 2 1 6s F=4 F=3 Im EPNC 0.3% accuracy b 1.6349(80) mV cm 1.5576(77) mV cm Stark interference scheme to measure ratio of the PNC amplitude and the Stark-induced amplitude b 1 2 Parity violation Nuclear spin-independent PNC: Searches for new physics beyond the Standard Model e q e Z0 q Weak Charge QW Nuclear spin-dependent PNC: Study of PNC In the nucleus a Nuclear anapole moment Analysis of CS PNC experiment Nuclear spin-independent PNC 7s Nuclear spin-dependent PNC F=4 7s F=3 2 1 6s F=3 Difference of 1 & 2 Average of 1 & 2 Im E si PNC b 1.5935(56) F=4 6s mV Weak Charge QW cm sd Im EPNC b 3443 0.077(11) mV cm Nuclear anapole moment Spin-dependent parity violation: Nuclear anapole moment a Parity-violating nuclear moment F=4 7s F=3 2 H (a) PNC GF 2 a α I v ( r ) 1 6s F=4 F=3 Valence nucleon density Anapole moment Nuclear anapole moment is parity-odd, time-reversal-even E1 moment of the electromagnetic current operator. Constraints on nuclear weak coupling contants W. C. Haxton and C. E. Wieman, Ann. Rev. Nucl. Part. Sci. 51, 261 (2001) Nuclear anapole moment: test of hadronic weak interations The constraints obtained from the Cs experiment were found to be inconsistent with constraints from other nuclear PNC measurements, which favor a smaller value of the133Cs anapole moment. All-order (LCCSD) calculation of spin-dependent PNC amplitude: k = 0.107(16)* [ 1% theory accuracy ] No significant difference with previous value k = 0.112(16) is found. NEED NEW EXPERIMENTS!!! *M.S. Safronova, Rupsi Pal, Dansha Jiang, M.G. Kozlov, W.R. Johnson, and U.I. Safronova, Nuclear Physics A 827 (2009) 411c Quantum information Quantum communication, cryptography and quantum information processing Need calculations of atomic properties Optimizing the fast Rydberg quantum gate, M.S. Safronova, C. J. Williams, and C. W. Clark, Phys. Rev. A 67, 040303 (2003) . Magic wavelengths for the ns-np transitions in alkali-metal atoms, Bindiya Arora, M.S. Safronova, and C. W. Clark, Phys. Rev. A 76, 052509 (2007). Quantum Computer (Innsbruck) P1/2 D5/2 „quantum bit“ S1/2 Quantum communication Need to interconnect flying and stationary qubits ~100 µm Optical dipole traps (ac Stark shift) Thin ion trap inside a cavity (Monroe/Chapman, Blatt) problem Atom in state A sees potential UA Atom in state B sees potential UB What is magic wavelength? Atom in state A sees potential UA Atom in state B sees potential UB Magic wavelength magic is the wavelength for which the optical potential U experienced by an atom is independent on its state U ( ) Atomic polarizability Locating magic wavelength magic α S State P State wavelength Magic wavelengths for the ns-np transitions in alkali-metal atoms, Bindiya Arora, M.S. Safronova, and C. W. Clark, Phys. Rev. A 76, 052509 (2007). Atomic clocks Microwave Transitions Optical Transitions Blackbody Radiation Shifts and Theoretical Contributions to Atomic Clock Research, M. S. Safronova, Dansha Jiang, Bindiya Arora, Charles W. Clark, M. G. Kozlov, U. I. Safronova, and W. R. Johnson, to appear in Special Issue of IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control (2009). motiation: next generation Atomic clocks Next - generation ultra precise atomic clock http://CPEPweb.org Atoms trapped by laser light The ability to develop more precise optical frequency standards will open ways to improve global positioning system (GPS) measurements and tracking of deep-space probes, perform more accurate measurements of the physical constants and tests of fundamental physics such as searches for gravitational waves, etc. applications Parity Violation P1/2 Atomic Clocks NEED ATOMIC PROPERTIES D5/2 „quantum bit“ S1/2 Quantum information How to accurately calculate atomic properties? Very precise calculation of atomic properties We also need to evaluate uncertainties of theoretical values! Atomic Properties Magic wavelength BBR shifts Parity nonconserving van der Waals coefficients amplitudes Derived: Weak charge QW, Hyperfine Anapole moment constants Lifetimes Isotope shifts Line strengths Oscillator strengths ac and dc Polarizabilities Energies Quadrupole moments Transition probabilities and others ... Fine-structure intervals Electron electric-dipole moment enhancement factors Branching ratios BBR shifts Atom-wall interaction Wavelengths constants Theory: All-order method (relativistic linearized coupledcluster approach) Perturbation theory: Correlation correction to ground state energies of alkali-metal atoms Linearized coupledcluster method The linearized coupled-cluster method sums infinite sets of many-body perturbation theory terms. The wave function of the valence electron v is represented as an expansion that includes all possible single, double, and partial triple excitations. Cs: atom with single (valence) electron outside of a closed core. 1s22s22p63s23p63d104s24p64d105s25p66s core 1s2…5p6 6s valence electron All-order atomic wave function (SD) Lowest order Single-particle excitations Double-particle excitations Core core valence electron any excited orbital All-order atomic wave function (SD) Lowest order Core core valence electron any excited orbital v(0) Single-particle excitations ma ma am† aa v(0) † (0) a a mv m v v mv Double-particle excitations 1 2 mnab mnab am† an† ab aa v(0) mna mnva am† an† aa av v(0) Triples excitations, non-linear terms, extra perturbation theory terms, … Need for symbolic computing 1 2 (0) H S2 | v : ai aj al ak : am an ar as ad ac ab aa av :| 0c 2 800 terms! The code was developed to implement Wick’s theorem and simplify the resulting expressions. Symbolic program for coupled-cluster method & perturbation theory Input: expression of the type gijkl mnwa : ai a j al ak :: am an aa aw : in ASCII format. Output: simplified resulting formula in the LaTex format, ASCII output is also generated. Program features 1) The code is set to work with two or three normal products (all possible cases) with large number of operators. 2) The code differentiates between different types of indices, i.e. core (a,b,c,…), valence (v,w,x,y,...), excited orbitals (m,n,r,s,…), and general case (i, j, k, l,…). 3) The operators are ordered as required in the same order for all terms. gmnba rswc am an ar as aa ab ac aw 4) The expression is simplified to account for the identical terms and symmetry rules, gijkl g jilk . 5) The direct and exchange terms are joined together, gijkl gijkl gijlk . Symbolic computing for program generation The resulting expressions that need to be evaluated numerically contain very large number of terms, resulting in tedious coding and debugging. The symbolic program generator was developed for this purpose to automatically generate efficient numerical codes for coupled-cluster or perturbation theory terms. (1) abcd k1k2 k3 J k1 k2 k3 jc jd jw jw ' J k2 jc jw ' jd J jv ' k3 ja jw jb J jv k1 jc jb X k1 (cdab) X k2 (v ' w ' cd ) Z k3 (vwab) c d v ' w ' a b v ' w' jd ja Automated code generation Codes that write formulas Codes that write codes Input: Output: list of formulas to be programmed final code (need to be put into a main shell) Features: simple input, essentially just type in a formula! All-order method: Correlation correction to ground state energies of alkali-metal atoms Results for alkali-metal atoms: E1 matrix elements (a.u.) Na 3p1/2-3s K 4p1/2-4s Rb 5p1/2-5s Cs Fr 6p1/2-6s 7p1/2-7s All-order 3.531 4.098 4.221 4.478 4.256 Experiment 3.5246(23) 4.102(5) 4.231(3) 4.489(6) 4.277(8) Difference 0.18% 0.1% 0.24% 0.24% 0.5% Experiment Na,K,Rb: Theory U. Volz and H. Schmoranzer, Phys. Scr. T65, 48 (1996), Cs: R.J. Rafac et al., Phys. Rev. A 60, 3648 (1999), Fr: J.E. Simsarian et al., Phys. Rev. A 57, 2448 (1998) M.S. Safronova, W.R. Johnson, and A. Derevianko, Phys. Rev. A 60, 4476 (1999) Static polarizabilities of np states Theory [ 1 ] Experiment* Na 0 (3P1/2) 0 (3P3/2) 2 (3P3/2) K 0 (4P1/2) 0 (4P3/2) 2 (4P3/2) 606(6) 616(6) -109(2) 606.7(6) 614 (10) -107 (2) Rb 0 (5P1/2) 0 (5P3/2) 2 (5P3/2) 807(14) 869(14) -166(3) 810.6(6) 857 (10) -163(3) 359.9(4) 361.6(4) -88.4(10) Excellent agreement with experiments ! 359.2(6) 360.4(7) -88.3 (4) *Zhu et al. PRA 70 03733(2004) [1] Bindiya Arora, M.S. Safronova, and Charles W. Clark, Phys. Rev. A 76, 052509 (2007) Very brief summary of what we calculated with this approach Properties Systems • Energies • Transition matrix elements (E1, E2, E3, M1) Li, Na, Mg II, Al III, • Static and dynamic polarizabilities & applications Si IV, P V, S VI, K, Dipole (scalar and tensor) Ca II, In, In-like ions, Quadrupole, Octupole Ga, Ga-like ions, Rb, Light shifts Cs, Ba II, Tl, Fr, Th IV, Black-body radiation shifts U V, other Fr-like ions, Magic wavelengths Ra II • Hyperfine constants • C3 and C6 coefficients • Parity-nonconserving amplitudes (derived weak charge and anapole moment) • Isotope shifts (field shift and one-body part of specific mass shift) • Atomic quadrupole moments • Nuclear magnetic moment (Fr), from hyperfine data http://www.physics.udel.edu/~msafrono how to evaluate uncertainty of theoretical calculations? Theory: evaluation of the uncertainty HOW TO ESTIMATE WHAT YOU DO NOT KNOW? I. Ab initio calculations in different approximations: (a) Evaluation of the size of the correlation corrections (b) Importance of the high-order contributions (c) Distribution of the correlation correction II. Semi-empirical scaling: estimate missing terms Example: quadrupole moment of 3d5/2 state in Ca+ Electric quadrupole moments of metastable states of Ca+, Sr+, and Ba+, Dansha Jiang and Bindiya Arora and M. S. Safronova, Phys. Rev. A 78, 022514 (2008) 3D5/2 quadrupole moment in Ca+ Lowest order 2.451 3D5/2 quadrupole moment in Ca+ Lowest order 2.451 Third order 1.610 3D5/2 quadrupole moment in Ca+ Lowest order 2.451 Third order 1.610 All order (SD) 1.785 3D5/2 quadrupole moment in Ca+ Lowest order 2.451 Third order 1.610 All order (SD) 1.785 All order (SDpT) 1.837 3D5/2 quadrupole moment in Ca+ Lowest order 2.451 Third order 1.610 All order (SD) 1.785 All order (SDpT) 1.837 Coupled-cluster SD (CCSD) 1.822 3D5/2 quadrupole moment in Ca+ Lowest order 2.451 Third order 1.610 All order (SD) 1.785 All order (SDpT) 1.837 Coupled-cluster SD (CCSD) 1.822 Estimate omitted corrections Final results: 3d5/2 quadrupole moment Lowest order 2.454 Third order 1.849 (13) 1.610 All order (SD), scaled All-order (CCSD), scaled All order (SDpT) All order (SDpT), scaled 1.849 1.851 1.837 1.836 Final results: 3d5/2 quadrupole moment Lowest order 2.454 Third order 1.849 (13) 1.610 All order (SD), scaled All-order (CCSD), scaled All order (SDpT) All order (SDpT), scaled 1.849 1.851 1.837 1.836 Experiment 1.83(1) Experiment: C. F. Roos, M. Chwalla, K. Kim, M. Riebe, and R. Blatt, Nature 443, 316 (2006). More complicated systems relativistic All-order method Singly-ionized ions Summary of theory methods for PNC studies • Configuration interaction (CI) • Many-body perturbation theory • Relativistic all-order method (coupled-cluster) • Perturbation theory in the screened Coulomb interaction (PTSCI), all-order approach • Configuration interaction + second-order MBPT • Configuration interaction + all-order method* *under development Configuration interaction method ci i H Single-electron valence basis states i eff E 0 1 r1 r2 Example: two particle system: H eff h1 (r1 ) h1 (r2 ) h2 (r1 , r2 ) onebody part twobody part Configuration interaction + many-body perturbation theory CI works for systems with many valence electrons but can not accurately account for core-valence and core-core correlations. MBPT can not accurately describe valence-valence correlation for large systems but accounts well for core-core and core-valence correlations. Therefore, two methods are combined to acquire benefits from both approaches. Configuration interaction method + MBPT Heff is modified using perturbation theory expressions h1 h1 1 h2 h2 2 1 , 2 H eff E 0 are obtained using perturbation theory Problem: (1) Accuracy deteriorates for heavier systems owing to larger correlation corrections. (2) Accuracy will not be ultimately sufficient. Configuration interaction + all-order method Heff is modified using all-order excitation coefficients ~ 1 mn n m mn L L ~ ~ 2 mnkl k l m n mnkl Advantages: most complete treatment of the correlations and applicable for many-valence electron systems CI + ALL-ORDER RESULTS Two-electron binding energies, differences with experiment Atom Mg Ca Cd Sr Zn Ba Hg CI 1.9% 4.1% 9.6% 5.2% 8.0% 6.4% 11.8% 2.4% CI + MBPT CI + All-order 0.12% 0.6% 1.0% 0.9% 0.9% 1.7% 0.03% 0.3% 0.02% 0.3% 0.4 % 0.5% 0.5% Development of a configuration-interaction plus all-order method for atomic calculations, M.S. Safronova, M. G. Kozlov, W.R. Johnson, Dansha Jiang, Phys. Rev. A 80, 012516 (2009). CI + ALL-ORDER: Mg energies Experiment CI Dif(%) CI+MBPT Dif(%) CI+allorder Dif(%) 3s2 1S 0 182938 179536 1.9 182718 0.12 182880 0.03 3s4s 3S 1 41197 40399 1.9 41121 0.19 41162 0.08 3s4s 1S 0 43503 42662 1.9 43435 0.16 43478 0.06 3s3d 1D 2 46403 45117 2.8 46319 0.18 46373 0.06 3s3d 3D 1 47957 46967 2.1 47892 0.13 47944 0.03 3s3d 3D 2 47957 46967 2.1 47892 0.13 47941 0.03 3s3d 3D 3 47957 46967 2.1 47893 0.13 47936 0.04 3s3p 3P 0 21850 20905 4.3 21782 0.31 21837 0.06 3s3p 3P 1 21870 20926 4.3 21804 0.30 21856 0.06 3s3p 3P 2 21911 20966 4.3 21847 0.29 21901 0.04 3s3p 1P 1 35051 34488 1.6 35053 0.00 35068 -0.05 3s4p 3P 0 47841 46914 1.9 47766 0.16 47813 0.06 3s4p 3P 1 47844 46917 1.9 47769 0.16 47816 0.06 3s4p 3P 2 47851 46924 1.9 47776 0.16 47823 0.06 3s4p 1P 1 49347 48487 1.7 49290 0.12 49329 0.04 Cd energies, differences with experiment Expt. State J DIF(%) DIF(%) DIF(%) CI CI+MBPT CI+All-order 5s2 1S 0 208915 10 -1.0 0.02 5s5p 3P° 0 30114 19 -3.2 -0.53 1 30656 19 -3.1 -0.40 2 31827 19 -3.1 -0.46 5s5p 1P° 1 43692 11 -1.0 -0.09 5s6s 3S 1 51484 14 -1.6 -0.49 5s6s 1S 0 53310 13 -1.4 -0.35 5s5d 1D 2 59220 14 -1.5 -0.24 5s5d 3D 1 59486 14 -1.4 -0.22 2 59498 14 -1.4 -0.22 3 59516 14 -1.4 -0.22 Cd, Zn, and Sr Polarizabilities, preliminary results (a.u.) Zn CI CI+MBPT CI+All-order 4s2 1S0 44.13 37.22 37.02 4s4p 3P0 75.94 66.20 64.97 CI CI+MBPT CI+All-order 5s2 1S0 52.66 41.50 42.11 5s5p 3P0 86.94 70.72 70.72 CI+ All-order Recomm.* 197.4 197.2 Cd Sr 5s2 1S0 *From expt. matrix elements, S. G. Porsev and A. Derevianko, PRA 74, 020502R (2006). Conclusion Parity Violation Atomic Clocks P1/2 Future: New Systems New Methods, New Problems D5/2 „quantum bit“ S1/2 Quantum information Graduate students: Rupsi Pal Dansha Jiang Bindiya Arora Jenny Tchoukova Other collaborations: Michael Kozlov (PNPI, Russia) (Visiting research scholar at the University of Delaware) Walter Johnson (University of Notre Dame), Charles Clark (NIST) Ulyana Safronova (University of Nevada-Reno)