Download Power Point file

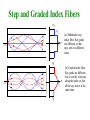
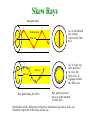
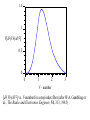
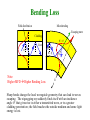
The Optical Fiber and
Light Wave Propagation
Xavier Fernando
Ryerson Comm. Lab
The Optical Fiber
• Fiber optic cable functions as a ”light guide,”
guiding the light from one end to the other
end.
• Fiber categories based on propagation:
– Single Mode Fiber (SMF)
– Multimode Fiber (MMF)
• Categories based on refractive index profile
– Step Index Fiber (SIF)
– Graded Index Fiber (GIF)
Step
Index
Fiber
n1
n2
n1>n2
• Uniform ref. index of n1 (1.44 < n1 < 1.46) within
the core and a lower ref. index n2 in the cladding.
• The core and cladding radii are a and b. Typically
2a/2b are 8/125, 50/125, 62.5/125, 85/125, or
100/140 µm.
• SIF is generally made by doping high-purity fused
silica glass (SiO2) with different concentrations of
materials like titanium, germanium, or boron.
Different Light Wave Theories
• Different theories explain light behaviour
• We will first use ray theory to understand
light propagation in multimode fibres
• Then use electromagnetic wave theory to
understand propagation in single mode
fibres
• Quantum theory is useful to learn photo
detection and emission phenomena
Refraction and Reflection
When Φ2 = 90,
Φ1 = Φc is the
Critical Angle
Snell’s Law: n1 Sin Φ1 = n2 Sin Φ2
Φc=Sin-1(n2/n1 )
Step Index Multimode Fiber
Fractional
n12  n22
n2
 1
refractive-index  
2
2n1
n1
profile
Ray description of different fibers
Single Mode Step Index Fiber
r
Buffer tube: d = 1mm
Protective polymerinc coating
Cladding: d = 125 - 150 m
n
Core: d = 8 - 10 m
n1
n2
The
of a typical
single-mode
withwavelength.
a tight buffer
Onlycross
one section
propagation
mode is
allowed infiber
a given
tube.
= diameter)
This (d
is achieved
by very small core diameter (8-10 µm)
SMF
offers
bit rate,
most
©
1999 S.O.
Kasap,highest
Optoelectronics
(Prentice
Hall)
widely used in telecom
Step Index Multimode Fiber
• Guided light propagation can be explained by
ray optics
• When the incident angle is smaller the
acceptance angle, light will propagate via TIR
• Large number of modes possible
• Each mode travels at a different velocity
Modal Dispersion
• Used in short links, mostly with LED sources
Graded Index Multimode Fiber
• Core refractive index gradually changes
towards the cladding
• The light ray gradually bends and the TIR
happens at different points
• The rays that travel longer distance also
travel faster
• Offer less modal dispersion compared to
Step Index MMF
Refractive Index Profile of
Step and Graded Index Fibers
n1
n2
a
n=
Graded
Step
n1
b
n2
a
n=
b
Step and Graded Index Fibers
n2
n1
3
2
1
O
n
(a) Multimode step
index fiber. Ray paths
are different so that
rays arrive at different
times.
n2
O
O'
O''
3
2
1
2
3
n1
n2
© 1999 S.O. Kasap, Optoelectronics (Prentice Hall)
n
(b) Graded index fiber.
Ray paths are different
but so are the velocities
along the paths so that
all the rays arrive at the
same time.
Total Internal Reflection
in Graded Index Fiber
(a)
TIR
n decreases step by step from one layer
to next upper layer; very thin layers.
(b)
TIR
Continuous decrease in n gives a ray
path changing continuously.
(a) A ray in thinly stratifed medium becomes refracted as it passes from one
layer to the next upper layer with lower n and eventually its angle satisfies TIR.
(b) In a medium where n decreases continuously the path of the ray bends
continuously.
© 1999 S.O. Kasap, Optoelectronics (Prentice Hall)
O
Total Internal Reflection
in Graded Index Fiber - II
nc
B'
B
2 B
1
B'
c/nb
c/na
B'
Ray 2
A
B''
nb
na
A
Ray 1
M
© 1999 S.O. Kasap, Optoelectronics (Prentice Hall)
We can visualize a graded index
fiber by imagining a stratified
medium with the layers of refractive
b indices na > nb > nc ... Consider two
close rays 1 and 2 launched from O
at the same time but with slightly
a different launching angles. Ray 1
just suffers total internal reflection.
O'
Ray 2 becomes refracted at B and
reflected at B'.
c
Skew Rays
Along the fiber
1
1, 3
3
(a) A meridional
ray always
crosses the fiber
axis.
Meridional ray
Fiber axis
2
2
1
2
1
Skew ray
Fiber axis
5
3
5
4
Ray path along the fiber
4
2
3
(b) A skew ray
does not have
to cross the
fiber axis. It
zigzags around
the fiber axis.
Ray path projected
on to a plane normal
to fiber axis
Illustration of the difference between a meridional ray and a skew ray.
Numbers represent reflections of the ray.
© 1999 S.O. Kasap, Optoelectronics (Prentice Hall)
Maxwell’s Equations
In a linear isotropic dielectric material with no currents and free of charges,
……..(1) (Faraday’s Law)
E: Electric Field
……….(2) (Maxwell’s Faraday equation)
H: Magnetic Field
……….(3) (Gauss Law)
……….(4) (Gauss Law for magnetism)
Taking the curl of (1) and using
and
…….(5)
The parameter ε is permittivity and μ is permeability.
Maxwell’s Equations
But from the vector identity
……(6)
Using (5) and (3),
Note v p 
1

…….(7)
Similarly taking the curl of (2), it can be shown
………(8)
(7) and (8) are standard wave equations. Note the Laplacian operation is,
1   E  1  2 E  2 E
 E
 2
r
 2
2
r r  r  r 
z
2
Maxwell’s Equation
• Electrical and magnetic vectors in cylindrical
coordinates are give by,
.…..(9)
……(10)
• Substituting (9) and (10) in Maxwell’s curl equations
….(11)
….(12)
….(13)
Maxwell’s Equation
• Also
----------(14)
----------(15)
----------(16)
• By eliminating variables, above can be rewritten such
that when Ez and Hz are known, the remaining
transverse components Er , Eφ, Hr , Hφ, can be
determined from (17) to (20).
Maxwell’s Equation
…………..(17)
…………..(18)
…..........(19)
.………… (20)
Substituting (19) and (20) into (16) results in
….…(21)
…….(22)
Electric and Magnetic Modes
Note (21) and (22) each contain either Ez or Hz only. This may
imply Ez and Hz are uncoupled. However. Coupling between
Ez and Hz is required by the boundary conditions.
If boundary conditions do not lead to coupling between field
components, mode solution will imply either Ez =0 or Hz =0.
This is what happens in metallic waveguides.
When Ez =0, modes are called transverse electric or TE modes
When Hz =0, modes are called transverse magnetic or TM modes
However, in optical fiber hybrid modes also will exist (both Ez
and Hz are nonzero). These modes are designated as HE or EH
modes, depending on either H or E component is larger.
Wave Equations for Step Index Fibers
• Using separation of variables
………..(23)
• The time and z-dependent factors are given by
………..(24)
• Circular symmetry requires, each field component must not
change when Ø is increased by 2п. Thus
…………(25)
• Where υ is an integer.
• Therefore, (21) becomes
….(26)
Wave Equations for Step Index Fibers
• Solving (26). For the fiber core region, the solution must
remain finite as r0, whereas in cladding, the solution
must decay to zero as r∞
• Hence, the solutions are
– In the core, (r < a),
Where, Jv is the Bessel function of first kind of order v
– In the cladding, (r > a),
Where, Kv is the modified Bessel functions of second kind
Bessel Functions First Kind
Modified Bessel first kind
Bessel Functions Second kind
Modified Bessel Second kind
Propagation Constant β
• From definition of modified Bessel function
• Since Kv(wr) must go to zero as r∞, w>0. This
implies that
• A second condition can be deduced from behavior of
Jv(ur). Inside core u is real for F1 to be real, thus,
• Hence, permissible range of β for bound solutions is
Meaning of u and w
Inside the core, we can write,
Outside the core, we can write,
q 2  u 2  k12   2
w2   2  k22
• Both u and w describes guided wave variation in
radial direction
– u is known as guided wave radial direction phase
constant (Jn resembles sine function)
– w is known as guided wave radial direction decay
constant (recall Kn resemble exponential function)
V-Number (Normalized Frequency)
Define the V-Number (Normalized Frequency) as,
 2a  2
2
V 2  (u 2  w2 )a 2  k12  k 22 a 2  
 n1  n2
  


2

Define the normalized propagation const b as,
w2 a 2 (  / k ) 2  n22 
b 2 
n12  n22 
V
All but HE11 mode will cut off when b = 0.
Hence, for single mode condition,
V
2a( NA)

 Vc  2.405

b
1
LP 01
0.8
LP 11
0.6
LP 21
0.4
LP 02
0.2
0
V
0
1
2
3
2.405
4
5
6
Normalized propagation constant b vs. V-number
for a step index fiber for various LP modes.
© 1999 S.O. Kasap, Optoelectronics (Prentice Hall)
1.5
1
V[d2(Vb)/dV2]
0.5
0
0
1
2
3
V - number
[d2(Vb)/dV2] vs. V-number for a step index fiber (after W.A. Gambling et
al., The Radio and Electronics Engineer, 51, 313, 1981)
© 1999 S.O. Kasap, Optoelectronics (Prentice Hall)
Field Distribution in the SMF
Fie ld of evanescent wave
(exponential decay)
y
n2
Field of guided wave
E(y,z,t) = E(y)cos(t – 0z)
E(y)
Light
m=0
n1
n2
The electric field pattern of the lowest mode traveling wave along the
guide. This mode has m = 0 and the lowest . It is often referred to as the
glazing incidence ray. It has the highest phase velocity along the guide.
© 1999 S.O. Kasap, Optoelectronics (Prentice Hall)
Mode-field
Diameter (2W0)
In a Single Mode Fiber,
E (r )  E0 exp( r 2 / w02 )
At r = wo,
E(Wo)=Eo/e
Typically Wo > a
Cladding Power Vs
Normalized Frequency
Modes
Vc = 2.4
Power in the cladding
Lower order modes have higher power in the cladding  larger MFD
Higher the Wavelength 
More the
Evanescent
Field
y
y
Cladding
2 > 1
1 > c
v g1
1 < cut-off
E(y)
Core
v g2 > v g1
2 < 1
Cladding
The electric field of TE 0 mode extends more into the
cladding as the wavelength increases. As more of the field
is carried by the cladding, the group velocity increases.
© 1999 S.O. Kasap, Optoelectronics (Prentice Hall)
Light Intensity
(a) The electric field
of the fundamental
mode
(b) The intensity in
the fundamental
mode LP01
(c) The intensity (d) The intensity
in LP 11
in LP 21
Core
E
Cladding
E01
r
The electric field distribution of the fundamental mode
in the transverse plane to the fiber axis z. The light
intensity is greatest at the center of the fiber. Intensity
patterns in LP 01, LP11 and LP21 modes.
© 1999 S.O. Kasap, Optoelectronics (Prentice Hall)
Fiber Key Parameters
Fiber Key Parameters
Effects of Dispersion and Attenuation
Dispersion for Digital Signals
Fiber
Digital signal
Information
Emitter
t
Photodetector
Information
Input
Output
Input Intensity
Output Intensity
² 
Very short
light pulses
0
T
t
t
0
~2² 
An optical fiber link for transmitting digital information and the effect of
dispersion in the fiber on the output pulses.
© 1999 S.O. Kasap, Optoelectronics (Prentice Hall)
Modal Dispersion
High order mode
Light pulse
Low order mode
Broadened
light pulse
Cladding
Core
Intensity
Intensity
Axial
0
Spread, 
t
Schematic illustration of light propagation in a slab dielectric waveguide. Light pulse
entering the waveguide breaks up into various modes which then propagate at different
group velocities down the guide. At the end of the guide, the modes combine to
constitute the output light pulse which is broader than the input light pulse.
© 1999 S.O. Kasap,Optoelectronics (Prentice Hall)
t
Major Dispersions in Fiber
• Modal Dispersion: Different modes travel at
different velocities, exist only in multimode
fibers
• This was the major problem in first generation
systems
• Modal dispersion was alleviated with single
mode fiber
– Still the problem was not fully solved
Dispersion in SMF
• Material Dispersion: Since n is a function of
wavelength, different wavelengths travel at
slightly different velocities. This exists in
both multimode and single mode fibers.
• Waveguide Dispersion: Signal in the
cladding travels with a different velocity
than the signal in the core. This phenomenon
is significant in single mode conditions.
Group Velocity (Chromatic) Dispersion
= Material Disp. + Waveguide Disp.
Cladding
Input
v g ( 1 )
Emitter
Very short
light pulse
v g ( 2 )
Intensity
Intensity
Core
Output
Intensity
Spectrum, ² 
Spread, ² 
1
o
2

0
t

All excitation sources are inherently non-monochromatic and emit within a
spectrum, ² , of wavelengths. Waves in the guide with different free space
wavelengths travel at different group velocities due to the wavelength dependence
of n1. The waves arrive at the end of the fiber at different times and hence result in
a broadened output pulse.
© 1999 S.O. Kasap, Optoelectronics (Prentice Hall)
Group Velocity Dispersion
t
Modifying Chromatic Dispersion
GVD = Material Disp. + Waveguide dispersion
• Material dispersion depends on the material
properties and difficult to alter
• Waveguide dispersion depends on fiber
dimensions and refractive index profile.
These can be altered to get:
– 1300 nm optimized fiber
– Dispersion Shifted Fiber (DSF)
– Dispersion Flattened Fiber (DFF)
Material and Waveguide Dispersions
Dispersion coefficient (ps km -1 nm -1 )
30
Dm
20
10
Dm + Dw
0
0
-10
Dw
-20
-30
1.1
1.2
1.3
1.4
 (m)
1.5
1.6
Material dispersion coefficient (Dm) for the core material (taken as
SiO2 ), waveguide dispersion coefficient (Dw ) (a = 4.2 m) and the
total or chromatic dispersion coefficient Dch (= Dm + Dw ) as a
function of free space wavelength,  
Dispersion coefficient (ps km-1 nm-1)
20
Dm
10
SiO2-13.5%GeO2
0
a (m)
Dw
4.0
3.5
3.0
–10
2.5
–20
1.2
1.3
1.4
1.5
1.6
 (m)
Material and waveguide dispersion coefficients in an
optical fiber with a core SiO 2-13.5%GeO2 for a = 2.5
to 4 m.
Different WG Dispersion Profiles
WGD is changed by
adjusting fiber profile
Dispersion Shifting/Flattening
(Standard)
(Low Dispersion throughout)
(Zero Disp. At 1550 nm)
Dispe rsion coefficient (ps km
-1
nm -1)
n
30
20
r
Dm
10
0
2
1
Dch = Dm + Dw
-10
Dw
-20
Thin laye r of c ladding
with a de pressed index
-30
1.1
1.2
1.3
1.4
(m)
1.5
1.6
1.7
Dispersion flattened fiber example. The material dispersion coefficient ( Dm) for the
core material and waveguide dispersion coefficient ( Dw) for the doubly clad fiber
result in a flattened small chromatic dispersion between 1 and 2.
Specialty Fibers with Different Index Profiles
1300 nm optimized
Dispersion Shifted
Specialty Fibers with Different Index Profiles
Dispersion
Flattened
Large area dispersion shifted
Large area dispersion flattened
Polarization Mode Dispersion
• Since optical fiber has a single axis of
anisotropy, differently polarized light travels at
slightly different velocity
• This results in Polarization Mode Dispersion
• PMD is usually small, compared to GVD or
Modal dispersion
• May become significant if all other dispersion
mechanisms are small
X and Y Polarizations
A Linear Polarized wave will always have two
orthogonal components.
These can be called x and y polarization components
Each component can be individually handled if
polarization sensitive components are used
Polarization Mode Dispersion (PMD)
Each polarization state
has a different
velocity  PMD
Birefringence
• Birefringence is the decomposition of a ray of light
into two rays types of (anisotropic) material
• In optical fibers, birefringence can be understood
by assigning two different refractive indices nx and
ny to the material for different polarizations.
• In optical fiber, birefringence happens due to the
asymmetry in the fiber core and due to external
stresses
• There are Hi-Bi, Low-Bi and polarization
maintaining fibers.
Total Dispersion
For Multi Mode Fibers:
(Note for MMF ΔTGVD ~= ΔTmat
For Single Mode Fibers:
But Group Velocity Disp.
Hence,
(ΔTpol is usually negligible )
Permissible Bit Rate
• As a rule of thumb the permissible total
dispersion can be up to 70% of the bit
period. Therefore,
0.7
• For full width pulses (Non Return to Zero bits) : B 
TTotal
0.35
• For half width pulses (Return to Zero bits) : B 
TTotal
Disp. & Attenuation Summary
Electrical signal (photocurrent)
1
0.707
Fiber
Sinusoidal signal
Photodetector
Emitter
t
Optical
Input
f = Modulation frequency
Pi = Input light power
Optical
Output
Po = Output light power
1 kHz
1 MHz
1 GHz
1 MHz
1 GHz
f
fel
Sinusoidal electrical signal
Po / Pi
0.1
0.05
0
t
0
t
1 kHz
fop
f
An optical fiber link for transmitting analog signals and the effect of dispersion in the
fiber on the bandwidth, fop.
© 1999 S.O. Kasap, Optoelectronics (Prentice Hall)
Fiber Optic Link is a Low Pass Filter for
Analog Signals
Attenuation Vs Frequency
Fiber attenuation does not depend on modulation frequency
Attenuation in Fiber
Attenuation Coefficient
P(0)dB  P( z )dB

dB/km
z
• Silica has lowest attenuation at 1550 nm
• Water molecules resonate and give high
attenuation around 1400 nm in standard fibers
• Attenuation happens because:
– Absorption (extrinsic and intrinsic)
– Scattering losses (Rayleigh, Raman and Brillouin…)
– Bending losses (macro and micro bending)
All Wave Fiber for DWDM
Lowest attenuation occurs at
1550 nm for Silica
Attenuation
characteristics
Bending Loss
Field distribution
Microbending
Escaping wave
Cladding

Core
 
Note:
Higher MFD  Higher Bending Loss

c

R
Sharp bends change the local waveguide geometry that can lead to waves
escaping. The zigzagging ray suddenly finds itself with an incidence
angle  that gives rise to either a transmitted wave, or to a greater
cladding penetration; the field reaches the outside medium and some light
energy is lost.
Micro-bending losses
Fiber
Production
The Fiber Cable