Download bagging

Bagging
LING 572
Fei Xia
1/24/06
Ensemble methods
• So far, we have covered several learning
methods: FSA, HMM, DT, DL, TBL.
• Question: how to improve results?
• One solution: generating and combining multiple
predictors
– Bagging: bootstrap aggregating
– Boosting
–…
Outline
• An introduction to the bootstrap
• Bagging: basic concepts (Breiman, 1996)
• Case study: bagging a treebank parser
(Henderson and Brill, ANLP 2000)
Introduction to bootstrap
Motivation
• What’s the average price of house prices?
• From F, get a sample x=(x1, x2, …, xn), and
calculate the average u.
• Question: how reliable is u? What’s the
standard error of u? what’s the confidence
interval?
Solutions
• One possibility: get several samples from
F.
• Problem: it is impossible (or too
expensive) to get multiple samples.
• Solution: bootstrap
The general bootstrap algorithm
Let the original sample be L=(x1,x2,…,xn)
• Repeat B time:
– Generate a sample Lk of size n from L by sampling with
replacement.
– Compute ˆ * for x*.
 Now we end up with bootstrap values
ˆ*  (ˆ1* ,..., ˆB* )
• Use these values for calculating all the quantities of
interest (e.g., standard deviation, confidence intervals)
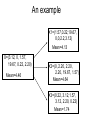
An example
X1=(1.57,0.22,19.67,
0,0,2.2,3.12)
Mean=4.13
X=(3.12, 0, 1.57,
19.67, 0.22, 2.20)
Mean=4.46
X2=(0, 2.20, 2.20,
2.20, 19.67, 1.57)
Mean=4.64
X3=(0.22, 3.12,1.57,
3.12, 2.20, 0.22)
Mean=1.74
A quick view of bootstrapping
• Introduced by Bradley Efron in 1979
• Named from the phrase “to pull oneself up by one’s bootstraps”,
which is widely believed to come from “the Adventures of Baron
Munchausen”.
• Popularized in 1980s due to the introduction of computers in
statistical practice.
• It has a strong mathematical background.
• It is well known as a method for estimating standard errors, bias,
and constructing confidence intervals for parameters.
Bootstrap distribution
• The bootstrap does not replace or add to
the original data.
• We use bootstrap distribution as a way to
estimate the variation in a statistic based
on the original data.
Sampling distribution vs.
bootstrap distribution
• The population: certain unknown
quantities of interest (e.g., mean)
• Multiple samples  sampling distribution
• Bootstrapping:
– One original sample  B bootstrap samples
– B bootstrap samples  bootstrap distribution
• Bootstrap distributions usually approximate the
shape, spread, and bias of the actual sampling
distribution.
• Bootstrap distributions are centered at the value
of the statistic from the original sample plus
any bias.
• The sampling distribution is centered at the
value of the parameter in the population, plus
any bias.
Cases where bootstrap
does not apply
• Small data sets: the original sample is not a
good approximation of the population
• Dirty data: outliers add variability in our
estimates.
• Dependence structures (e.g., time series, spatial
problems): Bootstrap is based on the
assumption of independence.
• …
How many bootstrap samples
are needed?
Choice of B depends on
• Computer availability
• Type of the problem: standard errors,
confidence intervals, …
• Complexity of the problem
Resampling methods
• Boostrap
• Permutation tests
• Jackknife: we ignore one observation at
each time
• …
Bagging: basic concepts
Bagging
• Introduced by Breiman (1996)
• “Bagging” stands for “bootstrap
aggregating”.
• It is an ensemble method: a method of
combining multiple predictors.
Predictors
• Let L be a training set {(xi, yi) | xi in X, yi in Y}, drawn from
the set Λ of possible training sets.
• A predictor Φ: X  Y is a function that for any given x, it
produces y=Φ(x).
• A learning algorithm Ψ: Λ   that given any L in Λ, it
produces a predictor Φ=Ψ(L) in  .
• Types of predictors:
– Classifiers: DTs, DLs, TBLs, …
– Estimators: Regression trees
– Others: parsers
Bagging algorithm
Let the original training data be L
• Repeat B times:
– Get a bootstrap sample Lk from L.
– Train a predictor using Lk.
• Combine B predictors by
– Voting (for classification problem)
– Averaging (for estimation problem)
–…
Bagging decision trees
1. Splitting the data set into training set T1 and test set T2.
2. Bagging using 50 bootstrap samples.
3. Repeat Steps 1-2 100 times, and calculate average
test set misclassification rate.
Bagging regression trees
Bagging with 25 bootstrap samples.
Repeat 100 times.
How many bootstrap samples
are needed?
Bagging decision trees for the waveform task:
• Unbagged rate is 29.0%.
• We are getting most of the improvement using
only 10 bootstrap samples.
Bagging k-nearest neighbor
classifiers
100 bootstrap samples. 100 iterations.
Bagging does not help.
Experiment results
• Bagging works well for “unstable” learning
algorithms.
• Bagging can slightly degrade the
performance of “stable” learning
algorithms.
Learning algorithms
• Unstable learning algorithms: small changes in the
training set result in large changes in predictions.
–
–
–
–
Neural network
Decision tree
Regression tree
Subset selection in linear regression
• Stable learning algorithms:
– K-nearest neighbors
Case study
Experiment settings
• Henderson and Brill ANLP-2000 paper
• Parser: Collins’s Model 2 (1997)
• Training data: sections 01-21
• Test data: Section 23
• Bagging:
• Different ways of combining parsing results
Techniques for combining parsers
(Henderson and Brill, EMNLP-1999)
• Parse hybridization: combining the
substructures of the input parses
– Constituent voting
– Naïve Bayes
• Parser switching: selecting one of the
input parses
– Similarity switching
– Naïve Bayes
Experiment results
Baseline (no bagging): 88.63
Initial (one bag):
88.38
Final (15 bags):
89.17
Training corpus size effects
Summary
• Bootstrap is a resampling method.
• Bagging is directly related to bootstrap.
– It uses bootstrap samples to train multiple predictors.
– Output of predictors are combined by voting or other
methods.
• Experiment results:
– It is effective for unstable learning methods.
– It does not help stable learning methods.
Uncovered issues
• How to determine whether a learning
method is stable or unstable?
• Why bagging works for unstable
algorithms?