Download Lecture21-Measurement

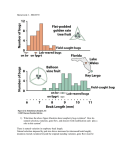
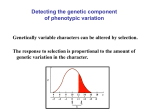
Four Basic Types Of Measurement:
• Categorizing
– Nominal
• Ranking
– Ordinal
• Determination of the size interval
– Interval
• Determination of the size of ratios
– Ratio
CENTRAL TENDENCY AND VARIABILITY (NOMINAL
SCALES)
• Information: guessing game (ESP experiments)
• Background:
- Transmission of signals
- How much is lost in channel?
- How to measure the information transmitted in a
message?
CENTRAL TENDENCY AND VARIABILITY
(NOMINAL SCALES)
One word - no guesses
Two words - one guess
Four words - two guesses
Eight words - three guesses
-# of guesses - power to which two needs to be raised to
define # of words, or log to base 2 of # of alternatives
-Number of guesses called # of bits (binary units)
Varying amounts of
information






Nominal scales:
Name of category does not imply rank,
even if it is a number.
Nominal Scales
• Assignment to categories according to a rule
– e. g., manic - depressive
– paranoid - schizophrenic
– involutional - melancholic
• Starting point of science
–
–
–
–
Chemists - elements
Physicists - atoms and sub-atomic particles
Lineaus - biological categories
Freud - infantile sexuality - neurotic disorders
• Modern Psychology
– does it have reliable units of analysis?
 Reflexes?
 short term memory?
 behavior disorders?
Frequency Distributions
(Nominally Scaled Data)
• Bar graph - histogram
• Mode - summary statistic
y
mode
ordinate
(frequency)
x
abscissa
Ordinal Scales
- Numbers convey relative magnitude.
– rank of one usually assigned to highest magnitude
– can’t add or subtract ranks, e. g., ranks of weight
Rank:
1
2
3
4
5
Weight (lbs.)
200
20
3
2
.5
Ordinal Scales
Summary Statistics:
• Central Tendency: Median (as many
observations above median as below it)
• Variability: Range (difference between the
smallest and highest values)
• Interval scales:
– Size of difference is known
– Units are of equal size
• Ratio scales:
– True zero point exists
– Multiplication or division possible
Magnitude of Psychological Judgments as a
Function of Physical Intensity
CALCULATING THE MEAN
Given the raw data: 2, 4, 6, 8, 10
Mean
=
X
X
•
=
N
2 + 4 + 6 + 8 + 10
=
5
30
=
=6
5
i
Arithmetic Mean = Center of Gravity
Symmetrical Distributions
Measures of Central Tendency in a
Positively Skewed Distribution
Skewed (Asymmetrical) Distributions
Symmetrical Distributions
Asymmetrical Distributions
Binomial Distributions
Calculating Deviations from the Mean
Given the raw data: 2, 4, 6, 8, 10
Mean Deviation
=
Mean Absolute Deviation
=
Variance

Standard Deviation
=
2
=
Calculating Deviations from the Mean
Given the raw data: 2, 4, 6, 8, 10
Mean Deviation
=
Mean Absolute Deviation
=
Variance

Standard Deviation
=
2
=
MEASURING WITH THE STANDARD
DEVIATION: Z-SCORES
Given the raw data: 2, 4, 6, 8, 10
if X 6 and  8
2 6
2 6 44
Z2 Z
2    1
1
. 42. 42
8 8 8 8
8 6
8 6 2 2
Z Z8 8    . .
709709
8 8 8 8
4 6 22
4
6
.
Z4 Z
4    .
709709
8 8 8 8
10
6 4 4
10
6
Z Z10 
  11
. 42. 42
10 
8 8 8 8
CORRELATION
zzx 
rrxy CCzzy

x
y
xy
i
i
i
i
xxy 
xxy

y)
y
r
(
rxyxy ( 
)
y
i
y
i
Normal Distribution
r = +1.0
r = -1.0
+1.0
+1.0
ZZ
yy
Zy
Zy
ZZ
xx
Zx
oror
Zx
Example of Positive Correlation
Examples of Positive, Negative and Minimal
Correlation
QuickTime™ and a TIFF (U ncompressed) decompressor are needed to see this picture.
Relationship between r2 and Predicted Variance
• Example: measures of rainfall and corn height
• Suppose that r = 0.8.
This means that 64% [(0.8)2] of the variance of the
height of corn height is accounted for by knowledge
of how much rain fell.
VALIDITY AND RELIABILITY
• Reliability: To what extent will a test give the same
set of results over repeated measurements?
•Validity: To what extent does a test measure what it
purports to measure?
•Validity and reliability are measured as correlation
coefficients.
Measuring reliability:
• Odd-even or split-half method: To what extent does one half
of the test agree with the items of the second half of the test?
• Test-retest: Results of test is given on two different occasions
are compared. Assumes that there are no practice effects
• Alternative form: Where there is a practice effect, an
alternative form of the original test is given and the results are
compared.
• A reliable test may not be valid.
• A valid test must be reliable may not be valid.
• A valid test must be reliable.
HERITABILITY
• Heritability: The proportion of variance of a
phenotype that is attributable to genetic variance.
• Phenotype: Observable trait
• Genotype: What is transmitted from generation to
generation
• What % of a phenotype is genetic?
• Heritability is calculated by determining phenotypic
variance and the magnitudes of its two components
(genetic and environmental variance)
Calculation of Heritability
Heritability: The proportion of variance of a phenotype that is
attributable to genetic variance.
2p = 2g + 2e
2G
2P
Heritability =
h2
+
2E
2P
=
=
2G
2P
1
(h2 > 0 < 1)
Which Contributes More to Area?
Width or Length
Heritability
Heritability does not
apply to individuals!
Example: h2 of IQ = 0.6. This does not mean
that 60% of an individual’s IQ is genetic and
40% is environmental.
Heritability
Heritability is Specific to the Population in
which it’s Measured
Minimum & maximum values of h (coefficient of
heritability):
2
h2
G
=
2P
(h2 > 0 < 1)
h = 0.00: None of the observed values of phenotype is due
to genes (all of it is due to environmental differences).
h =1.00: All of variance is due to genes.
Examples Of Heritability Coefficients:
•
Piebald Holstein Cow:
h2 = .95 (color)
h2 = .3 (milk production)
•
Pigs:
h2 = .55 (body fat)
h2 = .15 (litter size)
h2 is specific to the environment and population studied.
Heritably estimates are specific to
populations and environments in which
they are measured!
Example 1: Heritability of skin color in Norway and the United
States.
It’s higher in the United States. Why? Because, in Norway the
environment contributes more to phenotypic variation than
family background. In the United States family background
contributes more to variation in skin color then the
environment.
Heritably estimates are specific to
populations and environments in which
they are measured!
Example 2: Heritability of Tuberculosis.
Decreased during the 20th century because of changes in
the environment. Up to and during the 19th century,
everyone who was exposed to germ got sick if they were
susceptible. Improved hygiene made it less likely that
genetically disposed individuals will get TB. Thus, heritability
of TB decreased as environmental diversity increased.
How to Reduce h2
1.
2.
Interbreed - this reduces 2g
Increase 2e.
How to Increase h2
1.
2.
3.
4.
outcrossing - new genes
mutation - new genes
select for rare characteristics
reduce 2e.
QuickTime™ and a TIFF (LZW) decompressor are needed to see this picture.