* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Powerpoint slides
Degrees of freedom (statistics) wikipedia , lookup
History of statistics wikipedia , lookup
Mean field particle methods wikipedia , lookup
Bootstrapping (statistics) wikipedia , lookup
Taylor's law wikipedia , lookup
German tank problem wikipedia , lookup
Regression toward the mean wikipedia , lookup
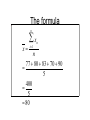
Central Tendency Statistics 2126 Introduction • As useful as like histograms and such are, it would be nice to describe data in terms of Central Tendency • A single number to describe a sample • BTW, the Sample is a subset of the population • We are almost always dealing with samples Back when I was in first year… • 77 80 83 70 90 • Would be nice to describe how I did in first year with a number • Well the one we are all pretty used to is the mean or arithmetic average • The sum of all of the data points, divided by the number of data points The formula n x x i1 n n 77 80 83 70 90 5 400 5 80 The Mean • Sort of a balancing point in the data • Simply adding up the numbers and dividing by the number of observations (n) • X bar is for the sample • We might want to consider my first year marks as a population For a population • The formula does not change, but the symbol does • We use statistics for samples • We use parameters for populations • • The formula is the same really The mean is not mean • In the population, the mean does not change • The sample, yeah it changes, sample to sample • Parameters do NOT CHANGE However, the lecture is getting meaner • If you sample from a population you will get different values for x bar each time • We don’t care about samples in the long run, we care about populations • Calculating is pretty hard, umm it takes forever • Used sometimes, elections, the census Samples vs. populations • A good sample will give you a killer estimate of the population • The census could be done via sampling actually • This is because x bar is an unbiased estimator of • It overestimates as often as it underestimates • Weighted averages sometimes • Some assignments worth more than others for example • There are other measures of central tendency though The median • • • • No need for a formula here 50th percentile Midpoint Half below, half above The mode • • • • • The most common observation Virtually useless Example 25 25 37 42 25 The mode is 25 Tough eh… If…. • If the median = mean = mode we have a unimodal, symmetrical distribution • Say IQ in the population, all measures of central tendency = 100 Normal distribution • You don’t have to get a normal distribution when you have a unimodal, symmetrical distribution • It is probably the most common one though Why? • Why do we need all of these measures of central tendency? • They all have different properties • The mode is useless… • So let’s move on Median vs. the Mean • • • • Say you have five numbers 12345 The mean is 3, as is the median (BTW, the mode is umm well there are 5 of them) • Add another value • 750 Mean vs median in a final all out battle to the death • Now the mean is 127.5 • So adding an extreme value really affects the mean • Median is now umm let’s see • 1 2 3 4 5 750 • 3.5 • cool Median for the win • So sometimes it is good • Think about say union negotiations • Both sides can talk about average salary • Both are right! • In this case the median is more useful So the median is useful • Especially when there are outliers • However you want to leave them in • When you want to take all of the scores into account though you have to use the mean really • All of our techniques are about means • The median is, pretty much, a dead end statistically Running out of pithy titles • The mean is most useful for symmetrical distributions • Most distributions we deal with will be like this • Most are pretty much symmetrical, more or less