Download Ch 1 Lecture 2

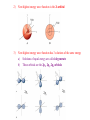
Chapter 1 Structure and Bonding Lecture 2
I.
Lewis Structures: molecular depictions where electrons and bonds are
depicted by dots and pairs of dots
A.
Rules for Drawing Lewis Structures
1) Draw the molecular skeleton after identifying the central atom
2) Count the number of available valence electrons
a) Use periodic table for each atom
b) Add (Cl-) or subtract (NH4+) electrons for charges
3) Fulfill the octet rule for as many atoms as possible
a) Covalent bond = :, double bond = ::, triple bond = :::
b) Electronegative elements can have lone pairs
4) Assign Formal Charge to each atom
a) Formal Charge = (# of valence e-) – (# unshared e-) - ½(shared e-)
b) Place + or – on the appropriate atom
5)
Examples: HBr, NH3, H3O+, CO2, CH4, N2, NO+ (Exercise 1.6)
B.
Exceptions to the Octet Rule
1. Compounds with odd numbers of electrons: CH3, NO
2.
Early second row elements: BeF2, BCl3
**These compounds are very reactive to reach octet: CH3 + CH3, BH3 + H
3.
Third row and higher elements: Valence Shell Expansion:
PCl3, H3PO4, H2SO4
Exercise 1-7
II. Resonance Forms: multiple correct Lewis structures for a given molecule
A.
Example: CO32-
B.
Rules
1) Bracket the set of structures and separate with
2) Only electron pairs move to interconvert; atoms don’t move
Electron Pushing
C.
Resonance Hybrids = The true structure is a mixture of all resonance forms
1. Every resonance form contributes to the overall structure
2. None of the resonance forms are true pictures of the structure
3. The real structure is not interconverting between resonance structures, but
is a composite all of them, all of the time
4. Examples: CO32-, acetate anion, 2-propenyl cation, (Exercise 1-8)
D.
Inequivalent Resonance Forms
1.
Examples: Enolate Anion, Formaldehyde
2.
Major Resonance Contributor = contributes most to the composite
structure
a) Structures with the maximum octets are most important
b) Charges should fit electronegativities
c) Minimize charge separation
d) Examples: NO+, Formaldehyde, Diazomethane, (Exercise 1-9)
Importance
III. Simple Quantum Mechanics: Atomic Orbitals
A.
Classical Mechanics
1) e- is a particle “orbiting” nucleus
2) e- can have any energy (be any distance from the nucleus)
3) Problems
a) e-, n+ would give off energy and eventually “crash” into each other
b) Only certain energies are observed for e- = Energy States
B.
Quantum Mechanics describes e- as a wave
1)
+ and – are not charge
but the sign of the
amplitude
2) “Wave Equations” describe e- movements around nucleus as waves
a) “Wave Functions” (Y) are solutions to the wave equations
b) Y2 = probability of finding e- at each point in space
3) Atomic Orbitals
a) e- locations are quantized, not found everywhere but only at certain
energies
b) 3-D plots of the wave functions indicate where the electron is likely
to be found for the given energy states
4) Wave Equations are very complex, so we can only solve them for simple
systems like H, but the shapes of the atomic orbitals of higher elements
are similar in shape, though larger
C. Shapes of Atomic Orbitals
1) Lowest energy solution
of H wave equation is
called 1s orbital
2)
Next highest energy wave function is the 2s orbital
3)
Next highest energy wave function has 3 solutions of the same energy
a) Solutions of equal energy are called degenerate
b) These orbitals are the 2px, 2py, 2pz orbitals
2px
2py
2pz
4)
D.
Higher energy wave functions give 3s, 3p, 3d, 4s, 4p… orbitals
a) # refers to the energy shell (how far from the nucleus)
b) Letter gives the shape, which is similar but larger for larger shells
Aufbau Principle: adding electrons to the atomic orbitals
1)
Lower energy orbitals are always filled first
2)
Only 2 e- per orbital = Pauli exclusion principle
a) Electron spin = angular momentum of the eb) Paired electrons must have opposite spins
3)
Hund’s rule = degenerate orbitals are occupied equivalently
4)
He, C, Ne, (Exercise 1-11)
5)
Writing Electron configurations: Ar = (1s)2(2s)2(2p)6(3s)2(3p)6