Download x - Yimg

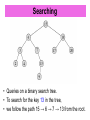
BANHA UNIVERSITY
FACULTY OF COMPUTERS AND INFORMATIC
ALGORITHMS
THIRD YEAR
Lecture six
Dr. Hamdy M. Mousa
Binary search trees
Search trees
• Search trees are data structures that support many
dynamic-set operations,
• Data structures that support many dynamic-set operations.
• Including SEARCH, MINIMUM, MAXIMUM,
PREDECESSOR, SUCCESSOR, INSERT, and DELETE.
• Can be used as both a dictionary and as a priority queue.
• Basic operations take time proportional to the height of the
tree.
• For complete binary tree with n nodes: worst case (lg n).
• For linear chain of n nodes: worst case (n).
• We will cover binary search trees, tree walks, and
operations on binary search trees.
Binary search trees
Binary search trees are an important data structure for
dynamic sets.
• Accomplish many dynamic-set operations in O(h) time,
where h = height of tree.
• we represent a binary tree by a linked data structure in
which each node is an object.
• root[T ] points to the root of tree T .
• Each node contains the fields
• key (and possibly other satellite data).
• left: points to left child.
• right: points to right child.
• p: points to parent. p[root[T ]] = NIL.
• Stored keys must satisfy the binary-search-tree property.
– If y is in left subtree of x, then key[y] ≤ key[x].
– If y is in right subtree of x, then key[y] ≥ key[x].
Draw sample tree
• [This is Figure 12.1(a) from the text, using A, B, D, F, H,
K in place of 2, 3, 5,5, 7, 8, with alphabetic comparisons.
It’s OK to have duplicate keys, though there are none in
this example. Show that the binary-search-tree property
holds.]
• The binary-search-tree property allows us to print out all
the keys in a binary search tree in sorted order by a
simple recursive algorithm, called an inorder tree walk.
• Elements are printed in monotonically increasing order.
How INORDER-TREE-WALK works
•
•
•
•
Check to make sure that x is not NIL.
Recursively, print the keys of the nodes in x’s left subtree.
Print x’s key.
Recursively, print the keys of the nodes in x’s right subtree
• Use the following procedure to print all the elements in
a binary search tree T ,
INORDER-TREE-WALK(x)
if x ≠ NIL
then INORDER-TREE-WALK(left[x])
print key[x]
INORDER-TREE-WALK(right[x])
Theorem
If x is the root of an n-node subtree, then the call
INORDER-TREE-WALK(x) takes  (n) time.
Proof
Let T (n) is the time taken by INORDER-TREE-WALK
when it is called on the root of an n-node subtree.
INORDER-TREE-WALK takes a small, constant amount of
time on an empty subtree (for the test x = NIL), and so
T (0) = c
for some positive constant c.
For n > 0, suppose that INORDER-TREE-WALK is called
on a node x whose left subtree has k nodes and whose
right subtree has n − k − 1 nodes.
The time to perform INORDER-TREE-WALK(x) is
T (n) = T (k)+ T (n −k −1)+d
Substitution method
We use the substitution method to show that T (n)
= (n) by proving that
For n = 0
T (n) = (c + d)n + c
(c + d) . 0 + c = c = T (0).
For n > 0,
T (n) = T (k) + T (n − k − 1) + d
= ((c + d)k + c) + ((c + d)(n − k − 1) + c) + d
= (c + d)n + c − (c + d) + c + d
= (c + d)n + c ,
which completes the proof.
Query ing a binary search tree
• A common operation performed on a
binary search tree is searching for a key
stored in the tree.
• Besides the SEARCH operation, binary
search trees can support such queries as
MINIMUM, MAXIMUM, SUCCESSOR,
and PREDECESSOR.
• In this section, we shall examine these
operations and show that each can be
supported in time O(h) on a binary search
tree of height h.
Searching
• Given a pointer to the root of the tree and a key k,
• TREE-SEARCH returns a pointer to a node with key k
if one exists; otherwise, it returns NIL.
• The procedure begins its search at the root and
traces a path downward in the tree,
TREE-SEARCH(x, k)
if x = NIL or k = key[x]
then return x
if k < key[x]
then return TREE-SEARCH(left[x], k)
else return TREE-SEARCH(right[x], k)
Initial call is TREE-SEARCH(root[T ], k).
Searching
• Queries on a binary search tree.
• To search for the key 13 in the tree,
• we follow the path 15 → 6 → 7 → 13 from the root.
TREE-SEARCH
• The nodes encountered during the recursion form
a path downward from the root of the tree,
• the running time of TREE-SEARCH is O(h),
where h is the height of the tree.
• The same procedure can be written iteratively by
“unrolling” the recursion into a while loop.
• On most computers, this version is more efficient.
ITERATIVE-TREE-SEARCH(x, k)
while x  NIL and k  key[x]
do if k < key[x]
then x ← left[x]
else x ← right[x]
return x
Minimum and maximum
The binary-search-tree property
guarantees that:
– the minimum key of a binary search tree is
located at the leftmost node, and
– the maximum key of a binary search tree is
located at the rightmost node.
Traverse the appropriate pointers (left or
right) until NIL is reached.
Minimum and maximum
TREE-MINIMUM(x)
while left[x]  NIL
do x ← left[x]
return x
TREE-MAXIMUM(x)
while right[x]  NIL
do x ← right[x]
return x
• Time: Both procedures visit nodes that form a
downward path from the root to a leaf.
• Both procedures run in O(h) time, where h is the
height of the tree.
Successor and predecessor
• Assuming that all keys are distinct, the successor of a
node x is the node y such that key[y] is the smallest key
> key[x]. (We can find x’s successor based entirely on
the tree structure. No key comparisons are necessary.) If
x has the largest key in the binary search tree, then we
say that x’s successor is NIL.
There are two cases:
1. If node x has a non-empty right subtree, then x’s
successor is the minimum in x’s right subtree.
2. If node x has an empty right subtree, notice that:
– As long as we move to the left up the tree (move up
through right children), we’re visiting smaller keys.
– x’s successor y is the node that x is the predecessor of
(x is the maximum in y’s left subtree).
Successor and predecessor
TREE-SUCCESSOR(x)
if right[x]  NIL
then return TREE-MINIMUM(right[x])
y ← p[x]
while y  NIL and x = right[y]
do x ← y
y ← p[y]
return y
• TREE-PREDECESSOR is symmetric to TREE-SUCCESSOR.
• Time: For both the TREE-SUCCESSOR and TREEPREDECESSOR procedures, in both cases, we visit nodes on
a path down the tree or up the tree.
• Thus, running time is O(h), where h is the height of the tree.
Example:
•
•
•
•
Find the successor of the node with key value 15. (Answer: Key value 17)
Find the successor of the node with key value 6. (Answer: Key value 7)
Find the successor of the node with key value 4. (Answer: Key value 6)
Find the predecessor of the node with key value 6. (Answer: Key value 4)
Insertion and deletion
• Insertion and deletion allows the dynamic
set represented by a binary search tree to
change.
• The binary-search-tree property must hold
after the change. Insertion is more
straightforward than deletion.
Insertion
• To insert a new value v into a binary
search tree T , we use the procedure
TREEINSERT.
• The procedure is passed a node z for
which key[z] = v, left[z] = NIL, and right[z]
= NIL.
• It modifies T and some of the fields of z in
such a way that z is inserted into an
appropriate position in the tree.
TREE-INSERT procedure
TREE-INSERT(T, z)
y ← NIL
x ← root[T ]
while x = NIL
do y ← x
if key[z] < key[x]
then x ← left[x]
else x ← right[x]
p[z] ← y
if y = NIL
then root[T ] ← z
else if key[z] < key[y]
then left[y] ← z
else right[y] ← z
 Tree T was empty
Example
• Inserting an item with key 13 into a binary search tree.
Lightly shaded nodes indicate the path from the root
down to the position where the item is inserted.
• The dashed line indicates the link in the tree that is
added to insert the item.
Deletion
TREE-DELETE is broken into three cases.
Case 1: z has no children.
– Delete z by making the parent of z point to NIL, instead
of to z.
Case 2: z has one child.
– Delete z by making the parent of z point to z’s child,
instead of to z.
Case 3: z has two children.
– z’s successor y has either no children or one child. (y is
the minimum node-with no left child-in z’s right subtree.)
– Delete y from the tree (via Case 1 or 2).
– Replace z’s key and satellite data with y’s.
z has no children
If z has no children, we just remove it.
z has only one child
If z has only one child, we splice out z.
z has two children
If z has two children, we splice out its successor y, which
has at most one child, and then replace z’s key and
satellite data with y’s key and satellite data.