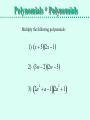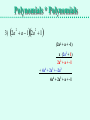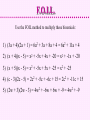Download Use the FOIL Method

Multiplying
Polynomials
Distribute and FOIL
Polynomials * Polynomials
Multiplying a Polynomial by another Polynomial requires
more than one distributing step.
Multiply:
(2a + 7b)(3a + 5b)
Distribute 2a(3a + 5b) and distribute 7b(3a + 5b):
6a2 + 10ab
21ab + 35b2
Then add those products, adding like terms:
6a2 + 10ab + 21ab + 35b2 = 6a2 + 31ab + 35b2
Polynomials * Polynomials
An alternative is to stack the polynomials and do long
multiplication.
(2a + 7b)(3a + 5b)
(2a + 7b)
x (3a + 5b)
Multiply by 5b, then by 3a:
When multiplying by 3a, line
up the first term under 3a.
Add like terms:
(2a + 7b)
x (3a + 5b)
21ab + 35b2
+ 6a2 + 10ab
6a2 + 31ab + 35b2
Polynomials * Polynomials
Multiply the following polynomials:
1) x  52x  1
2) 3w  22w  5
3) 2a  a  12a  1
2
2
Polynomials * Polynomials
1) x  52x  1
(x + 5)
x (2x + -1)
-x + -5
+ 2x2 + 10x
2x2 + 9x + -5
2) 3w  22w  5
(3w + -2)
x (2w + -5)
-15w + 10
+ 6w2 + -4w
6w2 + -19w + 10
Polynomials * Polynomials
3) 2a  a  12a  1
2
2
(2a2 + a + -1)
x (2a2 + 1)
2a2 + a + -1
+ 4a4 + 2a3 + -2a2
4a4 + 2a3 + a + -1
Types of Polynomials
• We have names to classify polynomials based on how
many terms they have:
Monomial: a polynomial with one term
Binomial: a polynomial with two terms
Trinomial: a polynomial with three terms
F.O.I.L.
There is an acronym to help us remember how to multiply
two binomials without stacking them.
(2x + -3)(4x + 5)
F : Multiply the First term in each binomial. 2x • 4x = 8x2
O : Multiply the Outer terms in the binomials. 2x • 5 = 10x
I : Multiply the Inner terms in the binomials. -3 • 4x = -12x
L : Multiply the Last term in each binomial. -3 • 5 = -15
(2x + -3)(4x + 5) = 8x2 + 10x + -12x + -15 = 8x2 + -2x + -15
F.O.I.L.
Use the FOIL method to multiply these binomials:
1) (3a + 4)(2a + 1)
2) (x + 4)(x - 5)
3) (x + 5)(x - 5)
4) (c - 3)(2c - 5)
5) (2w + 3)(2w - 3)
F.O.I.L.
Use the FOIL method to multiply these binomials:
1) (3a + 4)(2a + 1) = 6a2 + 3a + 8a + 4 = 6a2 + 11a + 4
2) (x + 4)(x - 5) = x2 + -5x + 4x + -20 = x2 + -1x + -20
3) (x + 5)(x - 5) = x2 + -5x + 5x + -25 = x2 + -25
4) (c - 3)(2c - 5) = 2c2 + -5c + -6c + 15 = 2c2 + -11c + 15
5) (2w + 3)(2w - 3) = 4w2 + -6w + 6w + -9 = 4w2 + -9