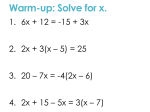Download 2.6 Graphing linear Inequalities in 2 Variables

Graphing Linear Inequalities
in 2 Variables
(B9)
Checking Solutions
• An ordered pair (x,y) is a solution if it
makes the inequality true.
• Are the following solutions to:
• 3x + 2y ≥ 2
• (0,0)
3(0) + 2(0) ≥ 2
0≥2
Not a solution
(2,-1)
3(2) + 2(-1) ≥ 2
4≥2
Is a solution
(0,2)
3(0) + 2(2) ≥ 2
4≥2
Is a solution
To sketch the graph of a linear inequality:
1. Sketch the line given by the corresponding
equation (solid if ≥ or ≤, dashed if < or >).
This line separates the coordinate plane into
2 half-planes.
2. In one half-plane – all of the points are
solutions of the inequality.
In the other half-plane - no point is a solution
3. You can decide whether the points in an entire
half-plane satisfy the inequality by testing
ONE point in the half-plane.
4. Shade the half-plane that has the solutions to
the inequality.
Graphing an Inequality in Two Variables
Graph x < 2
Step 1: Start by
graphing the line x = 2
Now what points
would give you
less than 2?
Since it has to be x < 2
we shade everything to
the left of the line.
Graphing a Linear Inequality
Sketch a graph of y  3
Using What We Know
Sketch a graph of x + y < 3
Step 1: Put into
slope intercept
form
y <-x + 3
Step 2: Graph the
line y = -x + 3
The graph of an inequality is the graph of
all the solutions of the inequality
• 3x+ 2y ≥ 2
• y ≥ -3/2x + 1
(put into slope-intercept form to graph easier)
• Graph the line that is the boundary.
• Before you connect the dots check to see if the
line should be solid or dashed
• solid if ≥ or ≤
• dashed if < or >
y ≥ -3/2x + 1
Step 1: graph
the boundary
(the line is solid ≥)
Step 2: test
a point NOT
On the line
(0,0) is always
The easiest if it’s
Not on the line!!
3(0) + 2(0) ≥ 2
0≥2
Not a solution
So shade the other side of the line!!
Graph: y < 6
y < 3x - 2
4x – 2y < 7