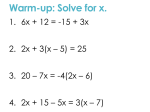* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download 6.5 Graphing Linear Inequalities in Two Variables
Cubic function wikipedia , lookup
Quartic function wikipedia , lookup
Quadratic equation wikipedia , lookup
System of polynomial equations wikipedia , lookup
Elementary algebra wikipedia , lookup
History of algebra wikipedia , lookup
Linear algebra wikipedia , lookup
6.5 Graphing Linear Inequalities in Two Variables Wow, graphing really is fun! Learning Goal #1 for Focus 4 (HS.A-CED.A.2, HS.REI.ID.10 & 12, HS.F-IF.B.6, HS.FIF.C.7, HS.F-LE.A.2): The student will understand that linear relationships can be described using multiple representations. 4 3 2 1 0 In addition to level 3.0 and above and beyond what was taught in class, the student may: · Make connection with other concepts in math · Make connection with other content areas. The student will understand that linear relationships can be described using multiple representations. - Represent and solve equations and inequalities graphically. - Write equations in slope-intercept form, point-slope form, and standard form. - Graph linear equations and inequalities in two variables. - Find x- and yintercepts. The student will be able to: - Calculate slope. - Determine if a point is a solution to an equation. - Graph an equation using a table and slope-intercept form. With help from the teacher, the student has partial success with calculating slope, writing an equation in slopeintercept form, and graphing an equation. Even with help, the student has no success understanding the concept of a linear relationships. What is a linear inequality? • A linear inequality in x and y is an inequality that can be written in one of the following forms. • ax + by < c • ax + by ≤ c • ax + by > c • ax + by ≥ c • An ordered pair (a, b) is a solution of a linear equation in x and y if the inequality is TRUE when a and b are substituted for x and y, respectively. • For example: is (1, 3) a solution of 4x – y < 2? • 4(1) – 3 < 2 • 1 < 2 This is a true statement so (1, 3) is a solution. Check whether the ordered pairs are solutions of 2x - 3y ≥ -2. a. (0, 0) b. (0, 1) c. (2, -1) (x, y) Substitute A (0,0) 2(0) – 3(0) B (0,1) 2(0) – 3(1) C (2,-1) 2(2) – 3(-1) Conclusion = 0 ≥ -2 (0,0) is a solution. = -3 ≥-2 (0, 1) is NOT a solution. = 7 ≥ -2 (2, -1) is a solution. Graph the inequality 2x – 3y ≥ -2 3 2 1 -3 -2 -1 -1 -2 -3 1 2 3 4 Every point in the shaded region is a solution of the inequality and every other point is not a solution. Steps to graphing a linear inequality: 1. Sketch the graph of the corresponding linear equation. 1. Use a dashed line for inequalities with < or >. 2. Use a solid line for inequalities with ≤ or ≥. 3. This separates the coordinate plane into two half planes. 2. Test a point in one of the half planes to find whether it is a solution of the inequality. 3. If the test point is a solution, shade its half plane. If not shade the other half plane. Sketch the graph of 6x + 5y ≥ 30 1. Use x- and yintercepts: (0, 6) & (5, 0) This will be a solid line. 2. Test a point. (0,0) 6(0) + 5(0) ≥ 30 0 ≥ 30 Not a solution. 3. Shade the side that doesn’t include (0,0). 6 4 2 -6 -4 -2 -2 -4 -6 2 4 6 8 Sketch the graph y < 6. 1. This will be a dashed line at y = 6. 2. Test a point. (0,0) 0 < 6 This is a solution. 3. Shade the side that includes (0,0). 6 4 2 -6 -4 -2 -2 -4 -6 2 4 6 8 Sketch the graph of 2x – y ≥ 1 1. Use x- and yintercepts: (0, -1) & (1/2, 0) This will be a solid line. 2. Test a point. (0,0) 2(0) - 0 ≥ 1 0 ≥ 1 Not a solution. 3. Shade the side that doesn’t include (0,0). 3 2 1 -3 -2 -1 -1 -2 -3 1 2 3 4